이어서 노드의 병합과 삭제 과정을 살펴보겠다.
3.노드 병합 및 키 빌려오기
키를 삭제하는 연산을 수행했을 때에도 B-TREE의 속성 중 하나인 '모든 노드는 t(최소차수) - 1개 이상의 키를 가져야 한다.' 를 만족해야 한다. 따라서 삭제연산을 수행하려는 노드의 키의 개수가 t - 1개라면 노드의 키의 개수를 t개 이상으로 늘리는 작업을 해줘야 한다.
이때 노드의 키의 개수를 늘리는 방법은 2가지가 있다.
(1 인접한 형제 노드에서 키를 하나 가져오는 것 또는 (2) 인접한 형제 노드와 병합하는 것이다.
이 둘 중 어떤 방법을 사용하는 지는 형제노드의 키의 개수에 달려있다.
(1)형제노드의 키의 개수가 t개 이상이면 하나를 가져와도 키의 개수가 t - 1개를 만족하기 때문에 키를 가져오는 방법을 택한다.
(2)하지만 형제노드의 키의 개수가 t - 1개라면 키를 하나 가져왔을 때 위에서 말한 키의 최소 개수를 만족하지 못하게 된다. 따라서 두 노드를 병합해준다.
병합을 할 때 부모노드의 키 하나를 가져와 병합을 하게 되는데 병합의 대상이 되는 두 노드의 개수가 각자 t - 1개라 두 노드를 합치고 부모의 키를 하나 가져와도 키의 개수는 총 2t - 1개로 어떤 병합 상황에서도 노드가 가질 수 있는 최대 키의 개수를 넘어가지않는다.
(1)형제 노드에서 키 가져오기
먼저 인접한 형제노드에서 키를 가져오는 코드이다. 이때 왼쪽 형제노드에서 가져올 수도, 오른쪽 형제노드에서 가져올 수도 있다.
형제노드에서 키를 가져올 때는 형제노드의 키를 바로 가져오는 것이 아니라 형제노드에서 가져올 키와 부모노드에서 두 자식의 기준이 되는 키를 바꾸고 , 그 부모노드에서 기준이 되었던 키를 가져온다.
그림으로 나타내면 아래와 같다.
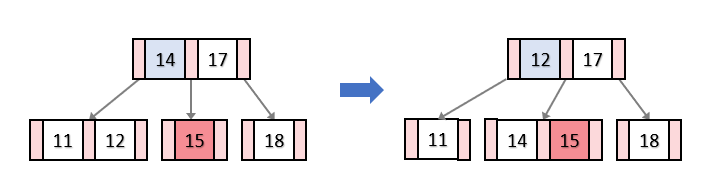
이때 부모의 키를 내리는 이유는 형제의 키를 그대로 가져오면 키를 기준으로 자식을 정렬하는 B-TREE의 성질에 위배되기 때문이다.
아래의 과정에서 형제노드에서 12를 그대로 가져왔다면 14와 17사이의 자식에 12가 들어가게 되므로 B-TREE의 성질에 위배된다.
void move_key_right_to_left(node *left_child, node *right_child, int *parent_key) {
left_child->key[MIN_DEGREE] = *parent_key; //부모의 키를 가져오고
left_child->key_count += 1; //왼쪽 노드의 키의 개수 증가
*parent_key = right_child->key[1]; //부모의 키를 오른쪽 형제노드에서 가져온 키로 바꿔주기
right_child->key_count -= 1; //오른쪽 노드의 키의 개수를 감소
left_child->linker[MIN_DEGREE + 1] = right_child->linker[1];//오른쪽노드에서 자식 가져오기
//오른쪽 노드에서 가장 앞에 있던 키가 없어졌으므로 키와 자식 한칸씩 당겨주기
for (int j = 1; j <= right_child->key_count; j++) {
right_child->key[j] = right_child->key[j + 1];
}
//리프노드이면 자식이 없기 때문에 리프노드가 아닐 때만 자식을 옮겨준다.
if (!left_child->is_leaf) {
for (int j = 1; j <= (right_child->key_count) + 1; j++ ) {
right_child->linker[j] = right_child->linker[j + 1];
}
}
}
void move_key_left_to_right(node *left_child, node *right_child, int *parent_key) {
for (int j = right_child->key_count; j >= 1; j--) {
right_child->key[j + 1] = right_child->key[j];
}
int left_sibling_key_count = left_child->key_count;
if (!right_child->is_leaf){
for (int j = (right_child->key_count) + 1; j >= 1; j--) {
right_child->linker[j + 1] = right_child->linker[j];
}
right_child->linker[1] = left_child->linker[left_sibling_key_count + 1];
}
right_child->key_count += 1;
right_child->key[1] = *parent_key;
*parent_key = left_child->key[left_sibling_key_count];
left_child->key_count -= 1;
}(2)형제 노드와 병합하기
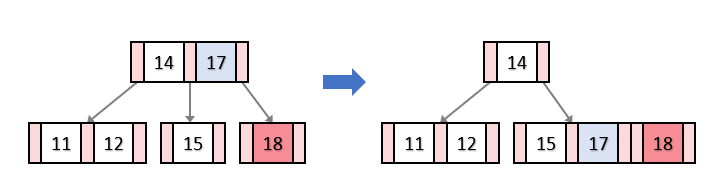
병합을 할 때에는 부모에서 병합할 두 자식을 나누는 기준이 되었던 키를 내려 두 노드와 같이 병합해준다.
이때 부모의 키를 내려주는 것도 B-TREE의 성질을 위배하지 않기 위해서이다.
그림으로 나타내면 아래와 같다.
이때도 부모의 키인 17을 내리지 않고 병합을 했다면 정렬이 제대로 되지도 않고, 부모의 키는 2개인데 자식도 2개가 되어 B-TREE의 성질에 위배된다.
void merge_node(node *parent, node *left_child, node *right_child, int index) {
//왼쪽 자식의 끝에 부모의 키를 내린다.
left_child->key[left_child->key_count + 1] = parent->key[index];
//부모의 키를 내렸으니 부모의 키와 자식을 한칸씩 당겨준다.
for (int j = index; j < parent->key_count; j++) {
parent->key[j] = parent->key[j + 1];
}
for (int j = index + 1; j <= parent->key_count; j++) {
parent->linker[j] = parent->linker[j + 1];
}
parent->key_count -= 1;
//오른쪽 자식의 키를 모두 왼쪽 자식으로 옮겨준다.
for (int j = 1; j <= right_child->key_count; j++) {
left_child->key[MIN_DEGREE + j] = right_child->key[j];
}
if (!left_child->is_leaf) {
for (int j = 1; j <= (right_child->key_count) + 1; j++) {
left_child->linker[MIN_DEGREE + j] = right_child->linker[j];
}
}
//왼쪽 자식의 키의 개수 증가시킨다. 이때 왼쪽자식의 키의 개수는 항상 2t - 1개이다.
left_child->key_count += (right_child->key_count + 1);
//오른쪽 자식은 더이상 사용하지 않기 때문에 메모리를 해제한다.
free(right_child);
}4. 삭제
먼저 삭제 연산의 공통 과정은 아래와 같다.
삭제할 키를 찾아 내려가면서 만나는 노드의 키의 개수가 t - 1개라면 형제노드에서 키를 가져오거나 병합을 해 t개 이상으로 만들어주며 내려간다.
미리 키를 t개 이상으로 만들어주는 이유는 삭제를 진행하고 다시 올라오는 경우의 수를 최대한 줄이기 위해서이다.
예를 들어 삭제를 하는 키가 들어있는 노드의 키의 개수가 t - 1개이고 인접한 형제노드의 키의 개수도 모두 t - 1개라면 삭제를 하기 위해서 병합을 진행해야한다.
하지만 이때 부모노드의 키의 개수도 t - 1개라면 부모노드에서 키를 가져올 수 없기 때문에 다시 부모노드로 올라가 부모노드의 키의 개수를 t개 이상으로 맞춰줘야한다.
따라서 내려올 때부터 만나는 노드들의 키의 개수를 미리 t개 이상으로 맞춰준다면 위 사례처럼 부모노드로 다시 올라가야 하는 경우를 방지할 수 있다.
삭제 연산은 두 가지 경우로 나뉘어 진행된다.
(1)리프노드에서 삭제하는 경우와 (2)내부노드에서 삭제하는 경우이다.
이때 내부노드는 리프노드를 제외한 모든 노드를 말한다.
(1)리프노드에서 삭제하는 경우
리프노드에서 삭제가 이루어질 때는 그냥 키를 삭제하면 된다.
이미 위에서 내려오면서 만나는 모든 노드의 키의 개수를 t개 이상으로 맞춰주기 때문에 바로 삭제를 진행해도 키의 최소개수 t - 1개를 만족하게 된다.
(2)내부노드에서 삭제하는 경우
내부노드에서 삭제를 하는 경우도 왼쪽, 오른쪽 자식노드의 키가 t개 이상일 때와 아닐 때 두 가지로 나뉜다.
(2) - 1 왼쪽 또는 오른쪽 자식 노드의 키가 t개 이상일 때
왼쪽 자식의 키의 개수가 t개 이상이라면 선행키(Inorder Predeccessor), 오른쪽 자식의 키의 개수가 t개 이상이라면 후행키(Inorder Successor) 를 찾아 삭제의 대상이 되는 키에 넣어주고 찾은 선행키, 후행키에 대한 삭제연산을 이어서 진행해준다.
이때 선행키, 후행키는 모두 리프노드에 존재해있다.
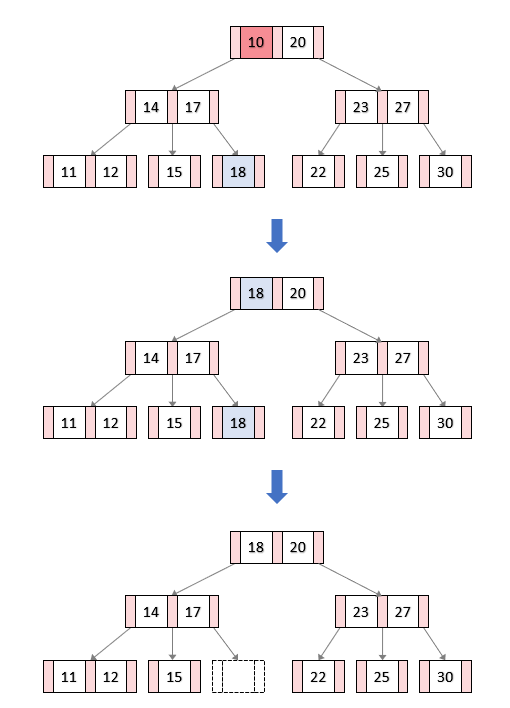
그림으로 나타내면 아래와 같다.
1. 내부노드에서 10을 삭제하기 위해 선행키를 찾아 내려간다. 이때 10의 선행키는 18이고 리프노드에 존재한다.
2. 이어서 10을 18로 바꿔주고 리프노드에 있는 18에 대한 삭제 연산을 진행하면 된다.
이때 선행키와 후행키를 찾는 코드는 아래와 같다.
선행키를 찾기 위해서는 삭제하려는 키의 왼쪽 자식으로 내려간 뒤 리프노드를 만날 때까지 그 노드의 가장 오른쪽의 자식으로 내려간다. 리프노드에 도착했을 때 그 노드에서 가장 큰 키가 선행키가 된다.
후행키를 찾을 때는 내려가는 방향만 정반대고 방법은 동일하다.
int PRED (node *pred_child) {
if (pred_child->is_leaf) {
return pred_child->key[pred_child->key_count];
} else {
return PRED(pred_child->linker[(pred_child->key_count) + 1]);
}
}
int SUCC (node *succ_child) {
if (succ_child->is_leaf) {
return succ_child->key[1];
} else {
return SUCC(succ_child->linker[1]);
}
}(2) - 2 인접한 자식 노드의 키가 모두 t-1개일 때
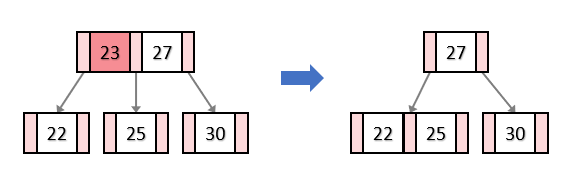
이때는 인접한 자식노드 둘을 병합하고 내부노드의 키를 삭제하면 된다.
그림으로 나타내면 아래와 같다.
아래는 삭제연산을 위한 코드이다.
위에서 설명한 과정을 그대로 진행하되 루트노드의 키가 병합이나 삭제 과정을 통해 모두 사라진다면 루트를 새로 갱신해주는 것만 주의해주면 된다.
void b_tree_delete(node *sub_root, node **root, int k) {
if ((*root)->key_count == 0) {
if ((*root)->is_leaf) {
printf("tree is empty\n");
return;
}
}
node_delete(sub_root, k);
if ((*root)->key_count == 0) {
if ((*root)->is_leaf) {
printf("tree is empty\n");
free(*root);
b_tree_create(root);
return;
}
else {
node *old_root = *root;
*root = (*root)->linker[1];
free(old_root);
return;
}
}
}
void node_delete(node *sub_root, int k) {
if (sub_root->is_leaf){
int original_key_count = sub_root->key_count;
for (int i = 1; i <= sub_root->key_count; i ++) {
if (sub_root->key[i] == k){
for (int j = i; j < sub_root->key_count; j ++) {
sub_root->key[j] = sub_root->key[j + 1];
}
sub_root->key_count -= 1;
}
}
if (original_key_count == sub_root->key_count) {
printf("%d not in b-tree\n", k);
}
return;
}
int i = 1;
while(sub_root->key[i] < k && i <= sub_root->key_count) {
i += 1;
}
if (sub_root->key[i] == k && i <= sub_root->key_count) {
node *left_child = sub_root->linker[i];
node *right_child = sub_root->linker[i + 1];
if (left_child->key_count >= MIN_DEGREE) {
int pred = PRED(left_child);
sub_root->key[i] = pred;
node_delete(left_child, pred);
return;
}
else if (right_child->key_count >= MIN_DEGREE) {
int succ = SUCC(right_child);
sub_root->key[i] = succ;
node_delete(right_child, succ);
return;
} else {
merge_node(sub_root, left_child, right_child, i);
node_delete(left_child, k);
return;
}
return;
}
if (i == sub_root->key_count + 1) {
node *left_child = sub_root->linker[i - 1];
node *right_child = sub_root->linker[i];
if (sub_root->linker[i]->key_count >= MIN_DEGREE) {
node_delete(sub_root->linker[i], k);
return;
}
if (sub_root->linker[i - 1]->key_count >= MIN_DEGREE) {
move_key_left_to_right(left_child, right_child, &(sub_root->key[i - 1]));
node_delete(right_child, k);
return;
}
else {
merge_node(sub_root, left_child, right_child, i - 1);
node_delete(left_child, k);
return;
}
return;
}
else {
node *left_child = sub_root->linker[i];
node *right_child = sub_root->linker[i + 1];
if (sub_root->linker[i]->key_count >= MIN_DEGREE) {
node_delete(sub_root->linker[i], k);
return;
}
if (sub_root->linker[i + 1]->key_count >= MIN_DEGREE) {
move_key_right_to_left(left_child, right_child, &(sub_root->key[i]));
node_delete(left_child, k);
return;
}
else {
merge_node(sub_root, left_child, right_child, i);
node_delete(sub_root->linker[i], k);
return;
}
return;
}
}아래는 구현한 트리를 출력하기 위한 코드이다.
DFS로 구현했다.
void display(node *cur_node, int blanks) {
int i;
if (cur_node->key_count == 0) {
printf("tree is empty\n");
return;
}
if (cur_node->is_leaf) {
for (i = 1; i <= cur_node->key_count; i++) {
for (int j = 1; j <= blanks; j ++)
printf("---!");
printf("%d\n", cur_node->key[i]);
}
return;
}
for (i = 1; i <= cur_node->key_count; i++) {
display(cur_node->linker[i], blanks + 1);
for (int j = 1; j <= blanks; j ++)
printf("---!");
printf("%d\n", cur_node->key[i]);
}
display(cur_node->linker[i], blanks + 1);
return;
}주제가 재밌어 시간가는 줄 모르는 일주일이었다.
피드백 환영합니다.
-끝-
