저번 게시글에 이어서 B-TREE의 연산 과정을 함수와 함께 간단히 보도록 해보자.
1. 노드 구조체 선언
먼저 최소차수를 상수로 선언해준다. 키의 개수나 자식의 개수의 상한과 하한은 최소차수의 영향을 받으므로 자주 쓰게 될 것이다.
이어서 노드 구조체를 선언한다.
구조체는 1. 리프 노드인지 확인하는 bool값 / 2. 키와 자식을 저장할 배열 / 3. 키의 개수
로 이루어져있다.
#define MIN_DEGREE 3
#define MAX_KEY (MIN_DEGREE*2 - 1)
typedef struct _node {
bool is_leaf;
int key[MAX_KEY + 1], key_count;
struct _node *linker[MAX_KEY + 2];
} node;이어서 메인함수, 테스트케이스를 만드는 함수가 있다.
테스트케이스는 0에서 size만큼의 숫자를 생성해 랜덤으로 섞게 되어있다.
노드를 생성할 때 할당된 메모리가 NULL인지 확인하는 node_create 함수로 메모리에 동적 할당이 잘 되었는지 확인한다.
int main() {
node *root;
b_tree_create(&root);
test_case(&root);
display(root, 0);
}
void test_case(node **root, int size) {
int* in_arr = (int*)malloc(sizeof(int) * size);
int* out_arr = (int*)malloc(sizeof(int) * size);
for (int i = 0; i < size; i++) {
in_arr[i] = i;
out_arr[i] = i;
}
for (int i = 0; i < size; i++)
{
int j = i + rand() / (RAND_MAX / (size - i) + 1);
int t = out_arr[j];
in_arr[j] = in_arr[i];
in_arr[i] = t;
}
for (int i = 0; i < size; i++)
{
int j = i + rand() / (RAND_MAX / (size - i) + 1);
int t = out_arr[j];
out_arr[j] = out_arr[i];
out_arr[i] = t;
}
for (int i = 0; i < size; i++) {
int r = in_arr[i];
b_plus_tree_insert(root, r, r * 3);
}
for (int i = 0; i < size; i++) {
int r = out_arr[i];
b_plus_tree_delete(*root, root, r);
}
}
node *node_create() {
node *new_node = (node *)malloc(sizeof(node));
if (new_node == NULL) {
perror("Record creation.");
exit(EXIT_FAILURE);
}
new_node->is_leaf = true;
new_node->key_count = 0;
return new_node;
}
void b_tree_create(node **root) {
node *new_node = node_create();
*root = new_node;
}2. B-TREE 연산
각 노드의 키의 개수가 최대(최소차수 * 2 - 1) 일 때 그 노드에 삽입을 하려 한다면 노드를 두 개로 분할해야하고,
키를 삭제할 때 삭제하는 키가 들어있는 노드의 키의 개수가 키의 최소 개수(최소차수 - 1)개 미만이 된다면 노드를 병합해 키의 최소 개수를 맞춰줘야 한다.
1. 노드 분할
가득찬(키의 개수가 최대인) 노드를 분할할 때에는 가득찬 노드의 중앙의 있는 키를 부모로 올리고 좌우로 2개의 노드로 분할시킨다.
노드를 분할하는 함수는 아래와 같다.
void node_split(node *parent, int child_index) {
node *right_child = (node *)malloc(sizeof(node));
node *left_child = parent->linker[child_index];
right_child->is_leaf = left_child -> is_leaf;
right_child->key_count = MIN_DEGREE - 1;
//중앙키 기준으로 오른쪽의 값을 새로 생성한 노드에 옮겨주기
for (int i = 1; i <= MIN_DEGREE - 1; i ++) {
right_child->key[i] = left_child->key[i + MIN_DEGREE];
}
if (!left_child->is_leaf) {
for (int i = 1; i <= MIN_DEGREE; i++) {
right_child->linker[i] = left_child->linker[i + MIN_DEGREE];
}
}
right_child->linker[0] = parent;
left_child->key_count = MIN_DEGREE - 1;
//부모 키에 자녀 노드의 키의 중앙값이 올라올 자리를 만들기
for (int i = parent->key_count + 1; i >= child_index + 1; i--) {
parent->linker[i + 1] = parent->linker[i];
}
parent->linker[child_index + 1] = right_child;
for (int i = parent->key_count; i >= child_index; i--) {
parent->key[i + 1] = parent->key[i];
}
parent->key[child_index] = left_child->key[MIN_DEGREE]; //꽉찬 노드의 중앙값 올리기
parent->key_count += 1;
}2. 삽입
기본적으로 삽입은 리프노드에서만 진행이 된다. 따라서 루트에서부터 리프노드까지 삽입하려는 값이 들어갈 수 있는 자리를 찾아 내려가야한다.
이때 자리를 찾아 내려가면서 꽉찬 노드를 만난다면 바로 분할을 시켜준다. 그렇게 한다면 삽입이 되는 리프노드는 절대 꽉찬 노드가 되지 않음이 보장되어 하향식으로 한 번에 삽입 연산이 수행 가능하다.
삽입 과정에서 루트노드가 분할이 된다면 루트노드의 중앙값을 키로 갖고 있는 노드가 새로운 루트가 되고 기존의 루트노드는 반으로 갈라져 새로운 루트노드의 자식이 된다.
아래는 삽입 연산 코드이다.
void b_tree_insert(node **root, int k) {
node *curr_root = *root;
//루트를 분할한다면 새로운 루트를 생성
if((*root)->key_count == MAX_KEY) {
node *new_root = node_create();
*root = new_root;
new_root->is_leaf = false;
new_root->linker[1] = curr_root;
curr_root->linker[0] = new_root;
node_split(new_root, 1);
node_insert(new_root, k);
}
else {
node_insert(curr_root, k);
}
}
void node_insert(node *sub_root, int k) {
int i = sub_root->key_count;
//삽입할 자리를 찾는 검색을 수행하는 노드가 리프노드라면 k를 삽입
if (sub_root->is_leaf){
while (i >= 1 && k < sub_root->key[i]) {
sub_root->key[i + 1] = sub_root->key[i];
i -= 1;
}
sub_root->key[i + 1] = k;
sub_root->key_count += 1;
}
// 리프노드가 아니라면 노드의 어느 자식으로 들어가야 올바른 자리를 찾을 수 있는지 검색
// 이때 꽉찬 노드를 만난다면 분할
else {
while (i >= 1 && k < sub_root->key[i]) {
i -= 1;
}
i += 1;
if (sub_root->linker[i]->key_count == MAX_KEY) {
node_split(sub_root, i);
if (k > sub_root->key[i]) {
i += 1;
}
}
node_insert(sub_root->linker[i], k);
}
}아래의 그림은 삽입 과정을 그림으로 나타낸 것이다.
그림에서는 노드의 분할을 내려갈 때 진행하지 않고 삽입을 수행한 후에 진행을 했지만 결과는 같다.
분할이 이루어지지 않는 삽입
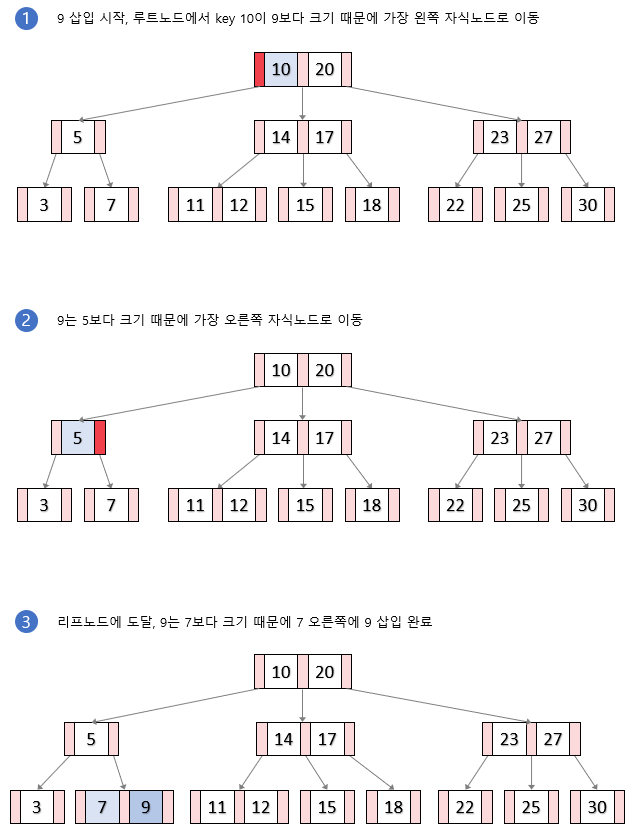
분할이 이루어지는 삽입
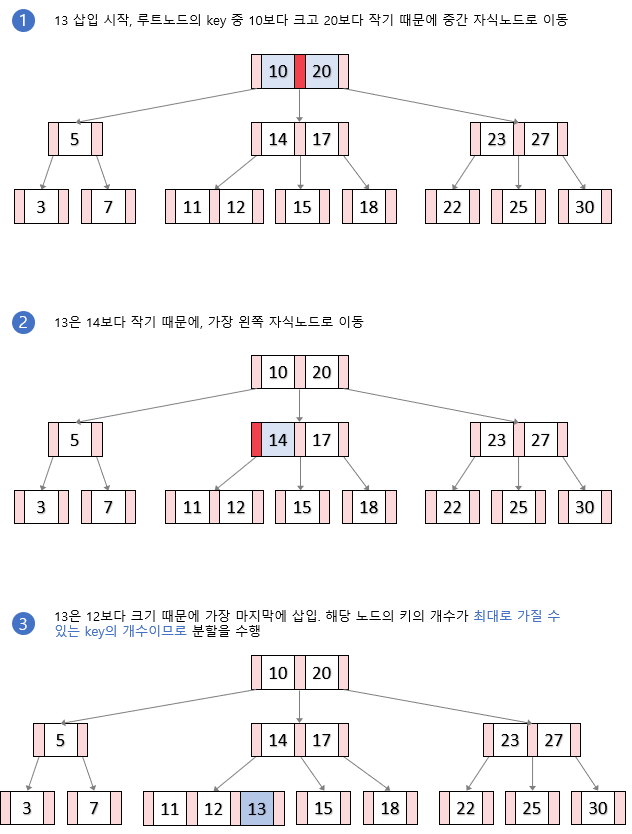
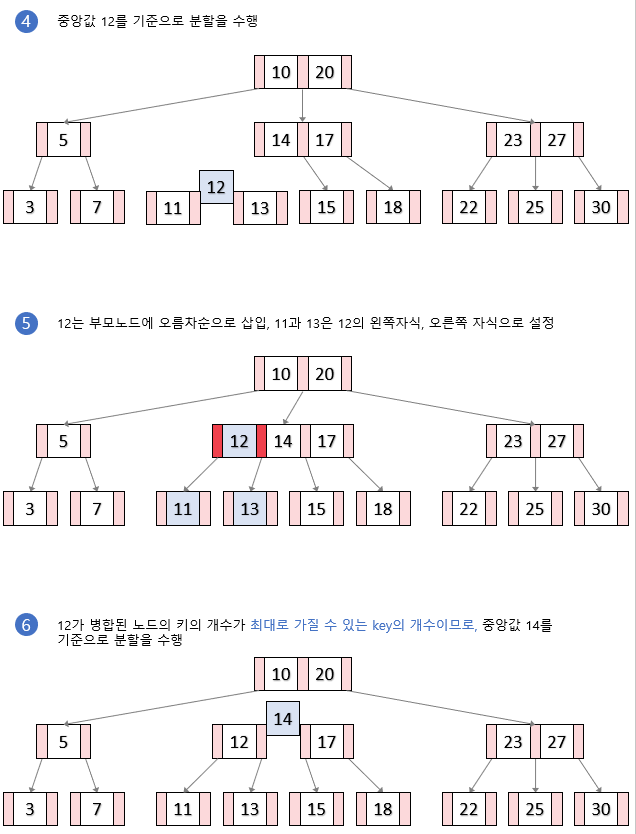
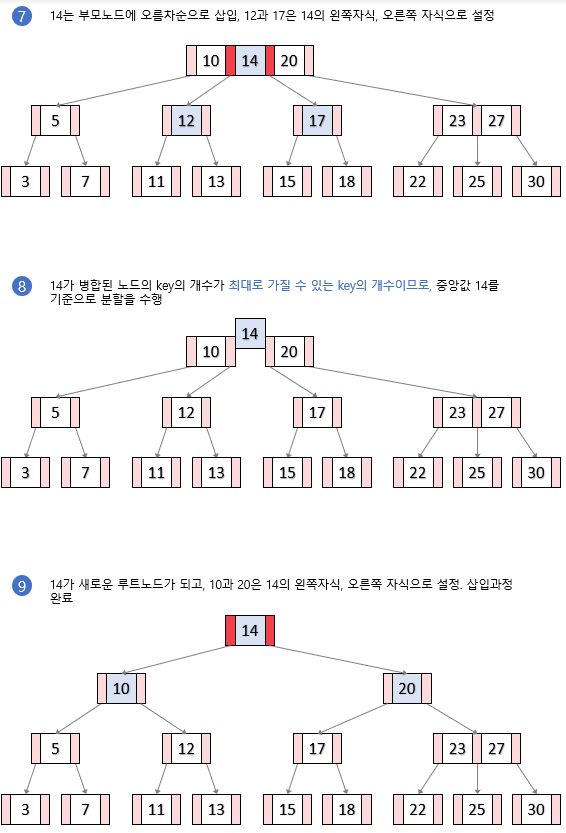
피드백 환영합니다
-끝-
