정규화

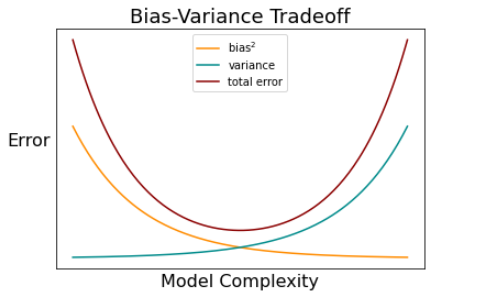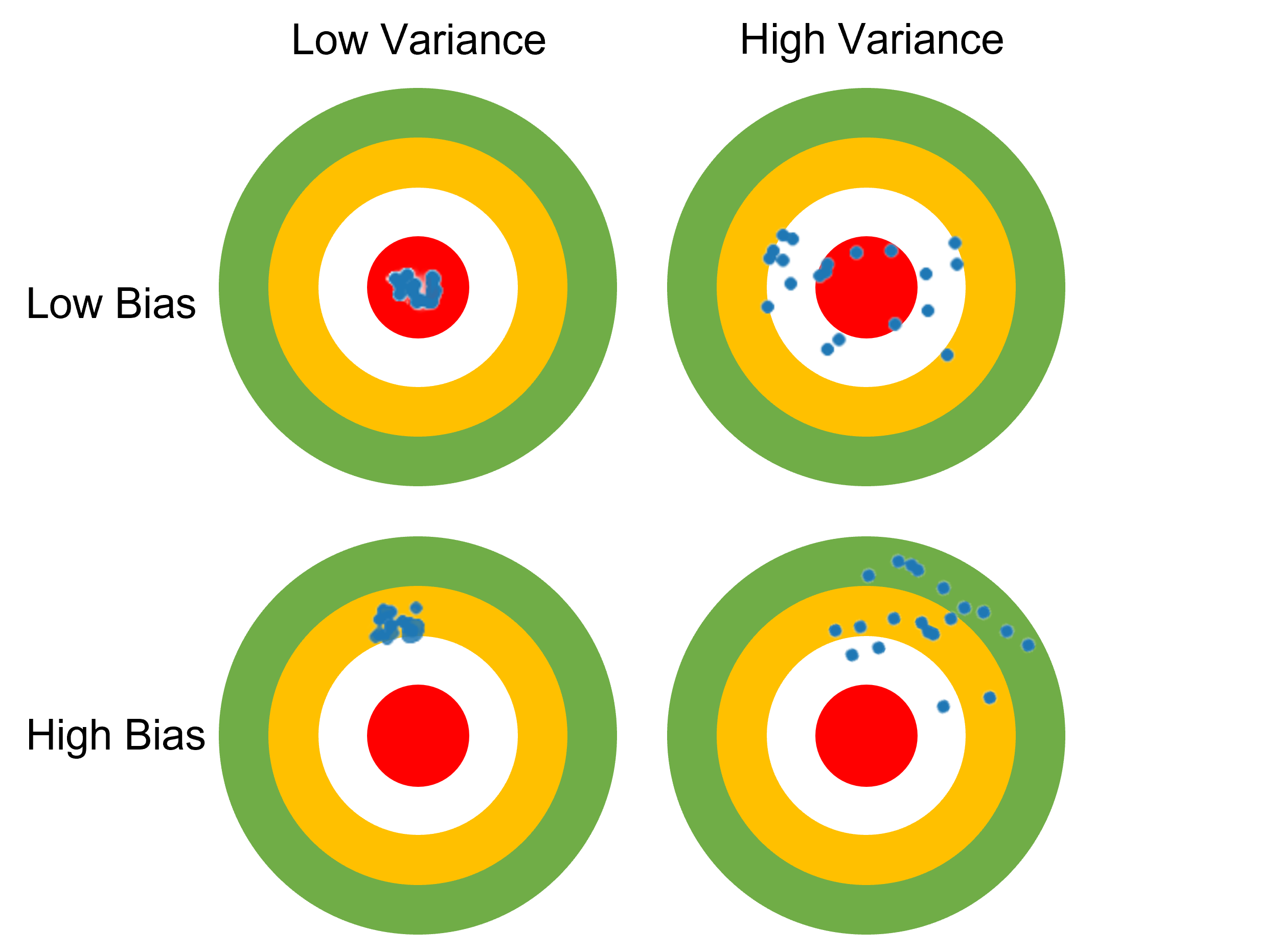
예측값들과 정답이 대체로 멀리 떨어져 있으면 결과의 편향(bias)이 높다고 말하고,
예측값들이 자기들끼리 대체로 멀리 흩어져있으면 결과의 분산(variance)이 높다고 말합니다.

편향(Bias)

• 편향은 예측값들이 정답과 얼마나 떨어져 있는지를 나타낸다.
  • 편향이 높다 = 예측값들이 정답에서 멀다. $\rightarrow$ 데이터를 잘 학습하지 못했다.
  • 편향이 낮다 = 예측값들이 정답에 가깝다. $\rightarrow$ 데이터를 잘 학습했다.
• 모델의 복잡도에 반비례한다.

분산(Variance)

• 예측값들이 서로 얼마나 떨어져있는지를 타나낸다.
  • 분산이 높다 \rightarrow 데이터 셋에 상관없이 일관된 성능을 보여준다.
  • 분산이 낮다 \rightarrow 데이터 셋에 따라 성능이 달라진다.
• 모델의 복잡도$\uparrow \; \rightarrow$ 편향$\downarrow \; \rightarrow$ 분산$\uparrow$

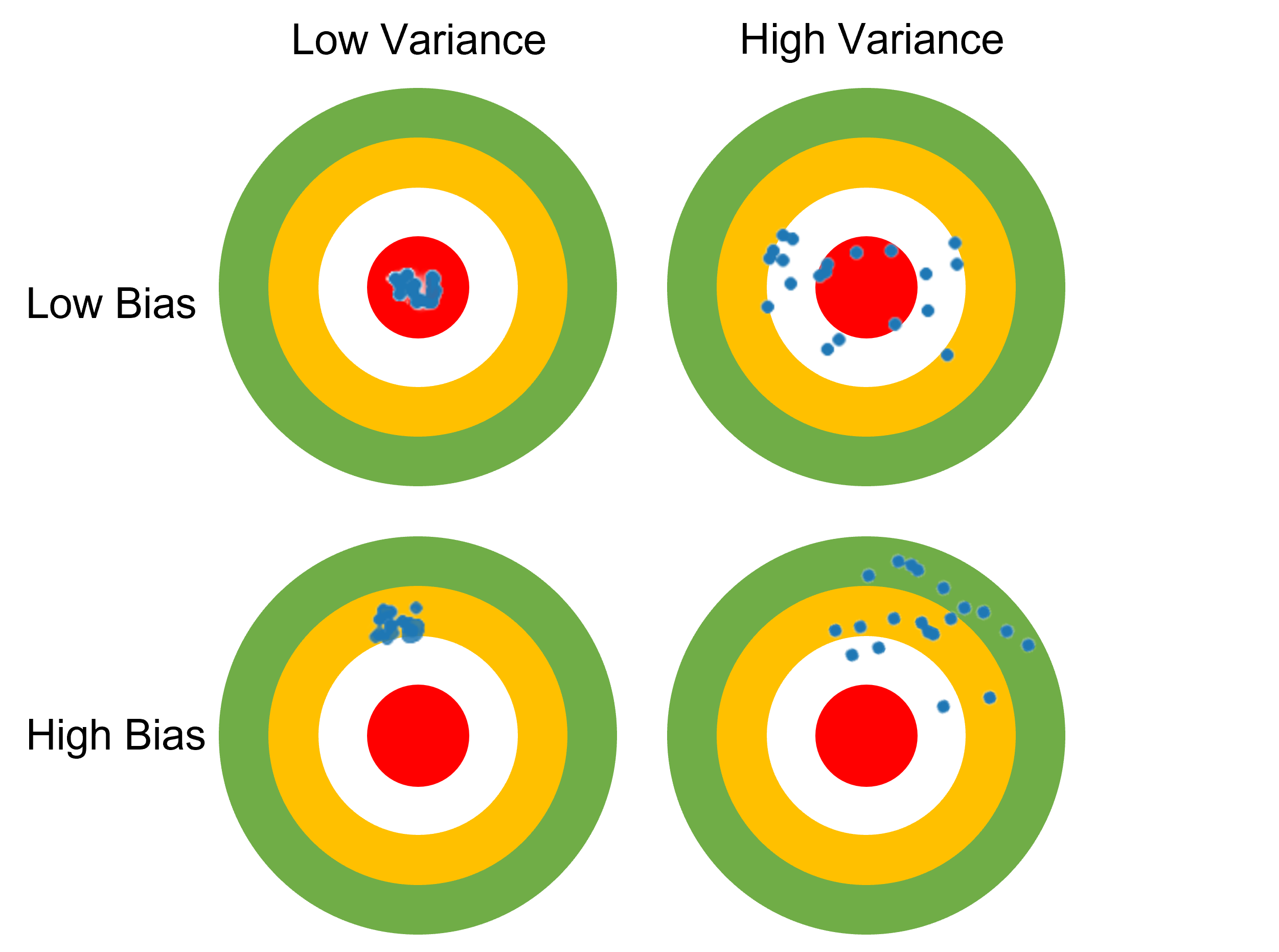
편향-분산 상충관계(Bias-Variance Tradeoff)

• 편향과 분산은 서로 상충관계(Tradeoff) 관계이다.
  • 예: 편향이 커지면 $\rightarrow$ 분산은 감소한다.
• 편향이 크면 $\rightarrow$ 과소적합(Underfitting)
• 분산이 크면 $\rightarrow$ 과대적합(Overfitting)
• 머신 러닝의 성능에 밀접한 관계가 있다.

과소적합(Underfitting)

• 모델이 너무 간단하여 데이터를 잘 학습하지 못하는 현상
  $\rightarrow$ 모델의 복잡도를 높여서 해결한다.
• 보통 편향이 높을 때 발생한다.
• 과적합이라고도 한다.

과대적합(Overfitting)

• 모델이 복잡하여 train 데이터 새로운 데이터(test 데이터)에 대한 성능이 떨어지는 현상
  $\rightarrow$ 모델의 복잡도를 낮춰서 해결한다.
• 보통 분산이 높을 때 발생한다.

머신 러닝 최적화
Underfitting $\leftarrow$ Bestfit $\rightarrow$ Overfitting
머신 러닝 최적화는 곧 Underfitting과 Overfitting의 밸런스, Bestfit을 찾는 과정이라고 볼 수 있다.

정규화(Regularization)

• Overfitting을 방지하는 방법 중 하나
• 가설 함수의 $\theta$값들이 너무 커지는 것을 방지하여 과대적합을 방지하는 방법
• 정규화를 하면 편향$\downarrow$ 분산$\uparrow$
• 손실함수에 $\theta$값들의 절대값을 더한 것을 손실함수로 하여 적용할 수 있다.($\theta$값이 크면 손실함수 값이 커진다.)

단, $\theta_0$은 과대적합과 아무 상관이 없기 때문에 포함하지 않는다.
$\lambda$는 $\theta$값들이 손실함수에 주는 영향을 조절한다.

• $\lambda$가 크면 $\theta$값들을 줄이는 것에 집중
• $\lambda$가 작으면 오차($error$)를 줄이는것에 집중

L1 정규화

• L1 정규화를 적용하는 회귀 모델을 Lasso 모델(Lasso Regression)이라고 한다.
  $\quad\quad\quad\quad\quad\quad\quad\quad\quad J(\theta) = \displaystyle\frac{1}{2m}\sum_{i=1}^m{(h_\theta(x^{(i)})-y^{(i)})^2} + \lambda\sum_{i=1}^n{\vert \theta_i \vert}$

L2 정규화

• L2 정규화를 적용하는 회귀 모델을 Ridge 모델(Ridge Regression)이라고 한다.
  $\quad\quad\quad\quad\quad\quad\quad\quad\quad J(\theta) = \displaystyle\frac{1}{2m}\sum_{i=1}^m{(h_\theta(x^{(i)})-y^{(i)})^2} + \lambda\sum_{i=1}^n{\theta_i^2}$

L1 정규화화 L2 정규화의 차이

• L1 정규화는 모델에 중요하지 않다고 판단되는 $\theta$값들을 0으로 만든다.
• L2 정규화는 $\theta$값들을 0으로 만들지는 않고 조금씩 줄여준다.

L1 정규화는 일부 특성($\theta$)이 배제될 수 있기 떄문에 일반적으로는 L2 규제를 사용한다.

엘라스틱넷(Elastic Net)

• 릿지 회귀와 라쏘 회귀를 절충한 모델
• L1규제와 L2규제를 더해서 사용한다.
• 혼합 정도는 혼합 비율 $r$을 사용해 조절한다.
  • $r$=0 이면 L1 규제
  • $r$=1 이면 L2 규제

조기 종료(Early Stopping)

• 반복적인 학습 알고리즘을 규제하는 방식 중 하나이다. ex) 경사 하강법
• 검증 오차(validation error)가 최솟값에 도달하면 학습을 중지시키는 방법이다.

일반적으로는 검증 오차가 최솟값에 도달했는지 확인하기 어렵기 때문에 보통은 검증 오차가 일정 시간 동안 최솟값보다 클 때 최솟값이라고 판단한다.

이 글은 코드잇 강의를 수강하며 정리한 글입니다. 더 자세한 설명은 코드잇을 참고하세요

코드잇 머신 러닝