본 글은 Hierachical Structure의 글쓰기 방식으로, 글의 전체적인 맥락을 파악하기 쉽도록 작성되었습니다.
또한 본 글은 CSF(Curation Service for Facilitation)로 인용된(참조된) 모든 출처는 생략합니다.

1. Introduction to Neural Networks

---

1.1 CONTENTS

Velog	Lecture	Description	Video	Slide	Pages
작성중	Lecture01	Introduction to Convolutional Neural Networks for Visual Recognition	video	slide	subtitle
작성중	Lecture02	Image Classification	video	slide	subtitle
작성중	Lecture03	Loss Functions and Optimization	video	slide	subtitle
작성중	Lecture04	Introduction to Neural Networks	video	slide	subtitle
작성중	Lecture05	Convolutional Neural Networks	video	slide	subtitle
작성중	Lecture06	Training Neural Networks I	video	slide	subtitle
작성중	Lecture07	Training Neural Networks II	video	slide	subtitle
작성중	Lecture08	Deep Learning Software	video	slide	subtitle
작성중	Lecture09	CNN Architectures	video	slide	subtitle
작성중	Lecture10	Recurrent Neural Networks	video	slide	subtitle
작성중	Lecture11	Detection and Segmentation	video	slide	subtitle
작성중	Lecture12	Visualizing and Understanding	video	slide	subtitle
작성중	Lecture13	Generative Models	video	slide	subtitle
작성중	Lecture14	Deep Reinforcement Learning	video	slide	subtitle
작성중	Lecture15	Invited Talk: Song Han Efficient Methods and Hardware for Deep Learning	video	slide	subtitle
작성중	Lecture16	Invited Talk: Ian Goodfellow Adversarial Examples and Adversarial Training	video	slide	subtitle

1.2 참고 영상

• [핵심 머신러닝 ]뉴럴네트워크모델 1 (구조, 비용함수, 경사하강법)
• [핵심 머신러닝 ] 뉴럴네트워크모델 2 (Backpropagation 알고리즘)

1.3 참고 문서

• Lynn Shin
• 교수님죄송합니다
• Sayer devlog
• 꿈많은사람

1.4 KeyWords

1.4.1 Neural networks

참조 : Neural networks

• 핵심개념
  • 인공신경망은 기계학습과 인지과학에서 생물학의 신경망에서 영감을 얻은 통계학적 학습 알고리즘이다. 인공신경망은 시냅스의 결합으로 네트워크를 형성한 인공 뉴런이 학습을 통해 시냅스의 결합 세기를 변화시켜, 문제 해결 능력을 가지는 모델 전반을 가리킨다.

1.4.2 computational graphs

참조

• computational graphs
• computational graphs
• 핵심개념
  • 계산 과정을 그래프로 나타낸것 여기서 그래프는 복수의 노드(node)와 에지(edge)로 표현
  • 노드를 연결하는 선이 에지

1.4.3 backpropagation

참조 : backpropagation

• 핵심 개념
  • Backpropagation은 오늘 날 Artificial Neural Network를 학습시키기 위한 일반적인 알고리즘 중 하나이다. 한국말로 직역하면 역전파라는 뜻인데, 내가 뽑고자 하는 target값과 실제 모델이 계산한 output이 얼마나 차이가 나는지 구한 후 그 오차값을 다시 뒤로 전파해가면서 각 노드가 가지고 있는 변수들을 갱신하는 알고리즘

1.4.4 biological neurons

참조 : biological neurons

• 핵심 개념
  • 생물학적 뉴런은 활동 전위 또는 스파이크라고하는 약 1 밀리 초 동안 세포막을 가로 질러 날카로운 전기 전위를 생성하는 신경계의 특정 세포

2. Summary

---

2.1 전체 요약

	역전파 및 신경망
전체요약
CNN은 spatial structure를 보존하기 위해 convolutional layer를 사용하는NN의 한 종류이다.(FC레이어는 이미지를 다루기 위해 이미지를 행렬을 한줄로 쭉 펴는 작업(Flatten)를 하는데 이미지에서 붙어있던 픽셀들이 Flatten한 행렬에서는 서로 떨어진다.-> 이미지의 공간적구조(spatial structurw)를 무시한다. 반면에 CNN은 필터를 슬라이드함으로써 주위 픽셀들을 계산하면서 이미지의 공간적인 구조를 보존한다.) Conv 필터(weights)가 입력 이미지를 슬라이딩해서 계산한 값들이 모여 각 출력 Activation map을 만든다. Convolutional layer는 각 레이어 마다 다수의 필터를 사용할 수 있고, 각 필터는 서로 다른 Activation map을 생성한다. 우리는 모든 weights(가중치) 또는 파라미터들의 값을 알고 싶은 것이고, 5강에서는 Optimization을 통해서 네트워크의 파라미터를 학습할 수 있다. 파라미터를 업데이트하면서, Loss라는 산에서 Loss가 줄어드는 방향으로 이동하고 싶어한다. 그렇게 하기 위해서는 gradient의 반대 방향으로 이동하면 된다. Mini-batch stochastic Gradient Desent는 우선 테이터의 일부만 가지고(sample a batch of data) forword pass를 수행한 뒤에 Loss를 계산한다. 그리고 gradient를 계산하기 위해서 backprop를 수행한다.
신경망에서 열심히 훈련시켜놓고 오류나는 것으로 거꾸로 맞춰가면서 변수값을 조정하여 적합한 식을 찾아내는것

2.2 Step #01 : Computational Graph

2.2.1 Gradient Desent(경사하강법)

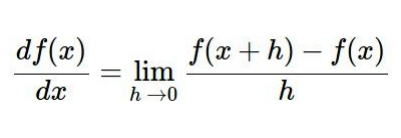
• 수식의 의미 : 기울기 구하는 일반식
• Gradient Desent에는 Numerical Gradient와 Analytic Gradietn가 있다.
• NG는 느리고 대략적인 것을 확인할 수 있지만 쓰기가 편하다
• AG는 빠르고 정확하지만 오류가 발생하기 쉽다.
• 우리는 AG를 찾아 AG를 구현할 것이다.

$cf$.참고

• 특수한 의미의 미적분
  • 미분의 의미
    - 미분(순간변화율)은 어떤 시스템(함수)이 있을 때, 이 시스템이 어떤 변수(요인)에 의해 어떻게 영향을 받는지를 분석하는 가장 핵심적인 도구로 사용
  • 적분의 의미
    - 적분은 입력된 값에 따라 나타난 총 결과, 현상으로 요인에 따른 결과의 상태를 나타냄
• 수학적 Gradient 의미
  • 경사=높이의 변화=스칼라값의 변화율=함수의 미분에 방향=단위벡터를 부여해서, 전체적인 변화의 경향을 나타내는 수학적 방법

2.2.2 Computaional Graph

• 계산을 그래프로 푼다.
• 시작점, 각 체크 포인트와 끝점, 그리고 각 점을 연결하는 선.
• 계산 그래프 이해 단계
  • 1단계
    - 계산 과정을 노드와 화살표로만 표시
    - 노드의 결과값을 오른쪽으로 전달
  • 2단계
    - 노드를 연산으로만 고려
    - 계산 과정의 숫자를 외부 변수로 표시
  • 3단계
    - x, + 등을 넣어 실제 그래프로 계산
• 이 단계에서 Foward, Backward Propagation이 있음
  • Foward Propagation : 계산을 왼쪽에서 오른쪽으로 진행
  • Backward Propagation : 계산을 오른쪽에서 왼쪽으로 진행(cf 편미분)
    

$cf$.참고

• 노드
  • 노드 의미
    - 노드(node)는 컴퓨터 과학에 쓰이는 기초적인 단위이다. 노드는 대형 네트워크에서는 장치나 데이터 지점(data point)을 의미
• 편미분
  • 편미분의 의미
    - dz(높이의 증가량-lim)을 구성하는 각각의 요소의 증가량을 표현할 때 사용하는 것.
    
    

2.2.3 Computational Graph의 사용

• local
  - 전체가 복잡해도 각 노드에서 단순한 계산에 집중에여 문제를 단순화
  - 중간 계산 결과를 모두 보관 가능
  - Backpropagation을 효율적으로 계산이 가능

한줄 이야기

• 계산 과정을 그래프로 나타내는 것

2.3 Step #02 : Backpropagation

2.3.1 Backpropagation 사전이해

• Cost Function = Loss Function
  
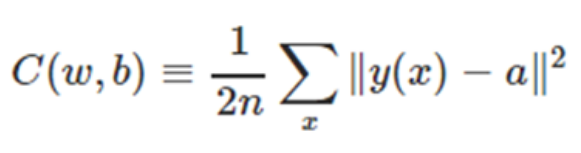
• Cost Function이란 신경망에 훈련데이터 $x$를 가하고
• 실제 출력과 기대 출력간의 차에 대한 MSE(Mean sQuare Error)를 구하는 것
• $y(x)$와 $a$의 차이가 작아질 수록 신경망 학습이 잘 됨
• 훈련데이터를 이용해 가중치($w$)와 바이어스($b$)를 변화시키는 과정을 반복적으로 수행
• Cost Function이 최소값이 되도록 하는 것이 신경망 학습의 목표.

어떻게 w 와 b값을 변화시켜야 최적의 결과를 얻을 수 있을까?

• 참고자료
• w(Weight : 가중치)
  • 다음 노드로 넘어갈때 비중을 조절하는 변수
• b(Bias : 편향)
  • 일종의 성향 버프 : 가중합에 더해주는 상수값
  • 뉴런에서 활성화 함수를 거쳐 최종적으로 출력되는 값을 조절하는 역할

• w나 b를 편미분시키면, 출력 쪽에서 매주 작은 변화가 생기며 선형적인 관계를 확인
• 이 때 출력에서의 오차를 반대 입력 쪽으로 전파시키면서 w, b를 갱신하면 된다.
• Cost Function이 결국 w와 b로 이루어졌기 때문에 출력 부분부터 시작해서 입력쪽으로, 순차적으로cost Function에 대한 편미분을 구하고, 얻은 편미분 값을 이용해 w와 b값을 갱신시킴
• 모든 훈련 데이터에 대해서 이 작업을 반복 수행
• 훈련 데이터에 최적화된 w와 b값을 얻을 수 있다.
• $f(e)$는 sigmoid함수에 해당, e는 각 넷으로부터 입력과 가중치의 곱의 총합
  

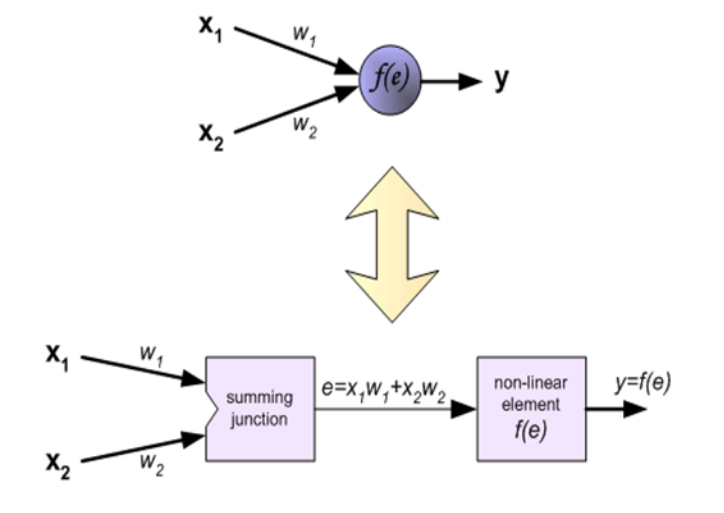
2.3.2 Backpropagation 개념 이해

• 참고자료
• 신경망 변수를 찾기 위한 좋은 방법
• 각 노드가 최종 결과에 어떤 영향을 미치는지 알 수 있음
• 노드에 입력되는 값에 대한 최종 결과의 미분
• 노드의 값이 변했을때 최종결과가 얼마나 변화하는지를 Backpropagation을 통해 구함.
• 편미분을 전달하고 오른쪽에서 왼쪽으로 값을 전달
• 중간까지 구한 미분 결과를 공유할 수 있어서 다수의 미분을 효율적으로 겟나
• 각 변수의 미분을 효율적으로 구할 수 있다.
• 뒤에서 오는 gradients에 local gradient를 곱하는 것으로 해석

$cf$.참고

• Chain Rule
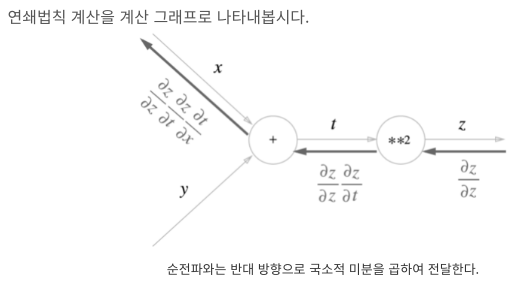
  - 연쇄 법칙
  - 합성함수의 미분에 대한 성질이며, 합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
  - 예 ) $z=(x+y)^2$에서
  $\partial z \over\ \partial x$ = $\partial z \over\ \partial t$$\partial t \over\ \partial x$로 나타낼 수 있다.
  연쇄법칙을 써서 $\partial z \over\ \partial x$를 구하면
  $\partial z \over\ \partial t$ = $2t$
  $\partial t \over\ \partial x$ = 1
  최종적으로 구하고 싶은 $\partial z \over\ \partial x$ 는 두 미분을 곱해 계산
  $\partial z \over\ \partial x$ = $\partial z \over\ \partial t$$\partial t \over\ \partial x$ = $2t* 1 = 2(x+y)$
  

2.3.3 backpropagation의 계산 절차

- 노드로 들어온 입력 신호에 그 노드의 편미분을 곱한 후 다음 노드로 전달
- $\partial z$와 $\partial t$는 전부 소거 되어 '$x$에 대한 $z$의 미분이 됨.
- bckpropagation과 chain rule의 원리가 같음

2.3.4 backpropagation의 핵심을 연쇄법칙의 원리로 설명

- backpropagarion의 계산 절차는 신호 E에 노드의 편미분$\partial y \over\ \partial x$을 곱한 후 다음 노드로 전달.
- 미분값을 효율적으로 구현할 수 있다.

2.3.5 Gate의 종류

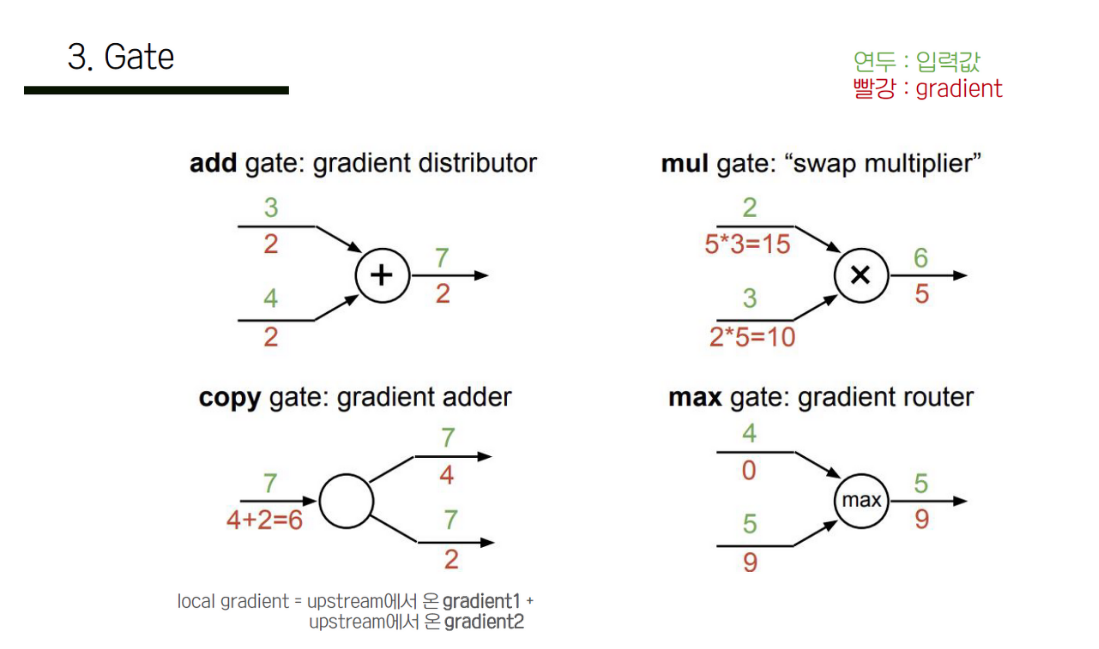
• gate들을 gradient관점에서 보면 distributor, router, switcher로 생각
• add는 x+y로
  • 미분해보면 x방향이든, y방향으로든 1
  • 합성함수 꼴로 나타냈을때 뒤에서 오는 gradient를 앞으로 그대로 전달하는 꼴
  • distributor로 해석
• max는 router인데, max(x,y)인데, 이 둘중 한 값만
  • x가 커서 x가 computational graph에서 forwarding되었다고 하면, 결국 x자체만 뒤에 영향을 끼친것이므로 뒤에서 오는 gradient가 x방향으로만 backwarding
  • backpropagation 입장에서 보면 여러 path중 하나의 path로만 backwarding하는 것
  • router
• mul gate
  • xy일때 x방향으로 들어가는 gradient는 y가 곱해져서 들어감

한줄 이야기

• 학습시킨 후 결과에 따른 오차값을 다시 뒤로 전파해가면서 각 노드가 가지고 있는 변수들을 갱신하는 것
• 뒤에서 오는 gradients에 local gradient를 곱하는 것

2.6 Step #03 : Vectorized Operations & Jacobian Matrix

Gradient가 하나가 아닌 여러 개인 vector 공간에서 backpropagation은?

2.6.1 gradient가 Jacobian matrix가 되는 것

• 다른 계산은 그대로
  
  

한줄 이야기

• 미소 영역에서 ‘비선형 변환’을 ‘선형 변환으로 근사’ 시킨 것
• Vector에 대한 backpropagation은 gradient가 Jacobian Matrix가 됨

2.7 Step #04 : Summary

2.8 지금까지 총정리

• 신경망의 모든 파라미터를 핸들링하는 것은...ㅜㅜ
• 노드의 방향을 앞뒤로 검증할 때 그래프를 유지시켜야..

2.9 Step #05 : Neural Network

• 지금까지 Linear score funtion 을 공부했다.
• 이제는 2-layer Neural Network를 사용한다.
  $f = W_2max (0,W_1x)$ 같은
  이것이 3layer로 ->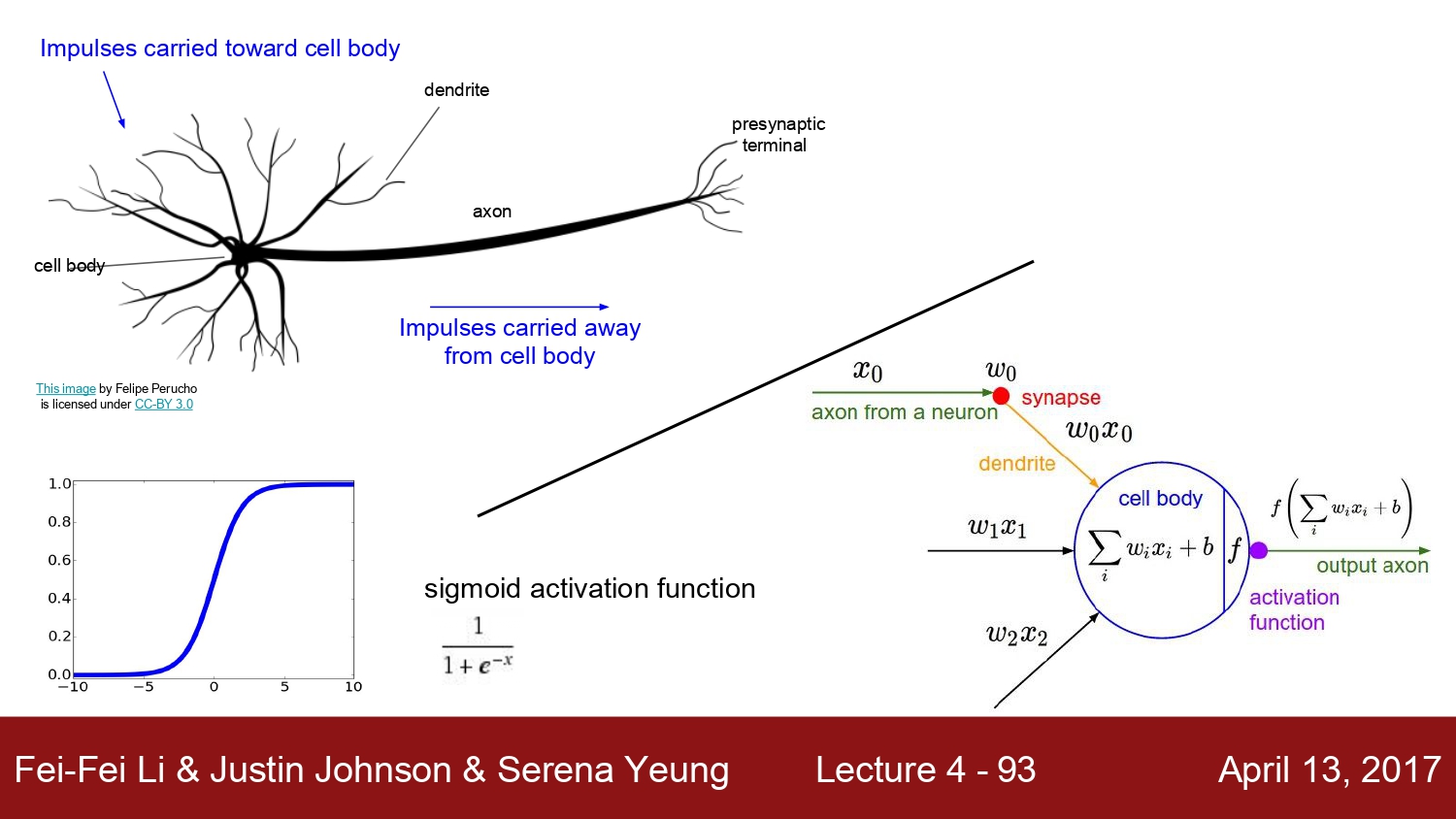 $f = W_3max(0,W_2max (0,W_1x))$
  다양한 비선형 함수를 사용하여 인간의 신경망을 따라갈 수 있는 모델을 만든다.
  
  

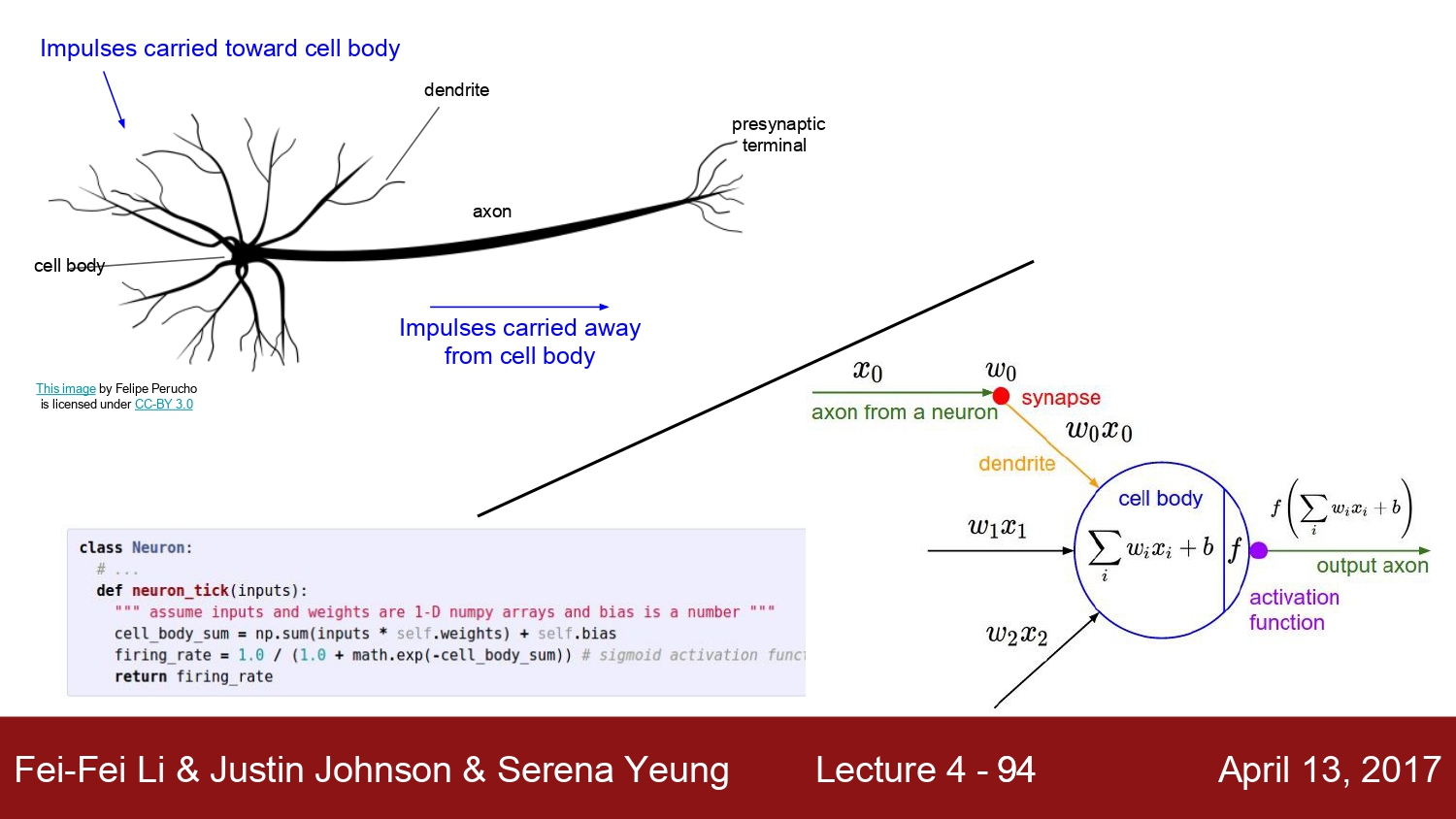
한줄 이야기

• 생물학적 뉴런은 인공 신경망보다 복잡한 구조로 인공신경망과 일대일 대응은 아니다.