영상 내용 정리
0. 기본 용어
정렬: 데이터를 특정한 기준에 따라 순서대로 나열하는 것- 데이터 간의 대소관계를 정의할 수 있어야 함
- 데이터의 크기 순서가 유의미한 정보여야 함
정렬 알고리즘: 데이터의 특성과 크기에 맞게 효율적으로 정렬하는 방법
1. 유명한 정렬 알고리즘
선택 정렬- 아이디어
남아있는 데이터 중 i 번째 최소값을 선택해서 정렬하는 방법
- 아이디어
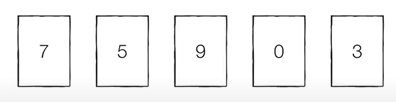
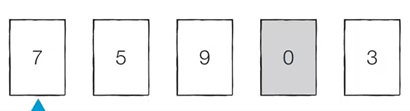
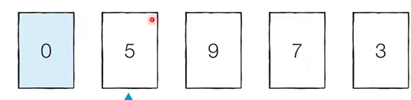
- 코드
A <- 우리가 정렬하고 싶은 array, 크기는 N
for i in range(len(A)):
min_ind = i # i번째 최소값을 찾는 걸 목표로 함.
for j in range(i+1, len(A)):
if A[min_ind] > A[j]:
min_ind = j # 최소값의 ind 업데이트
A[i], A[min_ind] = A[min_ind], A[i] # 최소값과 i번째 원소를 스왑
print(*A)- 성능
- 평균 시간 복잡도 : O(N^2) (쌩으로 for 문 두 번 돌리기 때문)
- 공간 복잡도 : O(N) (주어진 Array 외에 다른 저장 공간 안 씀) - 특징
- 아이디어는 간단하나 다른 정렬 알고리즘에 비해 느림 삽입 정렬- 아이디어
처리되지 않은 데이터를 하나씩 적절한 위치에 삽입하는 방법
(처리되지 않은 데이터를 처리된 데이터 하나 하나와 비교하면서 처리된 데이터 중에 적절한 위치에 삽입하는 방법)
- 아이디어
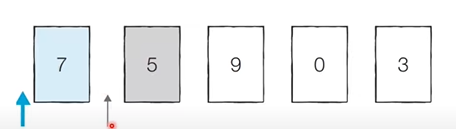
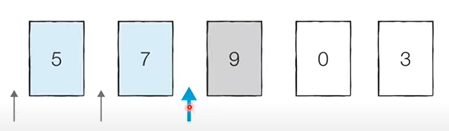
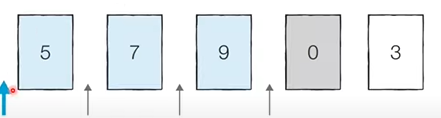
- **코드**
```python
A <- 우리가 정렬하고 싶은 array, 크기는 N
for i in range(1, len(A)):
for j in reversed(range(1, i+1)):
if A[j] < A[j-1]:
A[j], A[j-1] = A[j-1], A[j]
else: break
print(*A)
```
- **성능**
- 평균 시간 복잡도 : O(N^2)
- 공간 복잡도 : O(N) (주어진 Array 외에 다른 저장 공간 안 씀)
- **특징**
- 데이터가 거의 정렬되어 있을 때는 가장 빠름퀵 정렬-
배경지식
분할정복법: 큰 문제를 작은 문제들로 나눠서 풀고, 그 결과를 모아서 큰 문제를 푸는 방법
-
아이디어
기준 데이터(pivot)을 기준으로 큰 데이터와 작은 데이터들을 계속 분할하고, 분할한 데이터를 정렬한 다음 모아서 전체 데이터를 정렬하는 방법
(큰 데이터와 작은 데이터를 분할하는 방법 : (1) 왼쪽에서부터 pivot보다 큰 데이터를, 오른쪽에서부터 작은 데이터를 찾는다. (2) 데이터를 서로 스왑해서 정배열이 되게 한다. 이때 데이터들이 정배열일 경우 작은 데이터를 pivot과 대신 스왑한다. (3) pivot과 작은 값이 스왑되면 왼쪽은 pivot보다 작은 데이터, 오른쪽은 큰 데이터로 분할되었다는 말이므로 재귀를 건다.) -
예시
2 3 0 5 1 7 2 3 0 5 1 7 2 1 0 5 3 7 0 1 2 5 3 7 0 1 5 3 7 3 5 7 0 1 2 3 5 7 -
코드
A <- 우리가 정렬하고 싶은 array, 크기는 N def quick_sort(A, st, end): # 분할한 데이터가 하나면 return if start >= end: return # pivot 설정 pivot = start left = start + 1 right = end # 1. 데이터 분할 while left <= right: # pivot이 작은 값과 교체될 때까지 # pivot 보다 큰 값을 왼쪽에서 순서대로 찾는다. while left <= end and A[left] <= A[pivot]: left += 1 # while이 끝나고 나온 left 값은 pivot 보다 크거나 end # 비슷하게 pivot 보다 작은 값을 오른쪽에서 순서대로 찾는다. while right > start and A[right] >= A[pivot]: right -= 1 # 순서가 정배열이 아니면 큰 값 작은 값 스왑 if left < right : A[left], A[right] = A[right], A[left] else: # 아니면 pivot과 작은 값 교체 A[pivot], A[right] = A[right], A[pivot] # 2. 분할한 데이터에 재귀 quick_sort(A, start, right - 1) quick_sort(A, right + 1, end) quick_sort(A, 0, N-1) print(*A) -
성능
- 평균 시간 복잡도 : O(NlogN) (pivot 설정 잘못하면 O(N^2))
- 그래서 C++ STL에서는 처음, 중간, 마지막 값의 median을 pivot으로 사용
- 공간 복잡도 : O(N) (주어진 Array 외에 다른 저장 공간 안 씀)
- 평균 시간 복잡도 : O(NlogN) (pivot 설정 잘못하면 O(N^2))
-
특징
- 대부분의 경우에 가장 적합하고 빠름
-
계수 정렬(Counting sort)-
아이디어
데이터가 정수형이고 크기가 제한되어 있다고 할 때, 각 데이터를 Counting하고 Counting된 만큼 데이터를 반복하여 정렬하는 방법| 2 | 3 | 2 | 3 | 1 | | --- | --- | --- | --- | --- | | 1 | 2 | 3 | | --- | --- | --- | | 1 | 2 | 2 | **결과 : 1 2 2 3 3** -
코드
A <- 우리가 정렬하고 싶은 array, 크기는 N 논의의 편의를 위해 0 ~ K인 정수라고 가정 count = [0] * (K+1) # Counting for i in range(len(A)): count[A[i]] += 1 # Counting한 만큼 반복 출력 for i, cnt in enumerate(count): for _ in range(cnt): print(i, end = ' ') -
성능
- 평균 시간 복잡도 : O(N + K) (K는 출력)
- 공간 복잡도 : O(N + K) (K는 저장하는 리스트)
-
비고
- 데이터의 크기나 자릿수에 대한 제한은 유의미한 정보
- 1/100 의 소숫점 2번째 자리 vs sqrt(3.32)의 소숫점 2번째 자리
- 데이터의 크기나 자릿수에 대한 제한은 유의미한 정보
-
➕ 팀 정렬(Tim sort)
- 파이썬 built-in sort 함수가 쓰는 알고리즘
병합 정렬+삽입 정렬- 최악의 경우에도 시간 복잡도 O(nlogn)와 공간 복잡도 O(n)을 보장해줌
💯 코테 문제 풀이
영상 속 예시 문제


# 아이디어
# (1) : 수를 바꿔서 A의 총합이 늘어나려면 A의 값이 B의 값보다 작아야 한다.
# (2) : 한 번 바꿀 때 제일 좋은 방법은 A에서 제일 작은 값을 B에서 제일 큰 값으로 바꾸는 것이다.
import sys
N, K = map(int, sys.stdin.readline().rstrip().split())
A = list(map(int, sys.stdin.readline().rstrip().split()))
B = list(map(int, sys.stdin.readline().rstrip().split()))
A.sort()
B.sort(reverse = True)
for i in range(K):
# (1) : 수를 바꿔서 A의 총합이 늘어나려면 A의 값이 B의 값보다 작아야 한다.
if A[i] < B[i]:
A[i], B[i] = B[i], A[i]
else: break
print(sum(A))1181 단어 정렬 (실버 5)
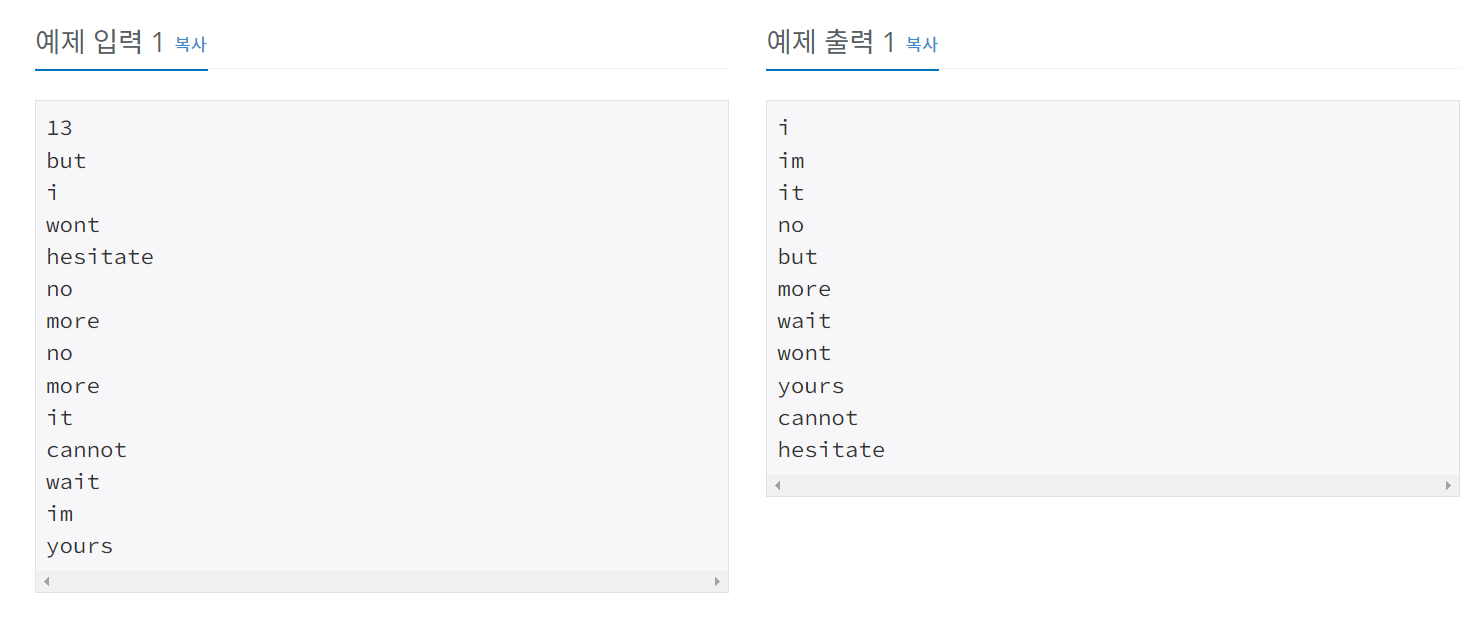
"""
알파벳 소문자로 이루어진 N개의 단어가 들어오면 아래와 같은 조건에 따라
정렬하는 프로그램을 작성하시오.
길이가 짧은 것부터
길이가 같으면 사전 순으로
단, 중복된 단어는 하나만 남기고 제거해야 한다.
"""
"""
첫째 줄에 단어의 개수 N이 주어진다. (1 ≤ N ≤ 20,000)
둘째 줄부터 N개의 줄에 걸쳐 알파벳 소문자로 이루어진 단어가 한 줄에 하나씩 주어진다.
주어지는 문자열의 길이는 50을 넘지 않는다.
"""
import sys
inp = sys.stdin.readlines()
N = int(sys.stdin.readline().rstrip())
# 일단 set으로 받고 list로 다시 바꿈
strings = list({sys.stdin.readline().rstrip() for _ in range(N)})
# python built-in sort 함수는 튜플을 키로 받았을 경우 튜플의 원소 순서를 기준으로 정렬
# 따라서 (len(x), x) 이면 먼저 길이로 정렬하고 x로 정렬함
strings.sort(key = lambda x : (len(x), x))
for string in strings: print(string)