그래프 이론(DSU, 위상 정렬) + 프로그래머스 Lv4

https://youtu.be/aOhhNFTIeFI

영상 내용 정리

0. 기본 용어

• 서로소 : 어떤 두 집합이 서로 공통 원소가 없으면, 두 집합을 서로소 관계라고 함
• 서로소 집합 자료구조 : 서로소인 집합들로 나누어진 데이터를 처리하기 위해 쓰이는 자료구조
  • Disjoint Set Union, Union-Find 등 이름이 여러가지임
  • 보통 노드를 key로 가지는 테이블로 구현됨

1. DSU의 기본 연산

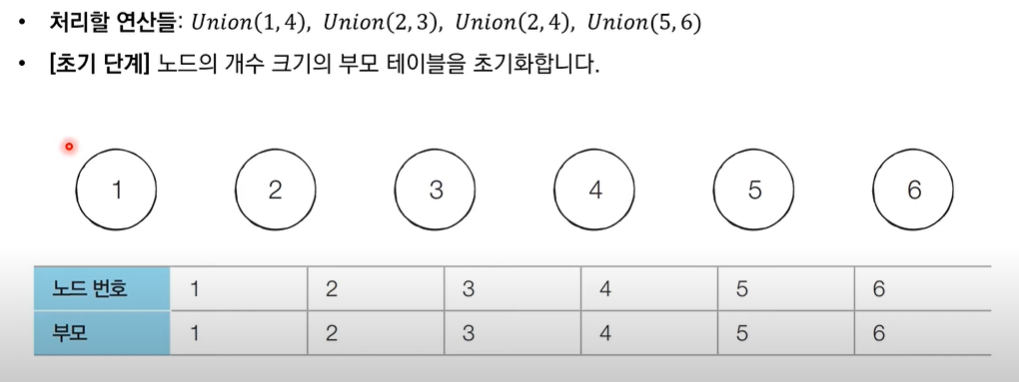
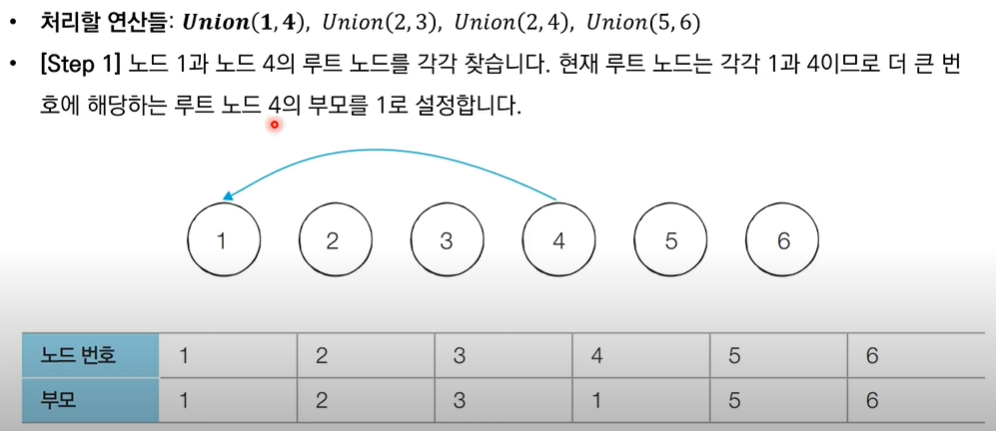
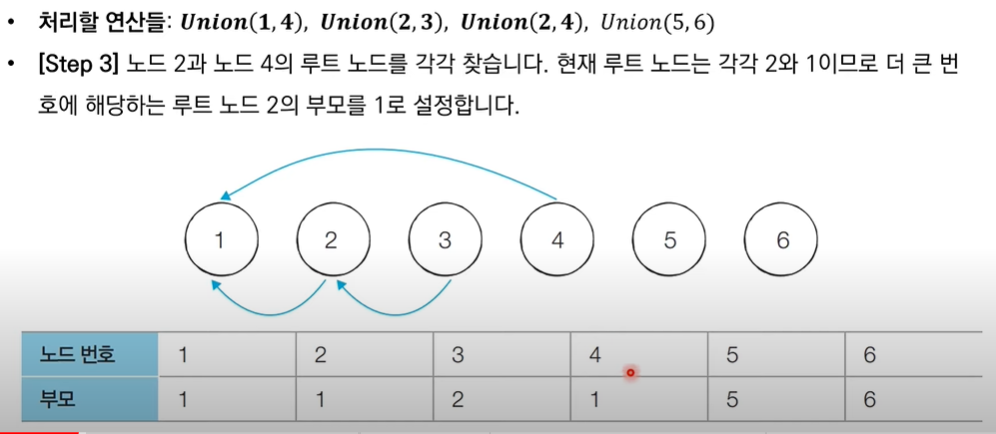
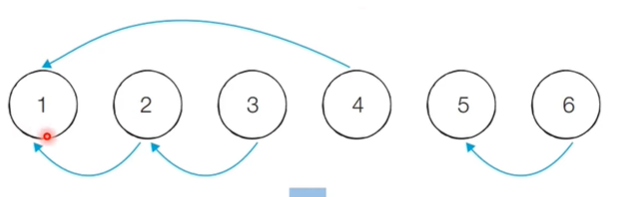
• Union(v1, v2) : v1과 v2가 포함되어 있는 집합들을 하나의 집합으로 합치는 연산
  • 예 : {1, 2, 3} {4, 5, 6} → Union(1, 4) → {1, 2, 3, 4, 5, 6}
• Find(v1) : v1이 속한 집합이 어떤 집합인지 알려주는 연산 ( 그 기준은 보통 root 노드 )
  • 예 : 1 → 2 → 3, {1, 2, 3} 이면 find(2)은 1을 반환
• 예시

2. 구현

# 1. Root 노드를 저장할 parent 초기화
parent = [ i for i in range(V + 1) ]

# 2. Root 노드를 찾을 find_parent 함수 정의
# 재귀적으로 root 함수를 찾는다.
def find_parent(parent, v):
		# v의 root는 자기자신이므로 root 노드는 이 조건문을 건너뛰고 자기 자신을 return
		if v != parent[v]:
				parent[v] = find_parent(parent, parent[v]) # root가 아닌 경우, 재귀 호출
		return parent[v]

# 3. 두 노드가 포함된 집합을 하나로 합칠 union 함수 정의
def union(parent, v1, v2):
		r1 = find_parent(parent, v1)
		r2 = find_parent(parent, v2)
		# 두 집합을 합칠 때 어느 쪽 root를 공통 root로 선택하는지는 정해져있지 않다.
		# 강의 영상에서는 간단히 root 번호가 작은 순서대로 설정함
		if r1 < r2:
				parent[r2] = r1
		else:
				parent[r1] = r2

3. DSU 가 쓰이는 알고리즘

• 무방향 그래프에서 사이클 판별

  • 아이디어

    • E(v1, v2)가 주어졌을 때, 이 v1과 v2가 기존에 연결되어 있으면 사이클이 생기고 없으면 생기지 않는다.
      • 기존에 연결되어 있으면 == ‘find_parent(v1) == find_parent(v2)’

  • 코드

    
    V, E <- V : 노드, E : 그래프에 있는 모든 Edge
    
    # parent 초기화
    parent = [ i for i in range(V + 1) ]
    
    # 위의 두 함수 구현
    def find_parent ...
    def union ... 
    
    cycle = False
    
    for edge in E:
    		v1, v2 = edge
    		# v1과 v2가 기존에 연결되어 있는지 확인
    		if find_parent(parent, v1) == find_parent(parent, v2):
    				cycle = True
    				break
    		# 아닌 경우 union
    		else: union(parent, v1, v2)
    
    print(cycle)

• 최소 신장 트리 찾기(크루스칼 알고리즘)

  • 용어

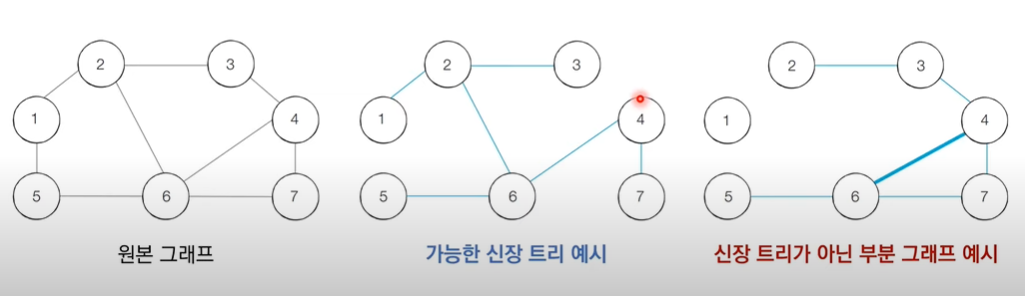
    • 신장 트리(Spanning Tree) : 그래프의 모든 노드를 포함되어 서로 연결되면서, 사이클은 없는 부분 그래프
    • 최소 신장 트리 : Edge의 weight(or 거리, 비용 …) 총합이 최소인 신장 트리
      

  • 아이디어

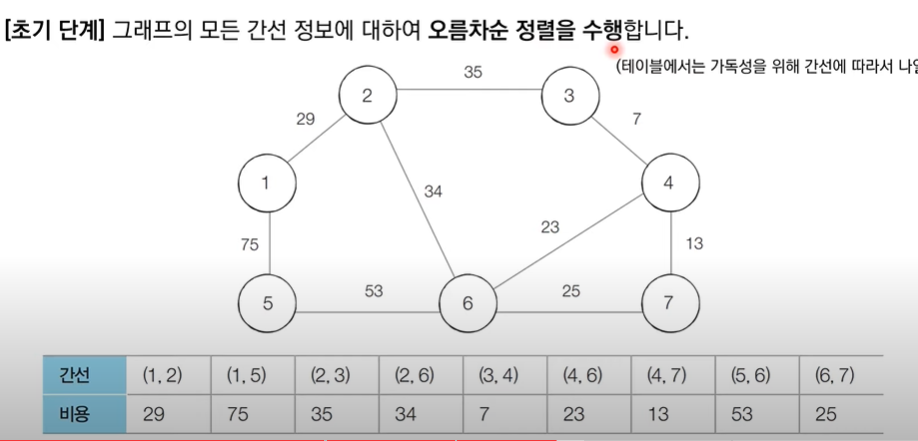
    • Edge를 정렬해서 작은 순서대로 트리에 포함시키자
      

  • 코드

    V, E <- V : 노드, E : 그래프에 있는 모든 Edge
    
    # parent 초기화
    parent = [ i for i in range(V + 1) ]
    # E 정렬
    E.sort(key = lambda x : x.weight)
    
    # 위의 두 함수 구현
    def find_parent ...
    def union ... 
    
    result = 0
    for edge in E:
    		v1, v2 = edge
    		weight = edge.weight
    		# 사이클을 만들지 않는 경우에만 union
    		if find_parent(parent, v1) != find_parent(parent, v2):
    				union(parent, v1, v2)
    				result += weight
    		
    print(result)

4. 위상 정렬

• 비순환 방향 그래프에서 위상 정렬

  • 용어
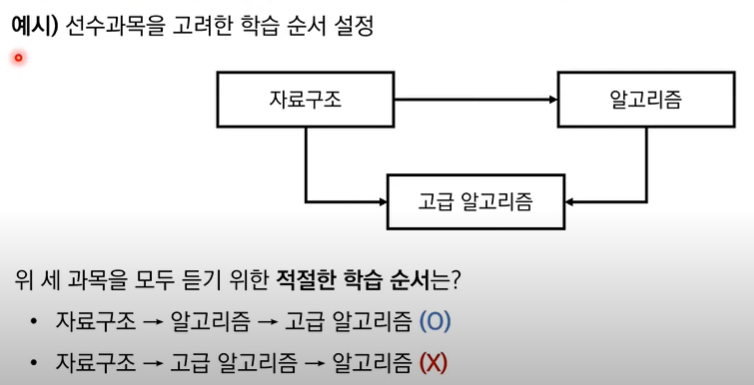
    - 위상 정렬 : 모든 노드를 방향성에 거스르지 않도록 나열하는 것
    - 진입차수 = 특정 노드로 들어오는 간선의 갯수
    - 진출차수 = 특정 노드에서 나가는 간선의 갯수
    

  • 아이디어

    • 순서상 제일 앞에 있는 노드들은 진입차수가 무조건 0이어야 한다
    • 그 노드들을 제거했을 때 제일 앞에 있는 노드는 똑같이 진입차수가 0이어야 한다
    • 따라서 진입차수가 0인 노드를 차례대로 출력하면 그게 위상 정렬 순서다

  • 코드

    from collections import deque
    
    V, E <- V : 노드, E : 그래프에 있는 모든 Edge
    
    # graph 초기화
    graph = [ [] for i in range(V + 1) ]
    # 진입차수 기록
    indegree = [ 0 for i in range(V + 1) ]
    for edge in E:
    		v1, v2 = edge
    		graph[v1].append(v2) # graph에 edge 업데이트
    		indegree[v2] += 1 # v2의 진입차수 1 증가
    
    result = []
    # 선입선출해야 하므로 queue 사용
    q = deque()
    for i in range(1, V+1):
    		# 진입차수 0인 노드부터 시작
    		if indegree[i] == 0:
    				q.append(i)
    
    while q:
    		v = q.popleft()
    		result.append(v)
    		for i in graph[v]:
    				indegree[i] -= 1
    				# 진입차수 0이면 추가
    				if indegree[i] == 0:
    						q.append(i)
    
    print(*result)

  • 특징

    • 한 노드에서 복수의 노드로 진출할 경우, 위상 정렬 결과는 여러개로 존재함
    • 모든 노드를 방문하기 전에 큐가 빈다면 사이클이 존재
    • DFS를 통한 구현도 가능

💯 코테 문제 풀이

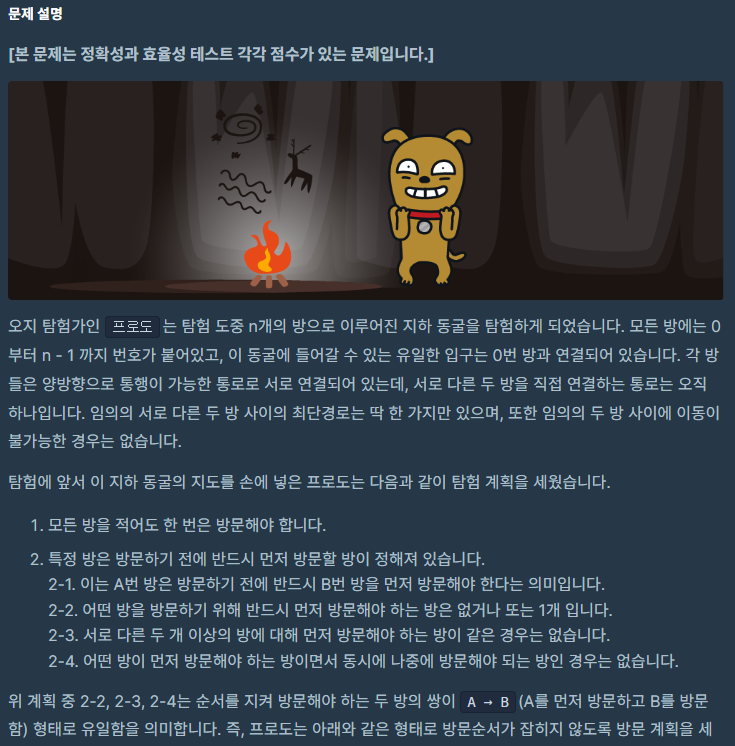
프로그래머스 동굴 탐험 (Lv.4) - 위상정렬

문제 링크

	
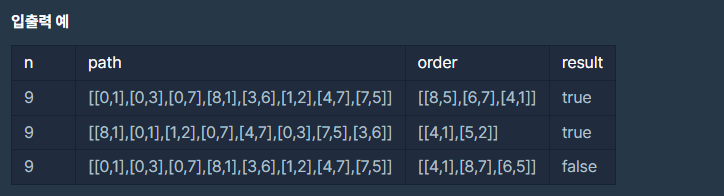
  from collections import deque

   def solution(n, path, order):
       """
       이 문제가 위상정렬이랑 연관이 있는 이유:
           시작 지점이 0으로 고정되어 있으므로, 
           처음 노드를 방문할 때는 노드 간의 방향성이 어느 정도 존재한다.
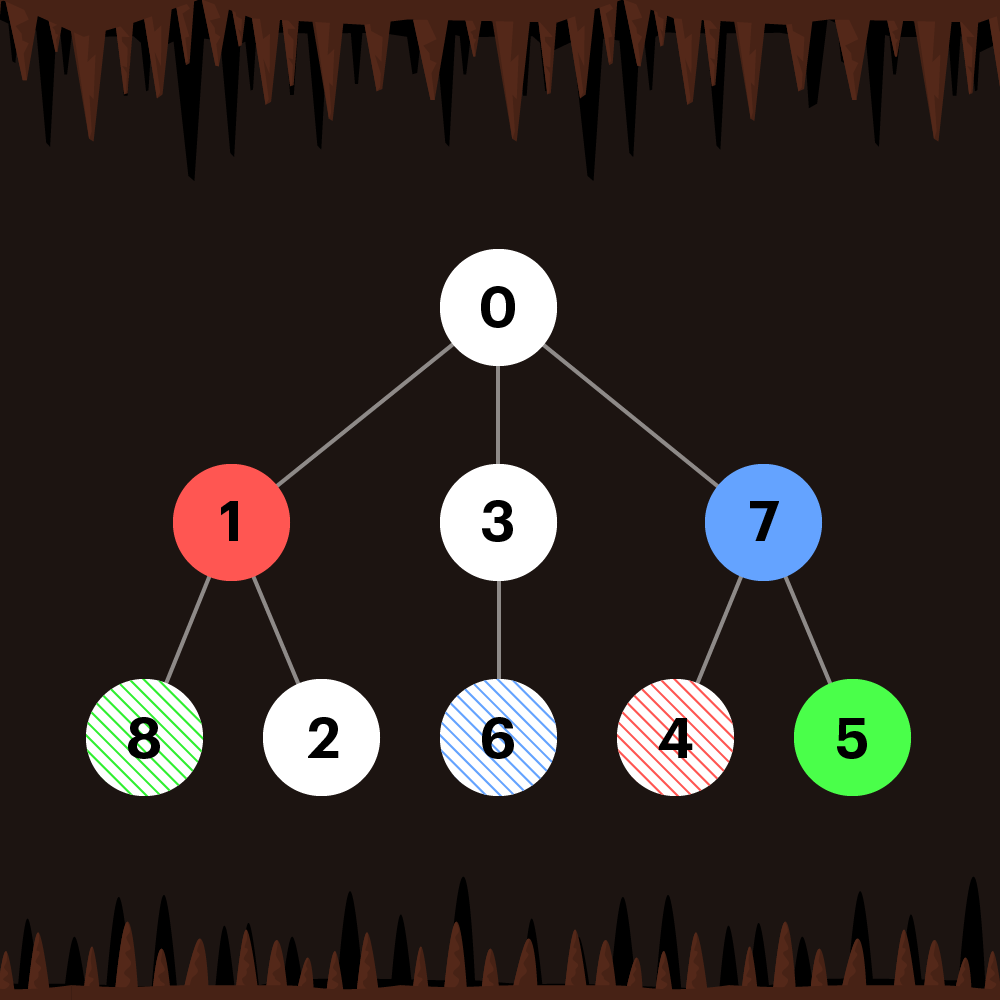
           예를 들어 그림 1을 보면 노드 8로 가는 과정에서 1을 거치지 않는 것은 불가능하다.
           즉, 8은 절대로 1보다 먼저 진입차수가 0이 될 수 없다. 따라서 order에서 (8, 1)이 
           포함되어 있다면 답은 False가 된다.

           이런 맥락에서 어떤 노드 v1의 진입차수가 0이 되려면
           1) v1의 부모 노드 중 하나 이상이 진입차수가 먼저 0이 되어야 하고
           2) order에서 v1보다 먼저 나와야 하는 노드 또한 진입차수가 먼저 0이 되어야 한다.
           따라서 indegree를 두 개 만들어서 동시에 0이 되었는지 여부로 queue에 추가하면 된다.

           만일 답이 오답이라면, 즉 방향 위상이 서로 모순된다면 둘 중 하나의 조건이 만족되지 않으므로,
           모든 노드를 거치지 못하고 정렬이 정지될 것이다.
     """

     # 먼저 그래프를 초기화
     graph = [[] for i in range(n)]
     for p in path: 
         v1, v2 = p
         graph[v1].append(v2)
         graph[v2].append(v1)

     # indegree 두 개 초기화
     idg1 = [0 for i in range(n)]
     idg2 = [True for i in range(n)]
     idg1[0] = idg2[0] = True # 0은 root이므로 True

     # v1 -> v2, 
     # 다음으로 order를 테이블 형태로 초기화
     after = [0 for i in range(n)]
     for o in order:
         v1, v2 = o
         if v2 == 0: return False # 테스트 케이스 하나가 인자가 2개임...
         after[v1] = v2
         idg2[v2] = False

     q = deque()
     q.append(0)
     visited = [0 for _ in range(n)]
     visited[0] = 1
     count = 1
     while q:
         v = q.popleft()
         idg2[after[v]] = True

         for i in graph[v]:
             idg1[i] = True
             if idg1[i] and idg2[i] and not visited[i]:
                 q.append(i)
                 visited[i] = 1
                 count += 1
                 # print(i)

         # order에 대한 순서도 사실상 edge와 같으므로
         i = after[v]
         if idg1[i] and not visited[i]:
             q.append(i)
             visited[i] = 1
             count += 1
             # print(i)

     # print(count, n)
     return count == n
   ```