Multimodal Learning with Transformers: A Survey

오늘 리뷰할 논문은 transformer 관련 Multimodal Learning (MML) survey다.

포스트는 리뷰보다는 메모 형식이다.

---

• 논문의 구성은 다음과 같다.
  (1) a background of multimodal learning, Transformer ecosystem, and the multimodal big data era,
  (2) a theoretical review of Vanilla Transformer, Vision Transformer, and multimodal Transformers, from a geometrically topological perspective,
  (3) a review of multimodal Transformer applications, via two important paradigms, i.e., for multimodal pretraining and for specific multimodal tasks,
  (4) a summary of the common challenges and designs shared by the multimodal Transformer models and applications
  (5) a discussion of open problems and potential research directions for the community.

Further, learning per-modal specificity and inter-modal correlation can be simply realized by controlling the input pattern of self-attention.

• The major features of this survey include
  (1) We highlight that Transformers have the advantage that they can work in a modality-agnostic way. Thus, they are compatible with various modalities (and combinations of modalities). To support this view, we, for the first time, offer an understanding of the intrinsic traits of Transformers in a multimodal context from a geometrically topological perspective. We suggest that self-attention be treated as a graph style modelling, which models the input sequence (both uni-modal and multimodal) as a fully-connected graph. Specifically, self-attention models the embedding of arbitrary tokens from an arbitrary modality as a graph node.
  (2) We discuss the key components of Transformers in a multimodal context as mathematically as possible.
  (3) Based on Transformers, cross-modal interactions (e.g., fusion, alignment) are essentially processed by self-attention and its variants. In this paper, we extract the mathematical essence and formulations of Transformer based MML practices, from the perspective of self-attention designs.

• main contribution
  (1) We present a theoretical reviewing of Vanilla Transformer, Vision Transformer, and multimodal Transformers, from a geometrically topological perspective.
  (2) We contribute a taxonomy for Transformer based MML from two complementary perspectives, i.e., application based and challenge based. In Section 4, we provide a review of multimodal Transformer applications, via two important paradigms, i.e., for multimodal pretraining and for specific multimodal tasks. In Section 5, we summarize the common challenges and designs shared by the various multimodal Transformer models and applications.
  (3) We discuss current bottlenecks, existing problems, and potential research directions for Transformer based MML.

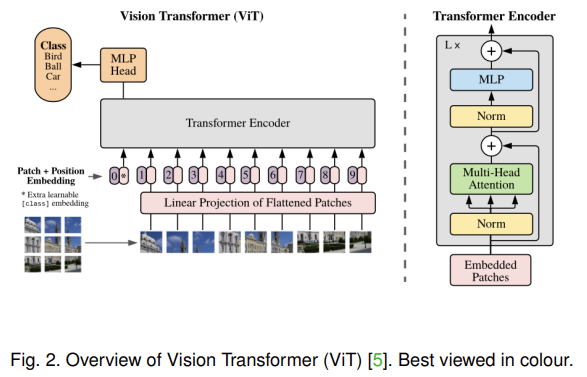
• ViT
  Vision Transformer (ViT) [5] is a seminal work that contributes an end-to-end solution by applying the encoder of Transformer to images.

VideoBERT [7] is a breakthrough work that is the first work to extend Transformer to the multimodal tasks. Following VideoBERT, a lot of Transformer based multimodal pretraining models (e.g., ViLBERT [107], LXMERT [108], LXMERT [108], VisualBERT [109], VL-BERT [110], UNITER [111], CBT [112], Unicoder-VL [113], B2T2 [114], VLP [115], 12-in-1 [116], Oscar [117], Pixel-BERT [118], ActBERT [119], ImageBERT [120], HERO [121], UniVL [122]) have become research topics of increasing interest in the field of machine learning.

• CLIP [123]
  It is a new milestone that uses multimodal pretraining to convert classification as a retrieval task that enables the pretrained models to tackle zero-shot recognition. Thus, CLIP is a successful practice that makes full use of large-scale multimodal pretraining to enable zero-shot learning. Recently, the idea of CLIP is further studied, e.g., CLIP pretrained model based zero-shot semantic segmentation [124], ALIGN [125], CLIP-TD [126].

• Multimodal dataset 설명한 부분도 있는데 생략

We highlight that Vanilla Transformers can be understood from a geometrically topological perspective [164], because due to the self-attention mechanism, given each tokenized input from any modalities, Vanilla self-attention (Transformer) can model it as a fully-connected graph in topological geometry space [165].

Compared with other deep networks (for instance, CNN is restricted in the aligned grid spaces/matrices), Transformers intrinsically have a more general and flexible modelling space.

Each block has two sub-layers, i.e., a multi-head self-attention (MHSA) layer and a position-wise fully-connected feed-forward network (FFN). To help the back propagation of the gradient, both MHSA and FFN use Residual Connection followed by normalization layer.

• normalization을 projection 전/후에 하는 것 중 어느게 나은지 연구가 필요하다고 한다. 원본 논문은 post-normalization을 했는데 수학적으로는 pre-normalization이 낫다고 한다.

• Position Embedding은 Vanilla transformer은 sin/cos 함수를 썼다. 최근엔 다양한 구현이 나오고 있다.

• Position Embedding Discussion
  How to understand position embedding to Transformers is an open problem. It can be understood as a kind of implicit coordinate basis of feature space, to provide temporal or spatial information to the Transformer. For cloud point [168] and sketch drawing stroke [167], their token element is already a coordinate, meaning that position embedding is optional, not necessary. Furthermore, position embedding can be regarded as a kind of general additional information. In other words, from a mathematical point of view, any additional information can be added, such as detail of the manner of position embedding, e.g., the pen state of sketch drawing stroke [167], cameras and viewpoints in surveillance [169]. There is a comprehensive survey [170] discussing the position information in Transformers. For both sentence structures (sequential) and general graph structures (sparse, arbitrary, and irregular), position embeddings help Transformers to learn or encode the underlying structures. Considered from the mathematical perspective of self-attention, i.e., scaled dot-product attention, attentions are invariant to the positions of words (in text) or nodes (in graphs), if position embedding information is missing.

• Self Attention (SA) operation = Scaled Dot-Product Attention

Given an input sequence, self-attention allows each element to attend to all the other elements, so that self-attention encodes the input as a fully-connected graph. Therefore, the encoder of Vanilla Transformer can be regarded as a fully-connected GNN encoder, and the Transformer family has the non-local ability of global perception, similar to the NonLocal Network [171].

• Masked Self-Attention (MSA)

In practice, modification of self-attention is needed to help the decoder of Transformer to learn contextual dependence, to prevent positions from attending to subsequent positions.

For instance, in GPT [91], an upper triangular mask to enable look-ahead attention where each token can only look at the past tokens. Masking can be used in both encoder [167], [172] and decoder of Transformer, and has flexible implementations, e.g., 0-1 hard mask [167], soft mask [172].

• Multi-Head Self-Attention (MHSA)

In practice, multiple self-attention sub-layers can be stacked in parallel and their concatenated outputs are fused by a projection matrix W, to form a structure named Multi-Head Self-Attention.

The idea of MHSA is a kind of ensemble. MHSA helps the model to jointly attend to information from multiple representation sub-spaces.

• Feed-Forward Network

The output of the multi-head attention sub-layer will go through the position-wise Feed-Forward Network (FFN) that consists of successive linear layers with non-linear activation.

1. Early Summation

In practice, early summation [45], [89] is a simple and effective multimodal interaction, where the token embeddings from multiple modalities can be weighted summed at each token position and then processed by Transformer layers. Its main advantage is that it does not increase computational complexity. However, its main disadvantage is due to the manually set weightings.

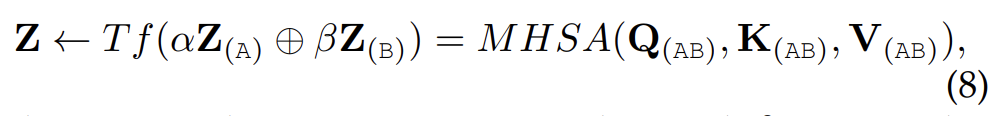
2. Early Concatenation = all-attention = CoTransformer

token embedding sequences from multiple modalities are concatenated and input into Transformer layers

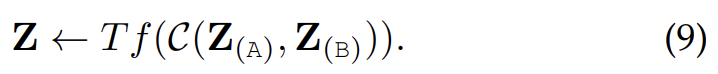
Thus, all the multimodal token positions can be attended as a whole sequence, such that the positions of each modality can be encoded well by conditioning the context of other modalities. However, the longer sequence after concatenation will increase computational complexity.

3. Hierarchical Attention (multi-stream to one-stream)

A common practice is that multimodal inputs are encoded by independent Transformer streams and their outputs are concatenated and fused by another Transformer. This kind of hierarchical attention is an implementation of late interaction/fusion, and can be treated as a special case of early concatenation.

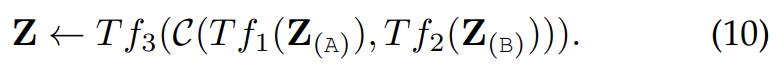
4. Hierarchical Attention (one-stream to multi-stream)

concatenated multimodal inputs are encoded by a shared single-stream Transformer that is followed by two separate Transformer streams. This method perceives the cross-modal interactions and meanwhile preserves the independence of uni-modal representation.

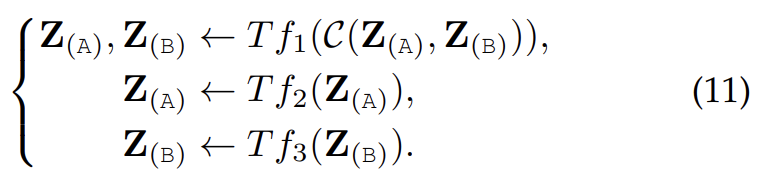
5. Cross-Attention = co-attention

For two-stream Transformers, if the Q (Query) embeddings are exchanged/swapped in a crossstream manner, the cross-modal interactions can also be perceived.

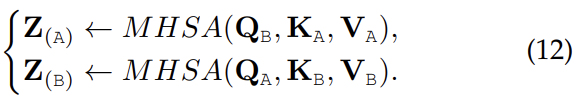
Cross-attention attends to each modality conditioned on the other and does not cause higher computational complexity, however if considered for each modality, this method fails to perform cross-modal attention globally and thus loses the whole context. As discussed in [190], two-stream crossattention can learn cross-modal interaction, whereas there is no self-attention to the self-context inside each modality.

6. Cross-Attention to Concatenation

The two streams of cross-attention [107] can be further concatenated and processed by another Transformer to model the global context. This kind of hierarchically cross-modal interaction is also widely studied [144], [192], and alleviates the drawback of cross-attention.

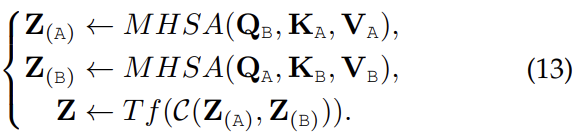
In general, if we consider from the angle of network structures, (1) early summation and early concatenation work in single-stream, (2) cross-attention work in multistreams, (3) hierarchical attention and cross-attention to concatenation work in hybrid-streams.

From the perspective of timing of interaction, these multimodal attentions fall into three categories, i.e., early interaction: early summation, early concatenation, and hierarchical attention (one-stream to multi-stream), late interaction: hierarchical attention (multi-stream to one-stream), or throughout interaction: cross-attention, cross-attention to concatenation.

• CLIP [123] is an inspiring solution that transfers knowledge across modalities by learning a shared multimodal embedding space, enabling zero-shot transfer of the model to down-stream tasks. The main inspiration that CLIP presents the community is that the pretrained multimodal (image and text) knowledge can be transferred to downstream zero-shot image prediction by using a prompt template “A photo of a {label}.” to bridge the distribution gap between training and test datasets.