정렬
정렬 시리즈 마지막은 병합 정렬과 기수 정렬이다. 기수 정렬은 많이 쓰이진 않지만 가장 짧은 시간 복잡도를 보이므로 방법은 알아두는 것이 좋다. 병합 정렬은 많이 쓰이는 방법으로 구현 코드까지 숙지를 해놓아야 한다.
04-5 병합 정렬
병합 정렬(merge sort)은 퀵 정렬과 마찬가지로 분할 정복 방식을 사용해 데이터를 분할하고 분할한 집합을 정렬하며 합치는 알고리즘이다. 병합 정렬의 시간 복잡도는 O(nlogn)이다.
병합 정렬의 핵심 이론
백문이 불여일견이다 그림으로 살펴보자.

그림을 보면 최초에는 8개의 그룹으로 나눈다. 이 상태에서 2개씩 그룹을 합치며 오름차순으로 정렬한다. 이어서 2개씩 그룹을 하치며 다시 오름차순을 정렬한다. 이런 방식으로 병합 정렬 과정을 거치면 (1, 2, 3, 4, 5, 6, 7)이 되어 전체를 오름차순으로 정렬할 수 있다.
2개의 그룹을 병합하는 과정
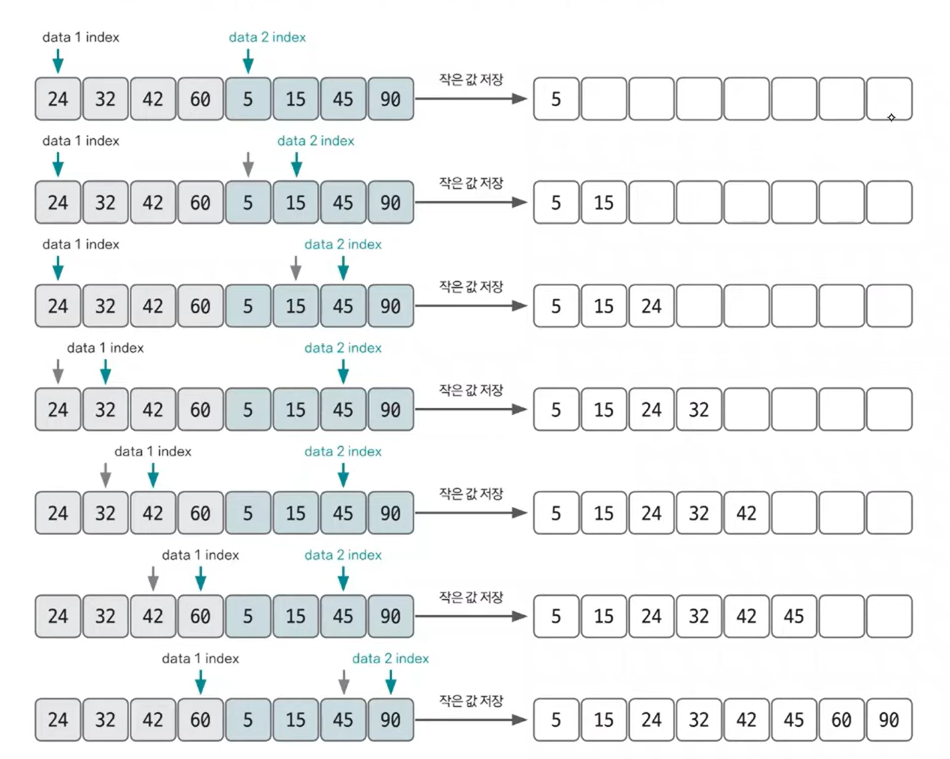
투 포인터 개념을 사용하여 왼쪽, 오른쪽 그룹을 병합한다. 왼쪽 포인터와 오른쪽 포인터의 값을 비교하여 작은 값을 결과 배열에 추가하고 포인터를 오른쪽으로 1칸 이동시킨다. 이 방식은 여러 문제에서 응용하므로 반드시 숙지해야 한다.
문제 020 수 정렬하기2
문제
N개의 수가 주어졌을 때, 이를 오름차순으로 정렬하는 프로그램을 작성하시오.
입력
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
출력
첫째 줄부터 N개의 줄에 오름차순으로 정렬한 결과를 한 줄에 하나씩 출력한다.
예제 입력 1
5
5
4
3
2
1
예제 출력 1
1
2
3
4
5
병합 정렬 코드이다. 병합 정렬을 실제로 쓰는 일은 많이 없어도 투 포인터를 쓰는 개념 활용하는 문제는 자주 출제됨으로 반드시 숙지해두자.
import sys
sys.stdin = open("input.txt", 'rt')
def Dsort(lt, rt):
if lt < rt:
mid = (lt+rt)//2
Dsort(lt, mid)
Dsort(mid+1, rt)
p1 = lt
p2 = mid+1
tmp = []
while p1 <= mid and p2 <= rt:
if a[p1] < a[p2]:
tmp.append(a[p1])
p1 += 1
else:
tmp.append(a[p2])
p2 += 1
if p1 <= mid:
tmp = tmp+a[p1:mid+1]
if p2 <= rt:
tmp = tmp+a[p2:rt+1]
for i in range(len(tmp)):
a[lt+i] = tmp[i]
if __name__ == "__main__":
n = int(input())
a = [0]*n
for i in range(n):
a[i] = int(input())
Dsort(0, n-1)
for x in a:
print(x)04-6 기수 정렬
기수 정렬(radix sort)은 값을 비교하지 않는 특이한 정렬이다. 기수 정렬은 값을 놓고 비교할 자릿수를 정한 다음 해당 자릿수만 비교한다. 기수 정렬의 시간 복잡도는 O(kn)으로, 여기서 k는 데이터의 자릿수를 말한다.
기수 정렬의 핵심 이론
기수 정렬은 10개의 큐를 이용한다. 각 큐는 값의 자릿수를 대표한다.
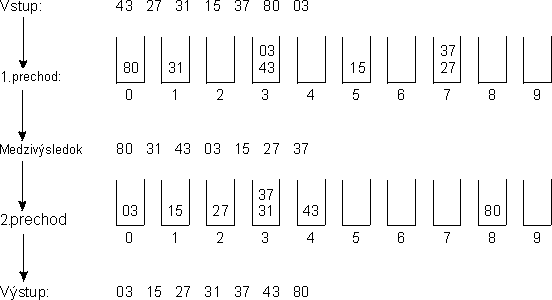
그림을 보면 원본 배열은 43, 27, 31, 15, 37, 80, 03이다. 그러면 일의 자릿수 기준으로 배열 원소를 큐에 집어 넣는다. 그런 다음 0번째 큐부터 9번째 큐까지 pop을 진행한다. 그 결과 80, 31, 43, 03, 15, 27, 37이 만들어진다. 이어서 십의 자릿수를 기준으로 같은 과정을 진행한다. 마지막 자릿수를 기준으로 정렬할 때까지 앞의 과정을 반복한다.
기수 정렬은 시간 복잡도가 가장 짧은 정렬로 만약 코테에서 정렬해야 하는 데이터의 개수가 너무 많으면 기수 정렬 알고리즘을 사용해보는 것이 좋다.
수 정렬하기 3
문제
N개의 수가 주어졌을 때, 이를 오름차순으로 정렬하는 프로그램을 작성하시오.
입력
첫째 줄에 수의 개수 N(1 ≤ N ≤ 10,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 10,000보다 작거나 같은 자연수이다.
출력
첫째 줄부터 N개의 줄에 오름차순으로 정렬한 결과를 한 줄에 하나씩 출력한다.
예제 입력 1
10
5
2
3
1
4
2
3
5
1
7
예제 출력 1
1
1
2
2
3
3
4
5
5
7
이 문제는 N의 최대 개수가 10,000,000으로 매우 크기 때문에 O(nlogn)보다 더 빠른 알고리즘이 필요하다. 문제에서 주어지는 숫자의 크기가 10,000보다 작다는 것을 바탕으로 기수 정렬과 함께 많이 사용하는 계수 정렬(counting sort)을 사용하여 문제를 해결하자. 계수 정렬은 로직이 기수 정렬보다 간단하다.
