정렬
오늘 정리할 것은 삽입 정렬과 퀵 정렬이다. 정렬하면 역시 퀵 정렬과 병합 정렬이라 할 수 있는데 오늘은 그 유명한 퀵 정렬이 무엇인지 알아보자.
04-3 삽입 정렬
삽입 정렬은 이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입시켜 정렬하는 방식이다. 시간 복잡도는 O(n^2)으로 느린 편이지만 구현하기가 쉽다.거짓말...
삽입 정렬의 핵심 이론
선택 데이터를 현재 정렬된 데이터 범위 내에서 적절한 위치에 삽입하는 것이 삽입 정렬의 핵심이다. 핵심 이론을 좀 더 풀어서 쓰자면 선택한 데이터을 집고 앞 칸들을 돌다가 자기가 들어갈 자리를 찾으면 다 밀어버리고 그 자리에 쏙 넣으면 되는 것이다. 다른 데이터를 밀어내는 게 꼭 슬라이딩 퍼즐이랑 비슷하다. (백문이 불여일견)
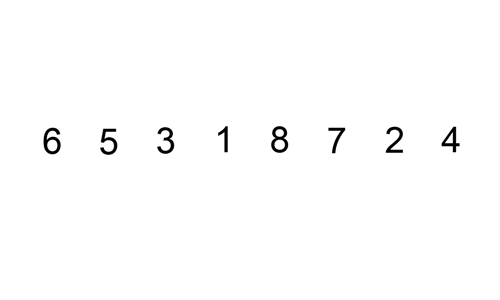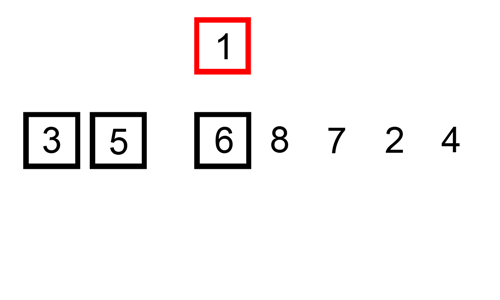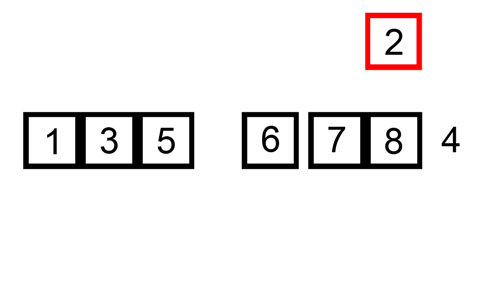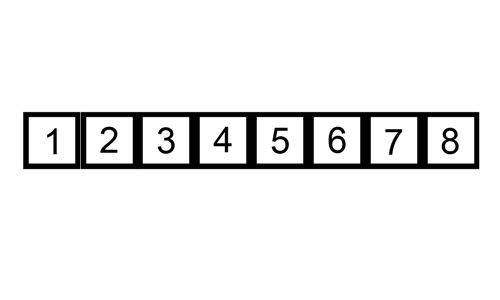
삽입 정렬 수행 방식
삽입 정렬의 자세한 과정은 다음과 같다.
-
현재 index에 있는 데이터 값을 선택한다.
-
현대 선택한 데이터가 정렬된 데이터 범위에 삽입될 위치를 탐색한다.
-
삽입 위치부터 index에 있는 위치까지 shift 연산을 수행한다.
-
삽입 위치에 현재 선택한 데이터를 삽입하고 index++ 연산을 수행한다.
-
전체 데이터의 크기만큼 index가 커질 때까지, 즉 선택할 데이터가 없을 때까지 반복한다.
적절한 삽입 위치를 탐색하는 부분에서 이진 탐색 등과 같은 탐색 알고리즘을 사용하면 시간 복잡도를 줄일 수 있다. 하지만 결국 밀어내는 shift 연산을 수행해야 하기 때문에 여전히 효율적인 정렬 알고리즘이라고 보기는 어렵다.
문제 018 ATM 인출 시간 계산하기
인하은행에는 ATM이 1대밖에 없다. 지금 이 ATM앞에 N명의 사람들이 줄을 서있다. 사람은 1번부터 N번까지 번호가 매겨져 있으며, i번 사람이 돈을 인출하는데 걸리는 시간은 Pi분이다.
사람들이 줄을 서는 순서에 따라서, 돈을 인출하는데 필요한 시간의 합이 달라지게 된다. 예를 들어, 총 5명이 있고, P1 = 3, P2 = 1, P3 = 4, P4 = 3, P5 = 2 인 경우를 생각해보자. [1, 2, 3, 4, 5] 순서로 줄을 선다면, 1번 사람은 3분만에 돈을 뽑을 수 있다. 2번 사람은 1번 사람이 돈을 뽑을 때 까지 기다려야 하기 때문에, 3+1 = 4분이 걸리게 된다. 3번 사람은 1번, 2번 사람이 돈을 뽑을 때까지 기다려야 하기 때문에, 총 3+1+4 = 8분이 필요하게 된다. 4번 사람은 3+1+4+3 = 11분, 5번 사람은 3+1+4+3+2 = 13분이 걸리게 된다. 이 경우에 각 사람이 돈을 인출하는데 필요한 시간의 합은 3+4+8+11+13 = 39분이 된다.
줄을 [2, 5, 1, 4, 3] 순서로 줄을 서면, 2번 사람은 1분만에, 5번 사람은 1+2 = 3분, 1번 사람은 1+2+3 = 6분, 4번 사람은 1+2+3+3 = 9분, 3번 사람은 1+2+3+3+4 = 13분이 걸리게 된다. 각 사람이 돈을 인출하는데 필요한 시간의 합은 1+3+6+9+13 = 32분이다. 이 방법보다 더 필요한 시간의 합을 최소로 만들 수는 없다.
줄을 서 있는 사람의 수 N과 각 사람이 돈을 인출하는데 걸리는 시간 Pi가 주어졌을 때, 각 사람이 돈을 인출하는데 필요한 시간의 합의 최솟값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 사람의 수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 각 사람이 돈을 인출하는데 걸리는 시간 Pi가 주어진다. (1 ≤ Pi ≤ 1,000)
출력
첫째 줄에 각 사람이 돈을 인출하는데 필요한 시간의 합의 최솟값을 출력한다.
예제 입력 1
5
3 1 4 3 2
예제 출력 1
32
정렬 알고리즘 자체는 그리 어렵진 않지만 구현할 때 범위를 잘 지정해야 하므로 은근히 헷갈린다. 주의해야할 점은 리스트를 뒤에서 거꾸로 돌 때, 즉 step이 -1일 땐 end가 -1이어야지 인덱스 0까지 돈다. 예를 들어 10번 부터 0번까지 돌고 싶다면 range(10, -1, -1)로 적어야 한다.
n = int(input())
a = list(map(int, input().split()))
s = [0] * n
for i in range(1, n):
insert_point = i
insert_value = a[i]
for j in range(i-1, -1, -1): # step이 -1인 경우 end+1 까지 돈다...!
if a[j] < a[i]:
insert_point = j+1
break
if j == 0:
insert_point = 0
for j in range(i, insert_point, -1):
a[j] = a[j-1]
a[insert_point] = insert_value
s[0] = a[0]
for i in range(1, n):
s[i] += s[i-1] + a[i]
sum = 0
for i in range(0, n):
sum += s[i]
print(sum)04-4 퀵 정렬
퀵 정렬은 기준값을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬하는 알고리즘이다. 기준값이 어떻게 선정되는지가 시간 복잡도에 많은 영향을 미치고, 평균적인 시간 복잡도는 O(nlogn)이며 최악의 경우에는 시간 복잡도가 O(n^2)이다.
퀵 정렬의 핵심 이론
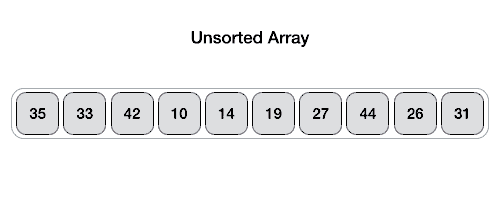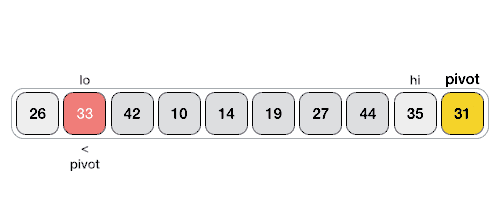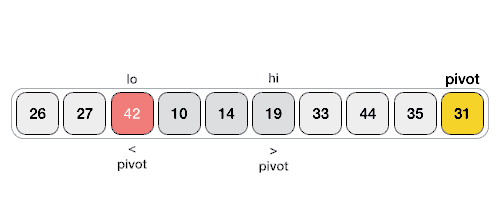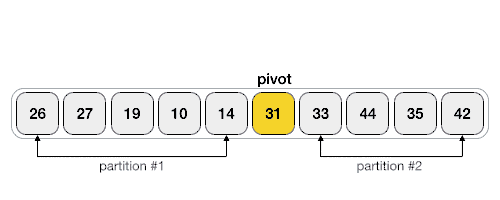
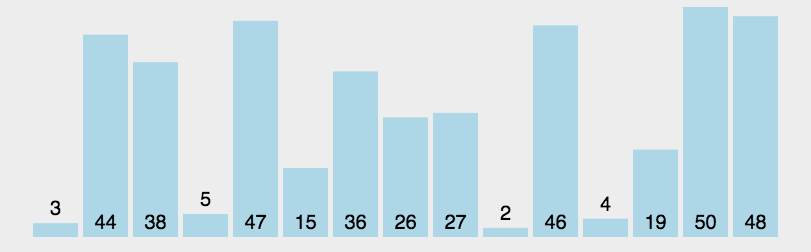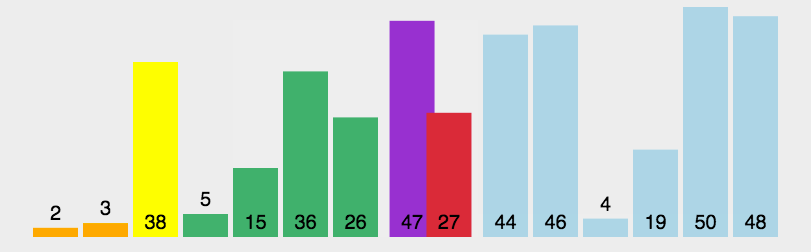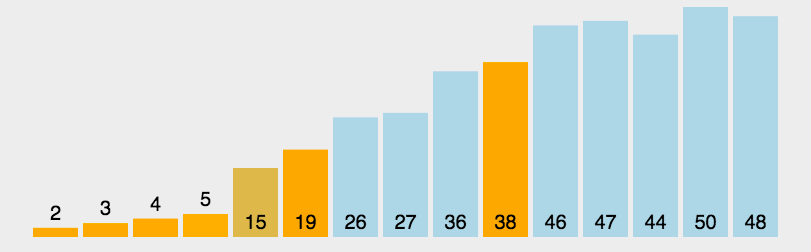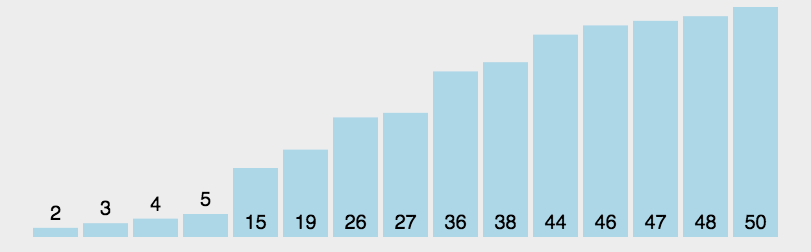
pivot을 중심으로 계속 데이터를 2개의 집합으로 나누면서 정렬하는 것이 퀵 정렬의 핵심이다. 우선 그림으로 확인해보자.
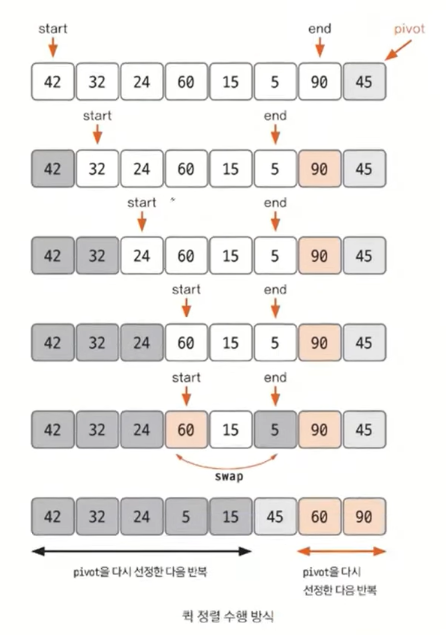
퀵 정렬의 특징은 하나의 pivot을 기준으로 왼쪽에는 작은 값을, 오른쪽은 큰 값을 배치한다. 이 과정을 모든 부분 집합에 대해 수행하게 되면 정렬이 완료되는 것이다. 주목할 점은 작은 값과 큰 값을 두 부분으로 나누기 때문에 pivot이 놓이는 자리는 정렬이 완료된 이후에도 변하지 않는다.
퀵 정렬 과정
-
데이터를 분할하는 pivot을 설정한다(위 그림의 경우 가장 오른쪽 끝을 pivot으로 설정).
-
pivot을 기준으로 다음 a~e 과정을 거쳐 데이터를 2개의 집합으로 분리한다.
2-a. start가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start를 오른쪽으로 1칸 이동한다.
2-b. end가 가리키는 데이터가 pivot이 가리키는 데이터보다 크면 end를 왼쪽으로 1칸 이동한다.
2-c. start가 가리키는 데이터가 pivot이 가리키는 데이터보다 크고, end가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start, end가 가리키는 데이터를 swap하고 start는 오른쪽, end는 왼쪽으로 1칸씩 이동한다.
2-d. start와 end가 만날 때까지 2.a ~ 2.c를 반복한다.
2-e. start와 end가 만나면 만난 지점에서 가리키는 데이터와 pivot이 가리키는 데이터를 비교하여 pivot이 가리키는 데이터가 크면 만난 지점의 오른쪽에, 작으면 만난 지점의 왼쪽에 pivot이 가리키는 데이터를 삽입한다. -
분리 집합에서 각각 다시 pivot을 선정한다.
-
분리 집합이 1개 이하가 될 때까지 과정 1~3을 반복한다.
퀵 정렬은 중요하니 두 개 정도 넣어준다. 퀵 정렬은 하는 방법은 양쪽 끝을 탐색하며 partion하는 방법도 있지만 좀 더 구현하기 쉬운 방법으로 i와 pos를 이용하는 방법도 있다. 19번 문제를 통해 ipos(내가 지은 이름이다)방법을 알아보자.
문제 019 K번째 수 구하기
문제
수 N개 A1, A2, ..., AN이 주어진다. A를 오름차순 정렬했을 때, 앞에서부터 K번째 있는 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N(1 ≤ N ≤ 5,000,000)과 K (1 ≤ K ≤ N)이 주어진다.
둘째에는 A1, A2, ..., AN이 주어진다. (-10^9 ≤ Ai ≤ 10^9)
출력
A를 정렬했을 때, 앞에서부터 K번째 있는 수를 출력한다.
예제 입력 1
5 2
4 1 2 3 5
예제 출력 1
2
N의 개수가 5,000,000개이므로 시간복잡도는 최소 O(nlogn)이 되어야 한다. 이 문제에선 퀵 정렬을 사용하는 것이 효과적인데 sort()를 사용하고 K번째 수를 출력하는 것도 가능하겠지만 보다 빠른 방법으로 퀵 정렬의 특성을 이용하는 것이 있다. 퀵 정렬은 하나의 값의 위치를 한 번 정하면 변하지 않는다는 특성이 있다. 즉, 정렬된 배열에서 그 값의 위치를 알 수 있기 때문에 K번째 자리의 숫자만을 구하는 문제에선 다 정렬하지 않아도 그 값을 구할 수 있다. 다음 코드를 보자.
import sys
sys.stdin = open('input.txt', 'rt')
def Qsort(lt, rt):
if lt < rt:
pos = lt
pivot = arr[rt]
for i in range(lt, rt):
if arr[i] <= pivot:
arr[i], arr[pos] = arr[pos], arr[i]
pos += 1
arr[rt], arr[pos] = arr[pos], arr[rt]
if pos == k-1:
print(k)
sys.exit(0)
Qsort(lt, pos-1)
Qsort(pos+1, rt)
if __name__ == "__main__":
n, k = map(int, input().split())
arr = list(map(int, input().split()))
Qsort(0, n-1)
위의 코드는 ipos 퀵 정렬을 썼다. 같은 퀵 정렬이지만 구현하기 조금 더 쉽다는 장점이 있다.
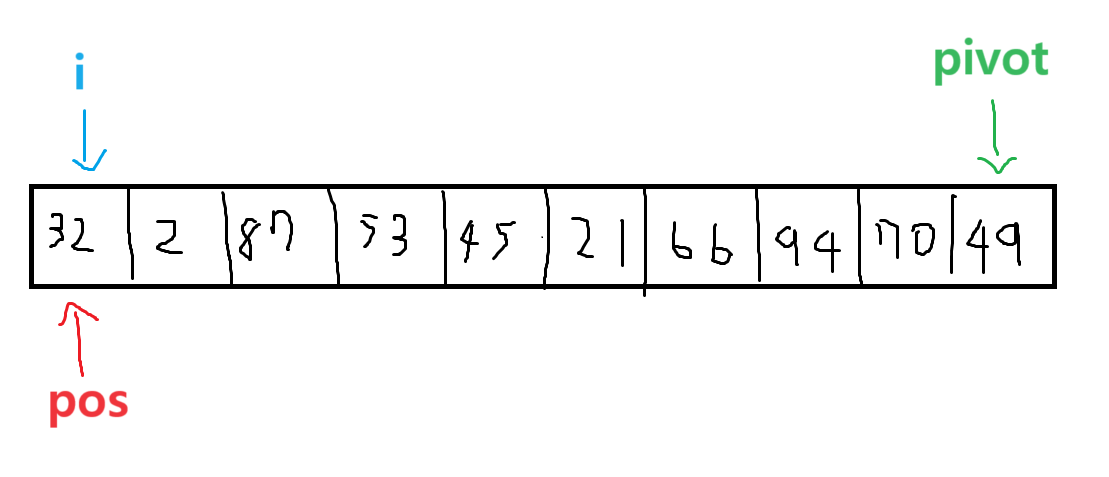
ipos 퀵 정렬에서 i는 배열을 쭉 돌면서 pivot 값과 비교하는 역할을 하고, pos는 pivot 자리를 정하는 역할과 pivot보다 작은 arr[i] 값이 있다면 arr[pos]값과 swap 해주는 역할을 한다. 이 방법은 구현이 쉽긴 하지만 정석은 위의 방법이므로 위에서 설명한 퀵 정렬의 원리는 반드시 숙지하고 있어야 한다.

띠용???
첫번째 풀이 방법은 Do it의 알고리즘, 두번째는 ipos 구현, 세번째는 갓갓 sort()를 이용한 방법이다. 어째선지 위의 코드대로 짜면 시간 초과가 난다. 이제부터 그 이유를 알아보고자 한다. 같은 퀵 정렬인데 넌 왜...?
퀵 정렬은 기본적으로 O(nlogn)의 시간복잡도를 가진다. 하지만 최악의 상황에선 O(n2)의 시간복잡도를 가진다. 그렇다면 어떤 경우를 최악의 경우라고 할 수 있을까?
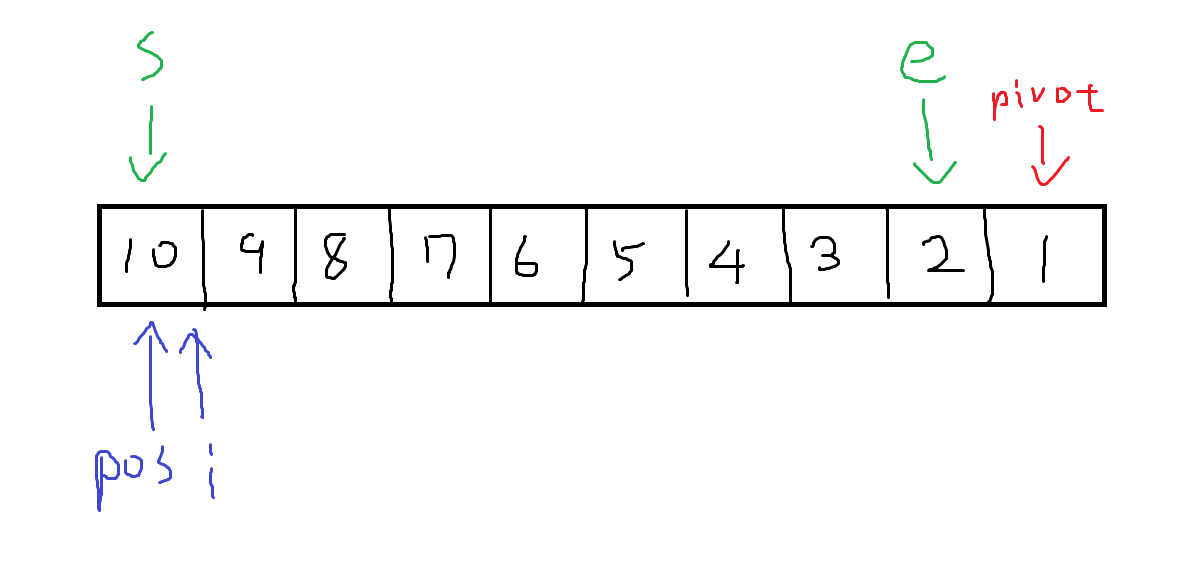
내림차순으로 정렬된 배열을 오름차순으로 바꾸는 상황은 생각보다 흔하다. 이럴 때 처음에 배웠던 정석적인 퀵정렬 방법(초록색)은 앞쪽과 뒷쪽에서 다시말해 양방향에서 돌기 때문에 O(nlogn)의 시간 복잡도를 가진다. 하지만 ipos 방법은 0부터 돌기 때문에 이 경우 최악의 시간 복잡도인 O(n2)을 가진다. 이 때문에 모든 케이스를 테스트하는 백준에선 시간 초과가 뜬다. 실험해보니 pivot 값을 중간값으로 설정해도 마찬가지로 시간초과가 뜬다. 따라서 코딩테스트에선 단방향을 쓰는 것을 지양하고 양방향을 써야 한다. 다음은 정석적인 퀵 정렬 코드이다.
n, k = map(int, input().split())
a = list(map(int, input().split()))
def quickSort(s, e, k):
global a
if s < e:
pivot = partition(s, e)
if pivot == k:
return
elif k < pivot:
quickSort(s, pivot-1, k)
else:
quickSort(pivot+1, e, k)
def swap(i, j):
global a
tmp = a[i]
a[i] = a[j]
a[j] = tmp
def partition(s, e):
global a
if s + 1 == e:
if a[s] > a[e]:
swap(s, e)
return e
m = (s+e) // 2
swap(s, m)
pivot = a[s]
i = s+1
j = e
while i <= j:
while pivot < a[j] and j > 0:
j = j-1
while pivot > a[i] and i < len(a)-1:
i = i+1
if i <= j:
swap(i, j)
i = i+1
j = j-1
a[s] = a[j]
a[j] = pivot
return j
quickSort(0, n-1, k-1)
print(a[k-1])조금 복잡할 수 있지만 이 방법을 잘 숙지해야 한다. 사실 함수를 많이 선언했을 뿐이지 그리 복잡한 코드는 아니니 자세히 잊혀질 때마다 다시 보자. 다만 이 코드는 K번째 수를 찾는 데 적합한 코드라서 배열을 정렬할땐 변형시켜야 할 것이다.
퀵 정렬의 핵심 논리
사실 퀵 정렬에서 가장 이해 안되는 부분이 있었다. pivot을 정하고 s와 e가 돌게 된다. s는 pivot보다 작을 경우 s++가 되고, e는 pivot보다 큰 경우 e--가 연산된다. s와 e가 멈췄을 때 s <= e라면 두 index가 가리키는 데이터는 swap된다. 그리고 s와 e가 서로 엇갈릴 때 pivot과 swap되며 끝난다.
내가 가장 이해 안되는 부분이 여기다. pivot은 어떤 값과 swap되어야 하는가? s와 e가 만난 index와 바뀌어야 하나? 근데 그렇게 되면 반드시 pivot 값이 정렬된다는 보장이 없다. 퀵 정렬은 반드시 자리를 확정하는 특성이 있는데 말이다. 만난 부분(m)의 값보다 pivot이 작으면 m-1에 크면 m+1d에 저장하는 방법은? 그렇게 되면 pivot의 자리는 확정되지만 다른 값을 다 밀어야 하므로 비효율적인 연산이 된다.
arr = [63, 15, 10, 27, 77, 58, 46, 34, 81]
def Qsort(arr, s, e):
if s > e:
return
pivot = s
lt = s + 1
rt = e
while lt <= rt:
while(lt <= e) and arr[lt] <= arr[pivot]: #lt 이동
lt += 1
while rt > s and arr[rt] >= arr[pivot]: #rt 이동
rt -= 1
if lt > rt:
arr[rt], arr[pivot] = arr[pivot], arr[rt] #pivot swap
else:
arr[lt], arr[rt] = arr[rt], arr[lt] #lt, rt swap
#재귀함수로 부분 정렬
Qsort(arr, s, rt-1)
Qsort(arr, rt+1, e)
Qsort(arr, 0, len(arr)-1)
print(arr)가장 깔끔하다고 생각하는 퀵 정렬 코드이다. 이 부분에서 주목할 점은 pivot을 swap하는 부분이다. 코드를 보면 고정적으로 rt와 pivot값을 바꿔주고 있다. 왜 하필 rt일까? lt가 될 수는 없는 걸까. 여기서 걸리는 바람에 많은 시간을 소모했다. 위 코드를 보면 pivot을 s에 저장한다. 따라서 오름차순으로 정렬한다면 pivot은 항상 가장 작은 숫자가 존재하는 위치이다. pivot이 swap될 조건은 lt, rt가 엇갈리는 경우이다. 다시 말해 rt가 lt 왼쪽으로 오면서 항상 작은 값을 갖게 된다는 말이다. 퀵 정렬은 pivot 값을 기준으로 왼편에는 작은 값을, 오른편엔 큰 값을 나누는 작업을 반복한다. pivot이 왼쪽 끝에 있었기 때문에 바꿨을 때 작은 값이 왼편에 오도록 항상 rt와 바꿔주게 되는 것이다. 만약 pivot을 오른쪽에서 가져왔다면 rt가 아닌 큰 값을 담고 있는 lt와 바꿔주었을 것이다.
이 부분이 이해가 안되는 바람에 꽤나 고생을 한 것 같다... 끝!
