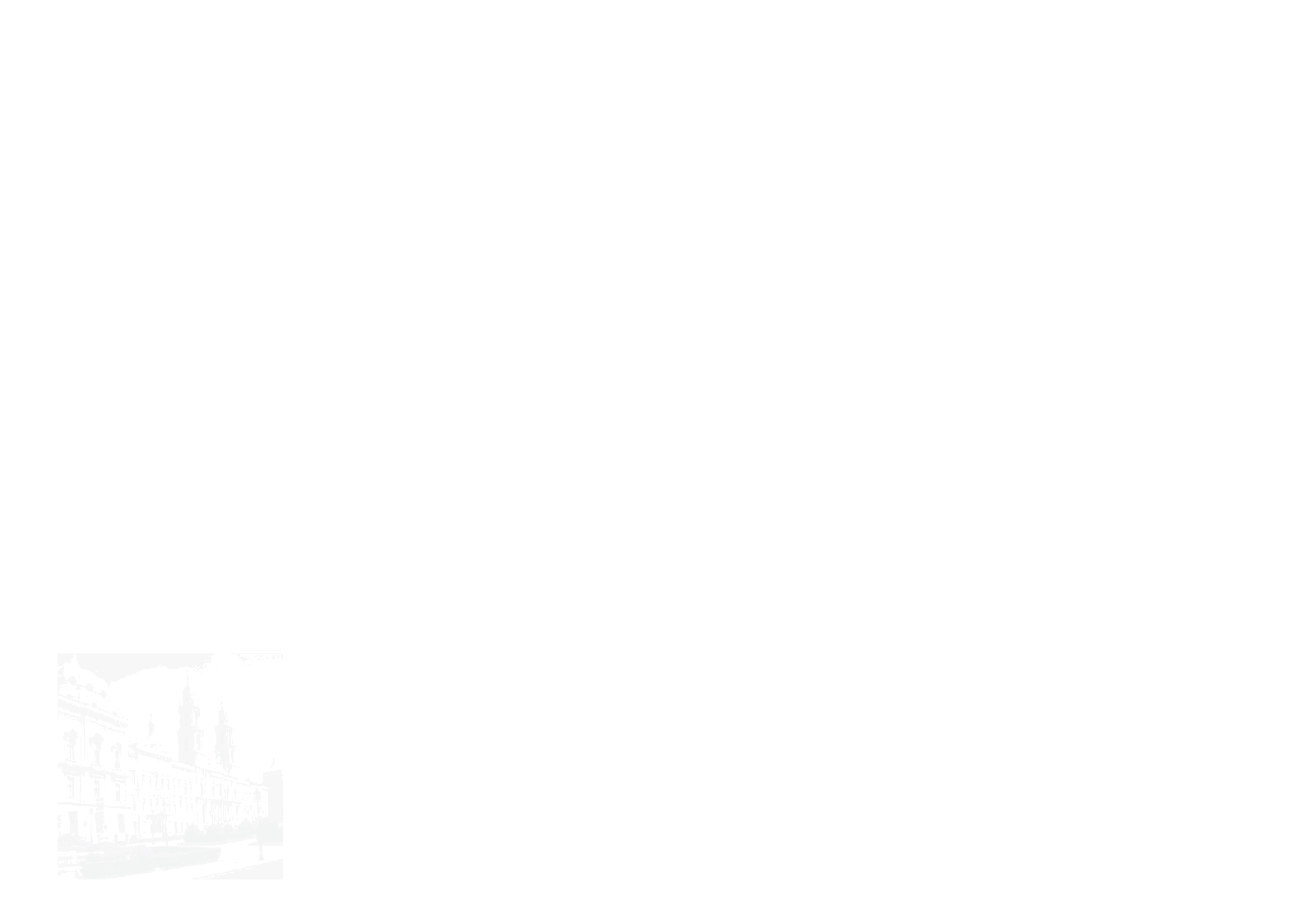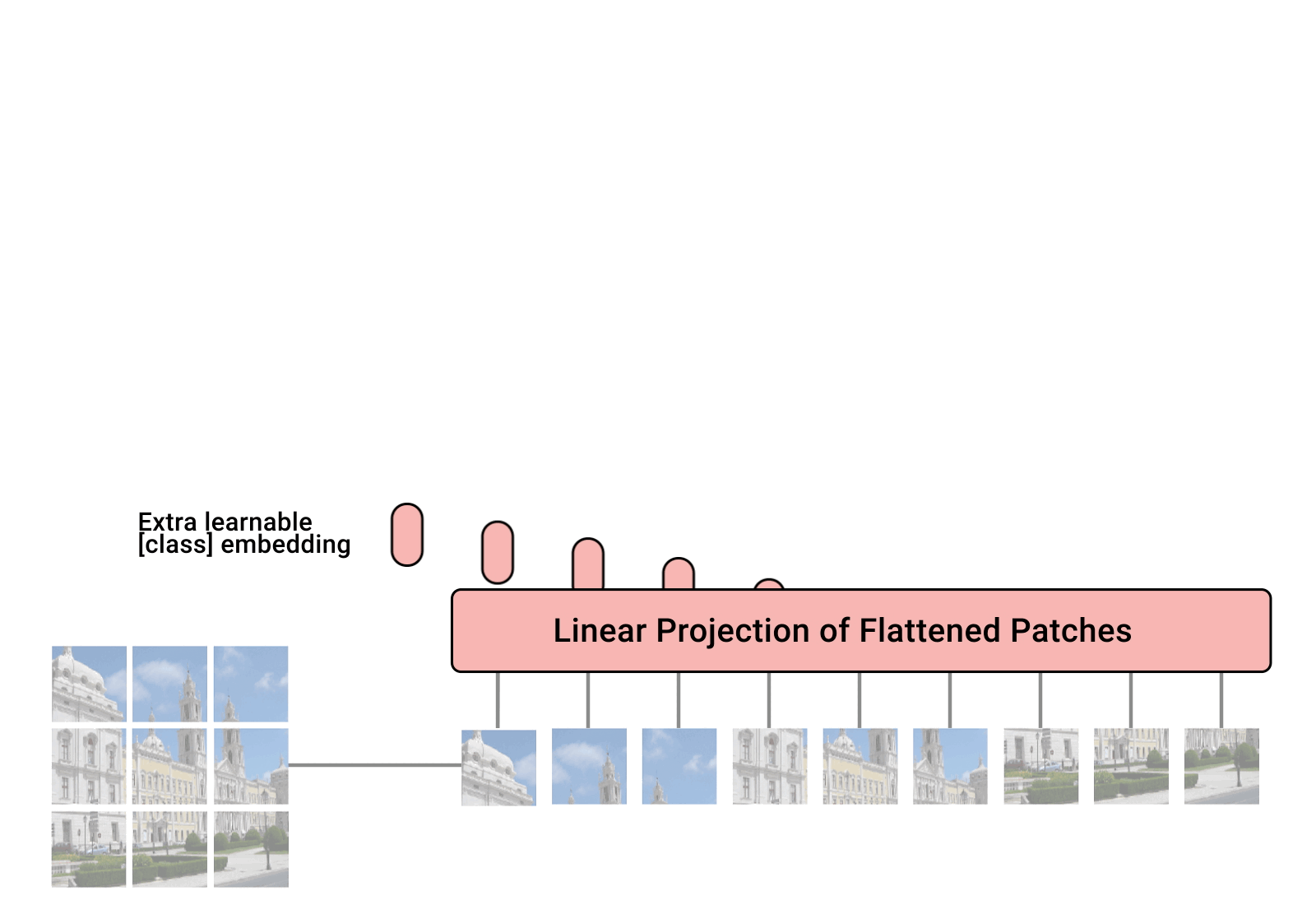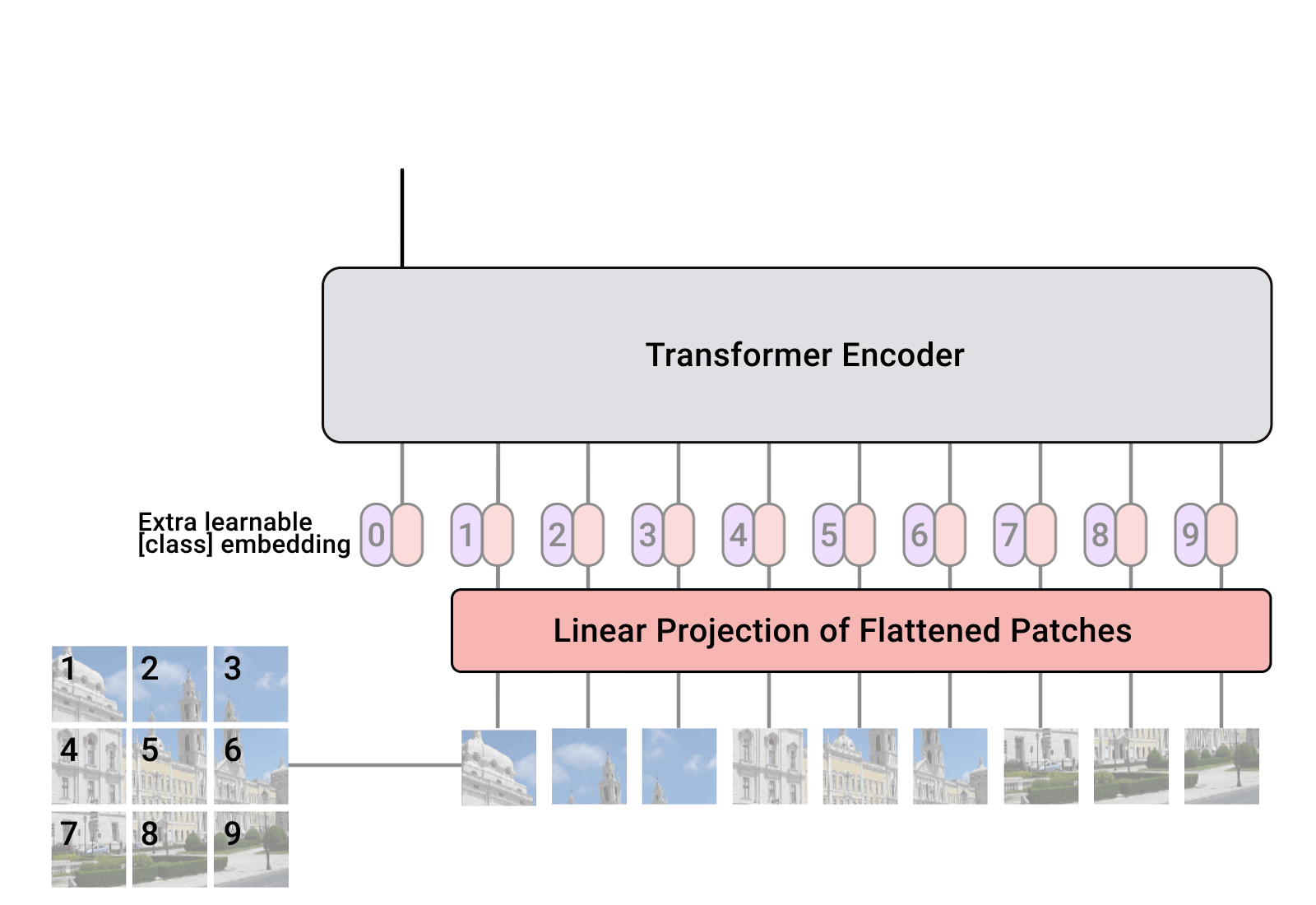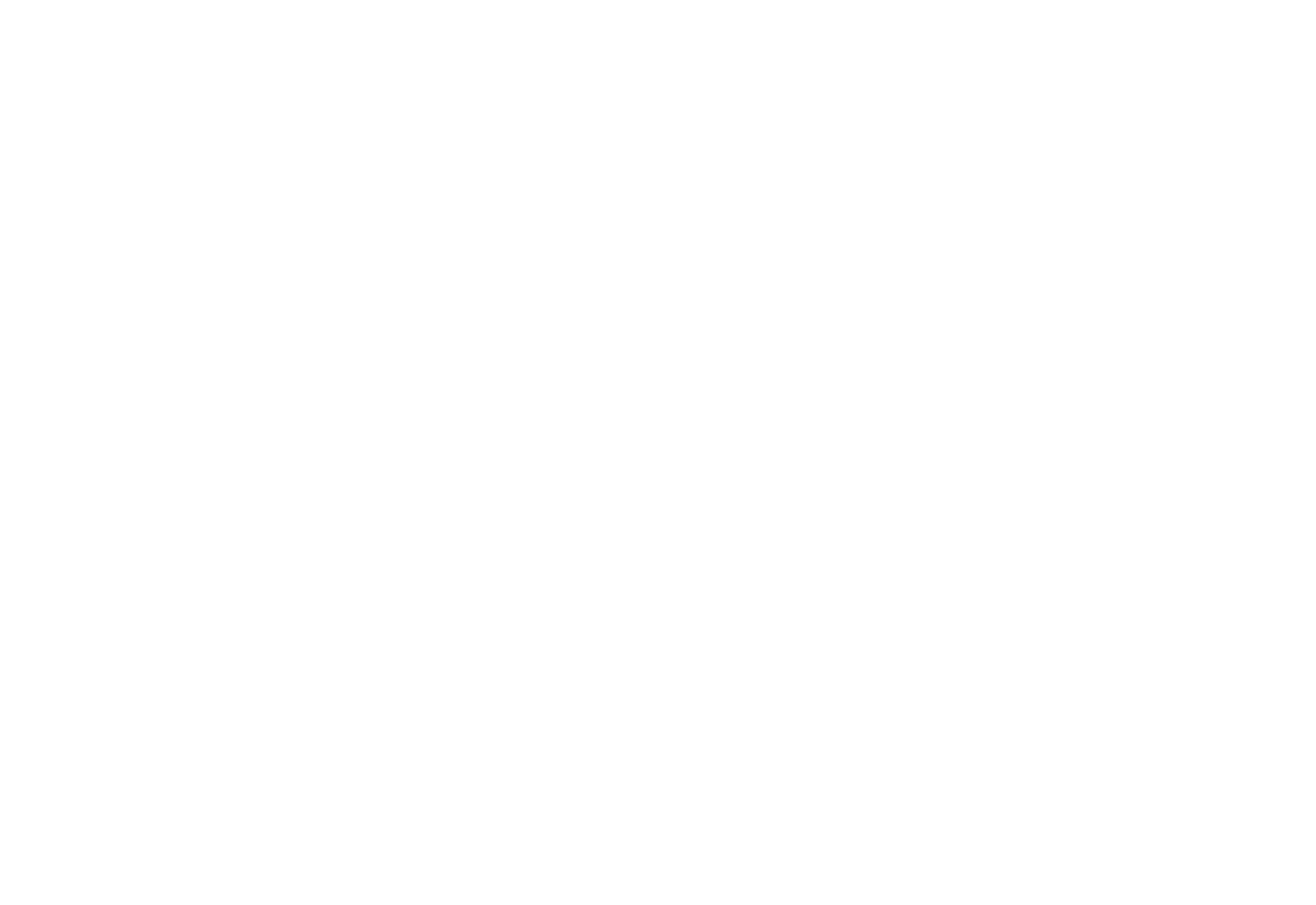[논문리뷰] ViT: OpenAI sora DiTs 의 근간

논문 : AN IMAGE IS WORTH 16X16 WORDS : TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE

참고하면 이해하기 좋음 : https://github.com/lucidrains/vit-pytorch

다른 블로그를 덜 참조할 수 있도록, All in one 느낌으로 정리하다보니 글이 너무 길어졌다. 그래서 글의 구조를 두괄식 구조 로 바꾸었다. "실험에 대한 해석" 부분은 처음엔 대충 읽고, "ViT 구조" 까지 읽어보신 후에 다시 한번 읽어보시는 것을 추천한다.

Related :

Batch vs Layer Normalization

[Transformer] QKV ( query, key, value ) ?

[Transformer] Multi-Head Self-Attention ( MSA )

INDUCTIVE BIAS

위의 [Transformer] Multi-Head Self-Attention ( MSA ) 를 제외하고는 금방 읽고 오니 참고하라. 이 논문리뷰를 이해하는데에 많은 도움이 될 것이다.

목차

• 서론
• ViT: 이미지 인식의 새 지평을 열다(abstract)
• 결론
• 실험에 대한 해석
• ViT 구조
  1. 패치 분할
  2. Flattened Patches
  3. Patch + Position Embedding
  4. Transformer Encoder
  5. MLP Head
• Dits: ViT 그 이후 연구
• 본문 이해를 위한 참고 : Self-Attention for MSA

---

서론

OpenAI 의 Sora 에 대한 반응이 굉장히 뜨겁다. 아직 정식 출시된 것은 아니지만, 공개된 영상으로 봤을 때 믿기지 않을정도로 정교한 동영상 퀄리티를 보여주고있기 때문이다. 이번 포스팅은 OpenAI 의 Sora 가 사용하는 DiTs(Diffusion Transformers) 의 거의 근간 모델이라고 할 수 있는 ViT(Vision Transformer) 에 대해 알아보려고한다. ViT는 Computer Vision 분야에 Transformer 를 최초로 도입한 모델이다.

ViT: 이미지 인식의 새 지평을 열다

기존의 CNN(Convolutional Neural Network)은 이미지 인식과 분류 작업에서 전통적으로 사용된 방식이다. 하지만, CNN은 차원을 축소시키는 과정에서 정보의 손실이 발생한다. 또한, Convolution 연산을 사용하기에 지역적인 정보( locality )에 초점을 맞추며, 전역적인 문맥을 파악하는 데 한계가 있다. ViT 가 하고자 하는 것은 결국엔 CNN의 목적과도 같은 Image Classification 이다. input 으로 이미지가 들어왔을 때, 이 이미지가 무슨 이미지인지 구별하는 것이다.

NLP 분야에서 Transformer가 큰 성공을 거두면서 Computer Vision 분야에도 많은 영향이 미쳤다. ViT 전까지의 연구들은 Transformer의 핵심인 Self Attention 을 CNN에 적용하는 연구가 주를 이루었다면, ViT 이 후로는 Transformer 구조 자체를 Computer Vision 분야에 적용한 연구들이 활발하게 진행되고있다. 이번 글에서 Transformer를 이미지 분류 문제에 적용한 Vision Transformer(ViT)에 대해 소개하겠다.

목차로 돌아가기

---

결론

CNN 모델은 convolution layer 가 locality 한 특성을 잘 캐치해내지만 ViT 자체적으로는 locality 한 특성보다는 global 한 특성을 갖고있다. 즉, 이미지 전체를 학습하기에 패치들간 spatial relation 에 대한 학습이 필요하다. 따라서 ViT는 inductive bias가 없다고 할 수 있다. 그에 따라 더 많은 데이터를 통해 학습시켜야 일반화 성능을 갖출 수 있다.

더 많은 데이터를 통해 학습해야 한다고 했지만, 사실 JFT 라는 100M, 300M 이 넘는 학습 가능한 이미지 데이터를 갖추기란, 일반 기업 및 사용자 입장에서는 거의 불가능에 가깝다. 어찌보면 "우리가 만든 이미지 분류기가 있는데 너네가 학습할 필요 없고(할 수도 없고) 그냥 써" 에 가깝다.

그리고 현재 2024 년 3월 13일 기준으로 Transformer 는 fancy 하게 구성한 것보다 ( ex. 본문에서 얘기한 hybrid 와 같은 ) Transformer 순정 모델이 더 많이 사용된다고 한다. 그리고 사실 ViT 의 성능이 좋은 이유는 'Self-Attention 연산 때문인가?' 에 대한 실험으로 진행한 MLP-Mixer 라는 논문이 있다. 이 논문에서 사용한 아키텍처는 Transformer 없이 DNN의 MLP 만으로 이루어진다. 반전으로, MLP-Mixer 와 ViT 모델의 성능은 트레이닝 사이즈에 따라 다르긴한데, JFT 10M 에서는 ViT 의 accuracy 가 더 좋고, JFT 100M 부터는 거의 차이가 없는 것으로 나왔다( Compute 리소스는 ViT 보다 더 적게 요구된다 ).

논문 : MLP-Mixer: An all-MLP Architecture for Vision
이 논문은 이 ViT 글에 대해서 어느정도 이해했다면 쉽게 접근할 수 있는 논문이다. 궁금하다면 재미삼아 읽어봐도 좋을 것 같다. 많이 심플해서 깜짝놀랄 것이다.

목차로 돌아가기

---

실험에 대한 해석

포지션 임베딩

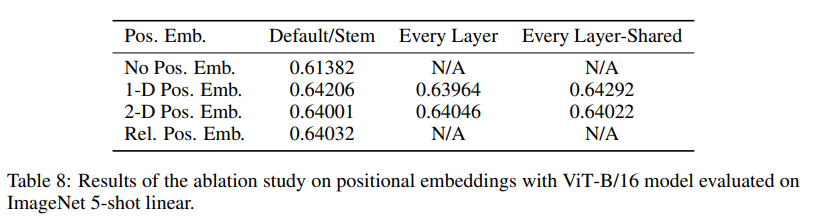
사실 이 논문에서 기준으로 잡은 Position Embedding 방식은 1-D Pos. Emb. 으로 raster scan 패턴을 사용해서 각 패치들을 Flatten 한 후 Linear Projection 했다. raster scan 패턴이란 별거 없다 그냥 아래 이미지를 보면 한방에 이해된다.

• No Pos. Emb 은 위치 정보를 제공하지 않고 bag 에 넣고 랜덤으로 뽑는 방식을 말한다.
• 2-D Pos. Emb. 은 행렬처럼 이미지를 x,y 축이 존재하는 2D 좌표로 보겠다는 말이다. (1,1), (1,2), ... (16, 16) 와 같이 이미지 좌표를 말한다.
• Rel. Pos. Emb. 은 패치간의 거리를 상대적 공간 정보로 인코딩한다.
• 결과는 1-D Pos. Emb. 을 채택했었을 때의 Position Embedding 의 코사인 유사도가 가장 1에 가까웠다( 유사도가 높다는 말 ).

데이터셋 훈련과 정확도

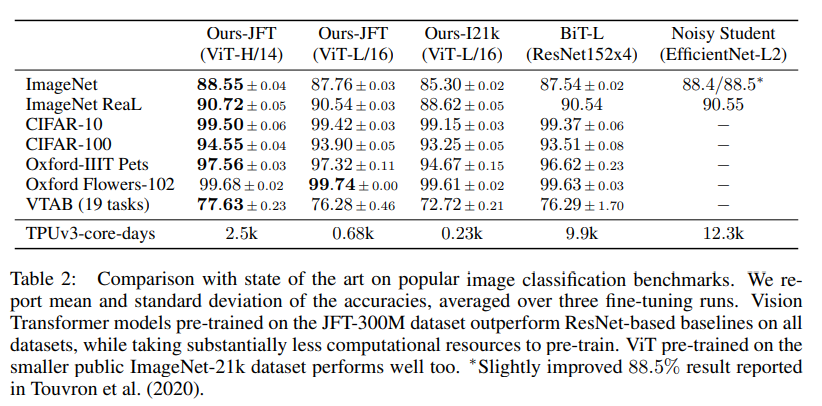
위의 테이블에서 가장 첫번째 열 즉 Ours-JFT(ViT-H/14) 부분이 다른 모델보다 정확도가 대부분 가장 좋은 지표를 보이고 있다. 하지만 여기서 조금 간과할 수도 있는 부분은 14로 나눈 패치는 연산량이 높아지기 마련이다. 그렇기에 사실상 ViT-L/16 을 효율적인 지표로 생각하는게 좋을 것이다.

첫번째 열 기준으로 위 테이블을 읽는 방법은 "ViT-H/14 모델로 JFT-300M 을 pretraining 시킨 후, ImageNet 벤치마크에서 88.55% 의 정확도를 달성했다" 로 보면 된다.

데이터 셋 훈련량과 성능

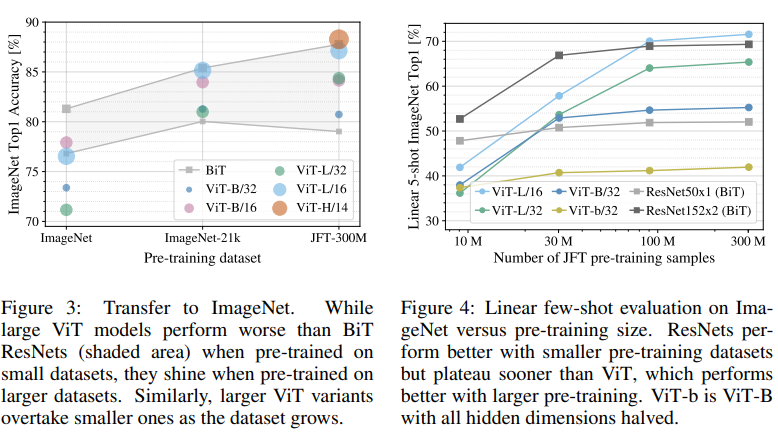
Figure 3을 통해 데이터 셋의 훈련량이 많아짐에 따른 ViT 의 정확도 향상을 볼 수 있다. 숫자 뒤에 M은 Million(백만) 단위를 말하는데, 다시말하면 저 정도의 훈련 데이터 셋이 있어야 ViT 가 BiT (ResNet) 보다 성능이 좋아진다 라고 보면 된다.

Figure 3에서의 y축은 정확도였지만 Figure 4에서의 y축은 Linear 5-shot 이다. 이 지표에 대해 이해하려면 few-shot learning 에 대해서 조금은 알고 있는 게 좋지만 여기서는 넘어가도록 하겠다. "학습과 추론도를 평가 하는 지표" 정도로 생각하는게 좋을 것 같다. 여기서 말하는 5-shot ImageNet 이란 ImageNet 에서 30, 40, 50, 60, 70 개 클래스(ex: 강아지, 고양이, 새, 자동차 등 등) 를 임의로 선정하고, 그 임의로 선정된 클래스 내에 이미지 5개만 두겠다는 말이다. 예를들자면, 강아지 사진 5개, 고양이 사진 5개, 새 사진 5개, 등 등..

그리고 왜 내가 위에서 "학습과 추론도를 평가 하는 지표" 라고 말했냐면, 학습된 것이 있으면 당연히 맞출 것이고, 학습되지 않은 이미지가 등장해도 "이 것은 아마도 이 것일 것이다." 를 추론해야 하기 때문이다. 예를들어, 강아지와 여우라는 분류 공간이 있다고 생각하자. 하지만 나는 강아지만 봐왔고 여우는 본 적이 없다. 그렇기에 여우 사진을 본다면 나는 여우를 보거나 배운 적은 없어도, 강아지를 알기에 "이 것은 여우일 것이다" 라는 추론이 가능하다. 그렇기에 "학습과 추론도를 평가 하는 지표" 정도로 생각하는게 좋을 것 같다고 말한 것이다.

연산량에 따른 정확도

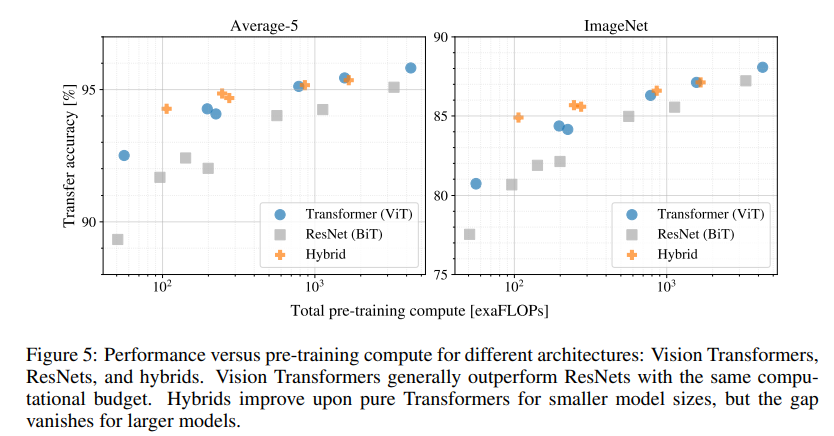
본문에서도 언급한 하이브리드가 이 곳에 다시 나왔다. Hybrid Architecture 는 Patch + Position Embedding 대신, CNN 으로 추출한 raw image 의 feature map 을 활용할 수 있는 방식이라고 설명했다.

Hybrid 방식은 pre-training 의 적은 연산부터 정확도가 높은 것을 보이고 있다. 하지만 결국 연산량이 많아졌을 때, Hybrid 방식과 일반 ViT 의 정확도는 차이가 없는 것도 같이 볼 수 있다. Hybrid 방식 굳이 사용할 필요가 없다는 말이기도 하다.

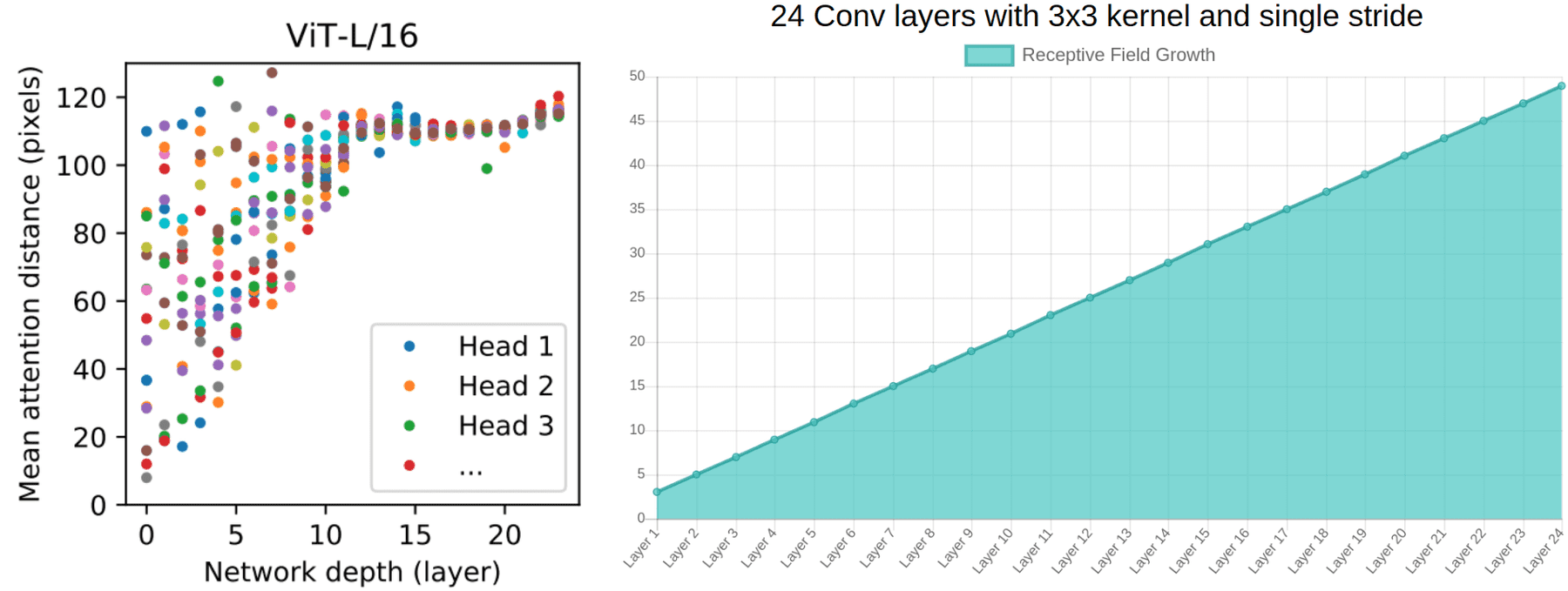
Global aspect

위의 좌측 이미지는 ViT 모델에서 사용하는 MSA 연산에 대한 부분이다. 첫번째 layer 부터 몇 몇개의 head 들이 이미지를 global 하게 본다는 것을 알 수 있다.

반면, 우측 이미지는 Convolution 연산을 사용하는 모델 지표다. Convolution 은 layer 가 높아짐에 따라 이미지를 global 하게 본다는 것 또한 알 수 있다. Convolution 의 특성에 입각한 결과이므로 당연한 지표다. 여기에서 다시한번 inductive bias 가 언급된다.

목차로 돌아가기

---

ViT 의 구조

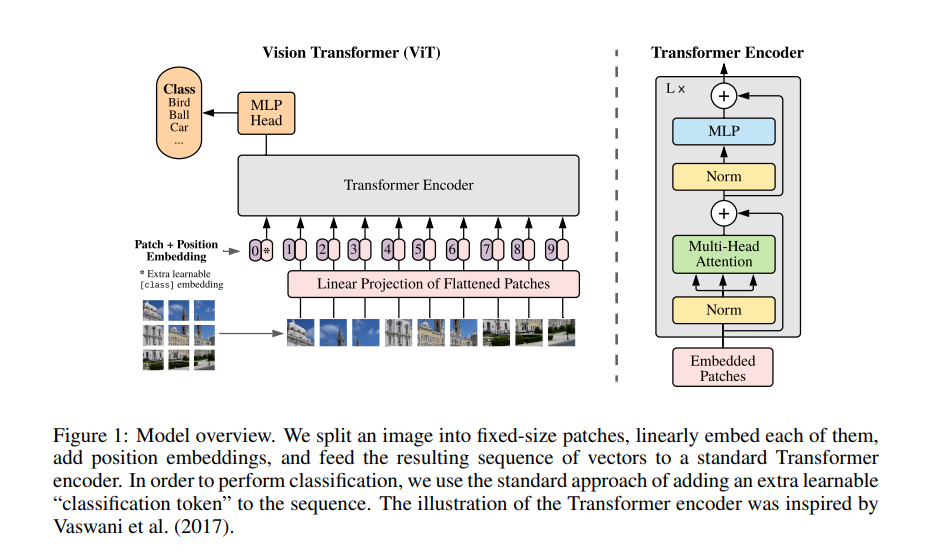
이미지를 패치단위로 나눠 임베딩 한 후 트랜스 포머 인코더를 거쳐 패치들간의 관계를 학습한 후, MLP Head 로 최종분류를 한 후 결과를 출력한다. 또한 CNN 으로 추출한 raw image 의 feature map 을 활용하는 Hybrid Architecture 로도 사용할 수 있다. 이 Hybrid Architecture 를 사용하면 뒤에 설명할 Patch+Position Embedding 과정을 생략할 수 있다.

본문 들어가기 전에..

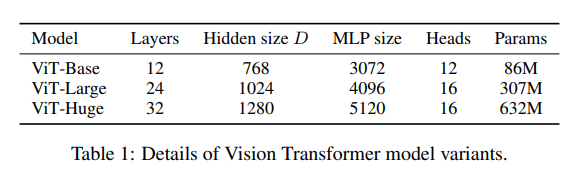
ViT/B-14, ViT/L-16, ViT/L-32, ViT/H-14, ViT/H-32

Vision Transformer 에는 "ViT/@-#" 와 같은 포맷으로 사용자가 하이퍼파라미터를 정한다. "@" 자리는 모델의 사이즈를 의미한다( Params 의 수에 의해 모델의 사이즈가 변경됨 ). 그리고, "#" 자리는 14, 16, 32와 같은 수가 오며, 사진을 자를 패치 사이즈를 의미한다(예를들어 16일 때, 패치 픽셀수는 $16\times16$ 이 된다).

"@" 자리에는 B(Base), L(Large), H(Huge) 가 들어가며, 위의 표( Table 1 ) 에 명시되어 있듯이 각각 다른 Layers, Hidden size D, MLP size, Heads, Params 를 갖는다.

ViT 의 전체적인 Flow

gif 클릭시 원본 저장소로 이동합니다

1. 패치 분할

위와 같이 사진을 조각내고 이 조각난 하나의 사진 단위를 패치라고 부른다

$x \in \mathbb{R}^{H \times W \times C}$

(이미지의)
$H$ : 높이 픽셀
$W$ : 넓이 픽셀
$C$ : 채널 수 (대체로 RGB 값)

위에서 $H \times W$ 는 사진의 해상도라고 생각하면 된다.

목차로 돌아가기

2. Flattened Patches

$X_p \in \mathbb{R}^{N \times (P^2 \cdot C)}$

$N$ : 패치의 개수 ( $\frac{HW}{P^2}$ )
$P$ (하이퍼 파라미터) : 패치의 가로 세로 픽셀 사이즈
( 즉, $P^2$ 은 패치의 해상도 )

• P(패치크기)는 보통 14×14, 16×16 또는 32×32로 선택되며, P가 작을수록 시퀀스가 길어져 연산 비용은 높아지지만 모델의 정확도는 향상된다
• 그래서 그런지 논문의 제목도 "An Image is Worth 16X16 Words" 이다.

$x_p^1$ 부터 $x_p^N$ 까지 계산되어서 아래와 같은 벡터화 수식이 만들어진다.

$x_p^1 \in \mathbb{R}^{P^2 \cdot C} \quad \ldots \quad x_p^N \in \mathbb{R}^{P^2 \cdot C}$

목차로 돌아가기

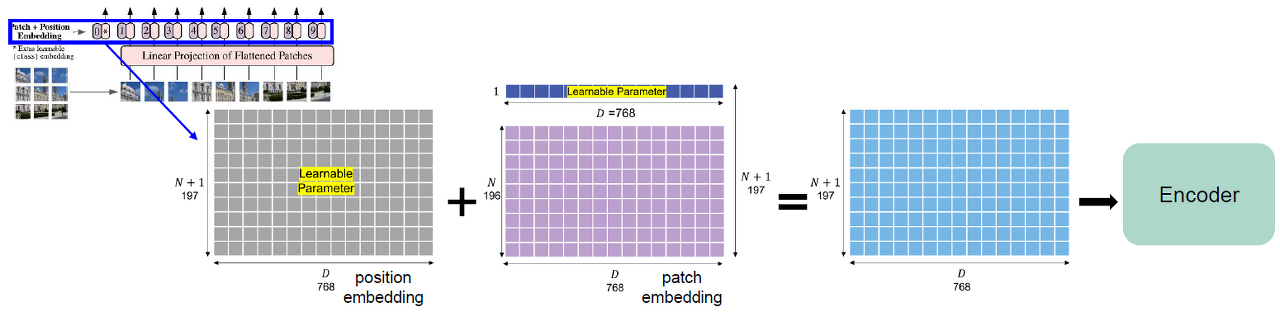
3. Patch + Position Embedding

$z_0 = [\mathbf{x}_{\text{class}}; \mathbf{x}_p^1\mathbf{E}; \mathbf{x}_p^2\mathbf{E}; \ldots; \mathbf{x}_p^N\mathbf{E}] + \mathbf{E}_{\text{pos}}$

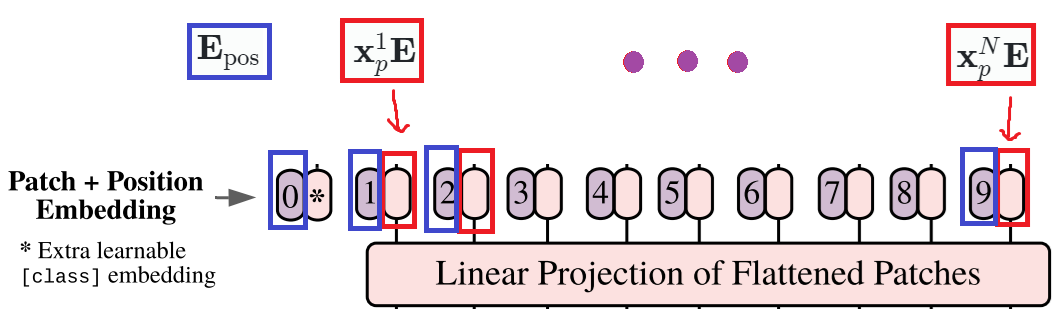
$z_0$ : 시퀀스 ( Transformer encoder 의 input 재료 )

• 위에 보이는 0* 는 자리에 classification token 이 들어가며 기호로는 $\mathbf{x}_{\text{class}}$로 표시한다.
• classification token은 이미지 전체에 대한 정보이며, 이 토큰은 이미지 패치들과 함께 트랜스포머 모델에 들어간다.
• BERT의 [CLASS] token 과 유사하다고 보면 된다.
• 위 시퀀스 $z_0$ 는 $z_\ell$ 와 같이 layer 의 개 수만큼 생성된다고 보면 되겠다

3-1. Linear Projection ( Patch Embedding )

$\mathbf{E} \in \mathbb{R}^{(P^2 \cdot C) \times D}$,

$D$ : 일정한 잠재 벡터 크기 (constant latent vector size)
$E$ : 학습된 임베딩 행렬 (learned embedding matrix)

각 패치마다 Linear Projection 을 하게 되며, Patch Embedding $(\mathbf{x}_p^1\mathbf{E}\ldots\mathbf{x}_p^N\mathbf{E})$ 가 만들어진다.

3-2. Position Embedding

$\mathbf{E}_{\text{pos}} \in \mathbb{R}^{(N+1) \times D}$

$E_{pos}$ : 패치의 위치(Position) 정보

Position Embedding은 각 패치의 위치정보를 기억하기 위해 사용한다. 그리고 시퀀스화된 패치의 위치 정보를 위해 수식의 끝에 추가가 된다.

$\mathbb{R}^{(N+1) \times D}$ 에서 $N$ 에 $+1$이 왜 붙었어요 ?

왜 $\mathbb{R}^{N \times D}$ 이 아니냐고 물어볼 수 있다. 하지만 임베딩된 패치들의 맨 앞에 학습가능한 임베딩 (class token $z_0^0 = \mathbf{x}_{\text{class}}$) 이 존재하기 때문에 '$+1$' 을 추가하는 것이다. 즉, classification token 도 포함되어야 하기에 추가되었다고 보면 된다.

참고 )

아래 이미지는 어떤 식으로 embedding 하는지 잘 보여주는 것 같아서 가져왔습니다.
( 이미지 클릭시 원본 블로그로 forwarding 됩니다. )

Embedding (P=16, H=W=224, N=196, D=768)

• 가장 첫번째 패치 임베딩 앞에 학습 가능한 임베딩 벡터를 붙여줌. 이는 추후 이미지 전체에 대한 표현을 나타내게 됨.
• N+1개의 학습 가능한 1D 포지션 임베딩 벡터 (이미지 패치의 위치를 특정하기 위함)를 만들어준 후, 이를 각 이미지 패치 벡터와 합해줌. (두 Matrix의 합)
• 만들어진 임베딩 패치를 Transformer Encoder에 입력으로 넣어줌.

목차로 돌아가기

4. Transformer Encoder

$\mathbf{z}^{\prime}_\ell = \text{MSA}(\text{LN}(\mathbf{z}_{\ell-1})) + \mathbf{z}_{\ell-1}, \quad \ell = 1 \ldots L$

$\mathbf{z}_\ell = \text{MLP}(\text{LN}(\mathbf{z}^{\prime}_\ell)) + \mathbf{z}^{\prime}_\ell, \quad \ell = 1 \ldots L$

$\mathbf{y} = \text{LN}(\mathbf{z}_L^0)$

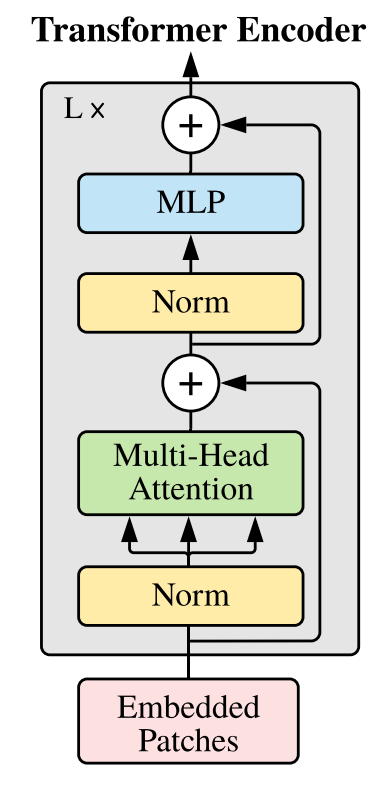
• $\ell$ 은 layer 를 표현하는 기호

• Transformer Encoder 는 크게 Multi-Head Attention 과 MLP blocks 로 구성된다.
• Multi-Head Attention 와 MLP 전에 LayerNorm(LN) 을 적용한다.
• Transformer Encoder 는 패치간의 관계를 파악하기 위해, self-attention 메카니즘을 활용해서 패치간의 관계를 학습하고, 이미지를 global 하게 파악한다.
• Skip Connection 기법을 통해, Multi-Head Attention 를 통과한 output 과 통과하지 않은 기존 값을 더해 기존 값을 유지한다. 위 이미지의 위 이미지의 + 부분을 residual connection 이라고 한다.
• 다시 한번 Skip Connection 기법을 통해, MLP block 을 통과한 output 과 기존 값을 더해줘서 최종 output 을 출력한다.

또한, 위 아키텍처에서의 Norm (LayerNorm) 과 ViT 이전의 Transformer Model(Vanila Transformer) 은 조금 다른 점이 있다. 기존의 Transformer Model 에서의 Norm 은 LayerNorm 이 아닌 BatchNorm 이었고, Norm 의 위치가 MSA의 위치, MLP의 위치에 있었다. 그러나 Norm 의 위치를 이와 같이 바꾸니 퍼포먼스가 좋아졌다고한다.

Batch vs Layer Normalization

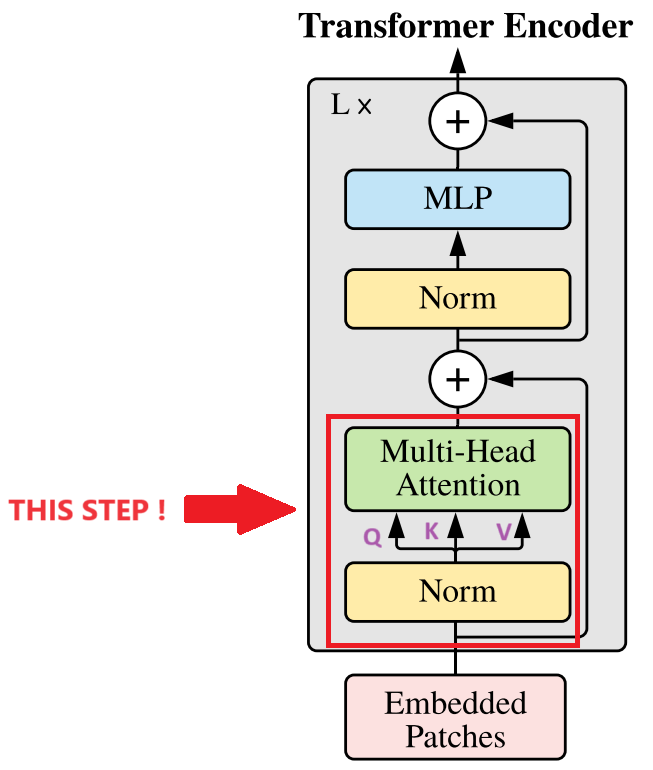
4-1. Multi-Head Attention ( MSA )

MSA 는 MHA 라고도 불리우는 것 같지만 이 글에서는 MSA 라고 하겠다. 그리고 MSA에 대한 설명을 진행하기 전에, 내 글보다 더 좋은 글을 찾아서 공유하려고한다. 이 글은 ViT 에 대한 설명은 아니지만, Transformer 에 대한 전반적인 설명이 들어가 있는 좋은 글이다.
Transformer 파헤치기 - Multi-Head Attention

$\mathbf{z}^{\prime}_\ell = \text{MSA}(\text{LN}(\mathbf{z}_{\ell-1})) + \mathbf{z}_{\ell-1}, \quad \ell = 1 \ldots L$

$MSA$ : Multiheaded Self-Attention
$LN$ : Layer Normalization

$\mathbf{z}^{\prime}_\ell$ 을 구하는 수식을 풀자면 아래와 같다

$[q, k, v] = zU_{qkv}, \quad U_{qkv} \in \mathbb{R}^{D \times 3D_h}$

$A = \text{softmax}\left(\frac{q\cdot k^T}{\sqrt{D_h}}\right), \quad A \in \mathbb{R}^{N \times N}$

$SA(z) = A\cdot v, \quad A\cdot v \in \mathbb{R}^{N \times D_h}$

Self-Attention for MSA 아래 참고부록으로..

$MSA(z) = [SA_1(z); SA_2(z); \ldots; SA_k(z)]U_{msa}, \quad U_{msa} \in \mathbb{R}^{k \cdot D_h \times D}$

$k$ : 'head' 의 개수
$U$ : 변환 행렬 ( transform matrix )

Multi-Head Attention ( MSA ) 은 Transformer 의 Self-Attention 에 해당하는 부분으로 패치 간 관계를 파악하는 부분이다. CNN에서 볼 수 있는 지역적인 연관성( locality )과 같은 inductive bias가 상대적으로 적어, 전체 이미지의 특징(global features) 을 파악하는 데 있어 효과적이다. 하지만, MSA 는 ViT 모델을 떠나 Transformer 기반 모든 모델에서 연산량이 가장 많이 요구되는 부분이기도 하다.

MSA 는 'head' 의 개수만큼 독립적인 SA 를 갖고있고, 각각의 head 가 SA 를 병렬로 계산한다. 그러므로, MSA는 여러 'head' 들이 각각 주어진 SA의 Query, Key, Value 행렬을 계산하고, Attention 가중치를 병렬로 계산한다. 그리고, 이 가중치들은 최종적으로 concat 되어서 통합된 인사이트를 제공해준다.

추가로 위 수식 $\mathbb{R}^{k \cdot D_h \times D}$ 을 덧붙여 말하자면, $SA$ 연산을 수행하면 차원이 줄어든다. 그렇기에 $\mathbb{R}^{k \cdot D_h \times D}$ 에서 $k\text{(head 의 개수)}$ 가 곱해진 것이다. 이로써, $SA$ 연산으로 줄어든 차원이 복구된다.

QKV ( query, key, value ) ?

INDUCTIVE BIAS

4-2. MLP ( Multi-Layer Perceptron ) aka. FFN(Feed-Forward Network)

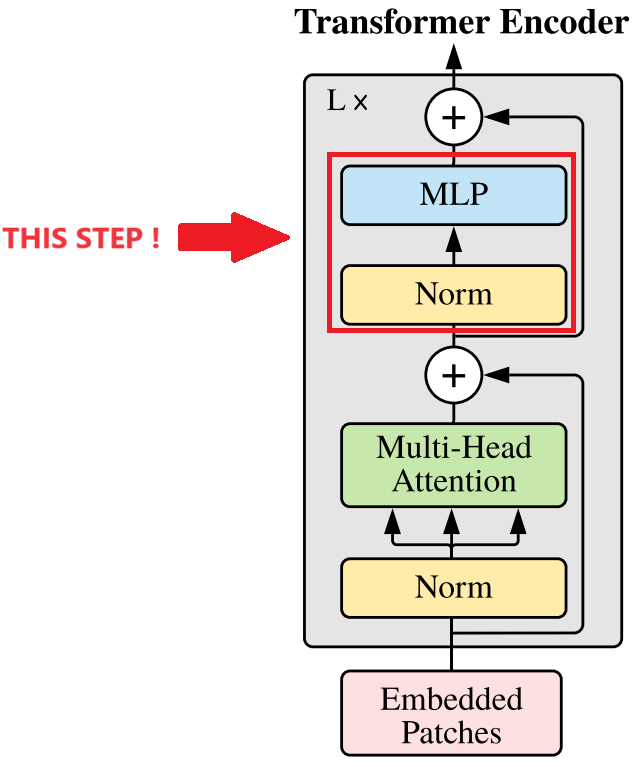
MLP is a two-layer classification network with GELU (Gaussian Error Linear Unit) at the end. The final MLP block also called the MLP head, is used as an output of the transformer. An application of softmax on this output can provide classification labels (i.e., if the application is Image Classification).

-v7labs.com

번역기 번역본↓
MLP는 마지막에 가우스 오차 선형 단위(GELU)가 있는 2계층 분류 네트워크입니다. MLP 헤드라고도 하는 최종 MLP 블록은 트랜스포머의 출력으로 사용됩니다. 이 출력에 소프트맥스를 적용하면 분류 레이블을 제공할 수 있습니다(예: 애플리케이션이 이미지 분류인 경우).

$\mathbf{z}_\ell = \text{MLP}(\text{LN}(\mathbf{z}^{\prime}_\ell)) + \mathbf{z}^{\prime}_\ell, \quad \ell = 1 \ldots L$

$\mathbf{y} = \text{LN}(\mathbf{z}_L^0)$

여기서 ViT 이전의 Transformer 와는 다른 점이 전에는 활성화 함수로 ReLU 를 사용했지만, ViT 에서는 GELU 를 사용하는 것을 볼 수 있다.

MLP 는 2개의 FC layer 갖고, 그 사이에는 GELU ( Gaussian Error Linear Unit ) 활성화 함수 ( Activation function ) 가 실행된다.

1. MLP 내의 실행 순서는 첫 번째 FCLayer 가 차원을 확장시켜서 더 많은 데이터를 학습할 수 있는 공간을 만든다.
2. GELU 활성화 함수로 확장된 차원에 대한 벡터를 비선형적으로 변환. 이 과정에서 입력벡터와 입력벡터의 누적 정규분포의 곱으로 계산된다. 이 활성화 함수로 복잡한 패턴을 더 잘 이해할 수 있다.
3. 두 번째 FCLayer 가 출력 형태를 맞추기위해 원래 차원으로 복구한다. 위의 중요한 정보를 요약하고 압축한다.

마지막으로, 위 아키텍처 이미지 어디에도 보이지는 않지만, 수식 $\mathbf{y} = \text{LN}(\mathbf{z}_L^0)$ 을 보아하니 MLP 이후에도 LayerNorm 으로 한번 더 감싸주는 것으로 보인다. 이 것이 L 번 반복된 후 최종 출력은 $z^L_L$ 으로 출력된다.

목차로 돌아가기

5. MLP Head

ViT 아키텍처의 마지막 부분으로 최종 이미지 분류를 시행한다.

Pretraining 단계

• 대량의 이미지 데이터셋을 통해 학습됨
• Transformer Encoder 에서 나온 output 을 [CLASS] Token 을 이용해서 이미지가 어떤 카테고리인지 분류함

Fine-tuning 단계

• 특정 목적에 맞게 MLP Head 내의 구성을 변경할 수 있음
• pretraining 단계에서 학습된 가중치를 바탕으로 더 작은 데이터 셋에 맞게 조정 됨
• MLP Head 대신 간단하게 linear layer 를 사용하기도 함

목차로 돌아가기

---

DiTs: ViT 그 이후 연구...

ViT 가 발표된 후, Transformer 를 사용한 이미지 분류는 새로운 형태로 여러 발전과정을 거쳤고 현재도 계속 발전되고 있다( swin transformer, ViT-Adapter, DiTs, Masked Diffusion Transformer, 등 등). 그리고 여기서 사용한 Diffusion 과 Transformer 를 결합한 DiTs ( 논문 본 제목 : Scalable Diffusion Models with Transformers ) 는 ViT의 아이디어를 더욱 발전시켜, 이미지의 공간적 표현을 기반으로 한 확산 모델에 트랜스포머 아키텍처를 적용한 모델이다. 아직 정확하지 않지만, 떠도는 말로는 DiTs가 현재 sora 의 기반이 되는 모델이라고 한다.

목차로 돌아가기

---

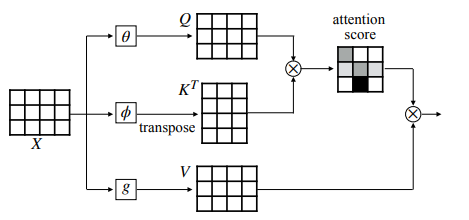
Self-Attention for MSA

아래 설명은 MSA 에서의 SA 를 설명하기 위한 보충 설명이며, 일반적인 SA 와는 조금 상이한 부분이 있습니다.

$[q, k, v] = zU_{qkv}, \quad U_{qkv} \in \mathbb{R}^{D \times 3D_h}$

$A = \text{softmax}\left(\frac{q\cdot k^T}{\sqrt{D_h}}\right), \quad A \in \mathbb{R}^{N \times N}$

$SA(z) = A\cdot v, \quad A\cdot v \in \mathbb{R}^{N \times D_h}$

• $D_h= \frac{D}{k}$ ( 왼쪽의 $k$ 는 위의 $k(key)$ 가 아니라 attention head 의 개수를 의미한다)
• $A$ 는 Attention Score
• $k^T$ 의 $T$는 Transpose 는 전치를 의미하며 행으로 늘어선 배열과 열로 늘어선 배열의 내적을 구하기 위함이다.
  • TMI ) 수학적 표현으로 벡터의 내적은 일(W)를 구하기 위해 사용된다.
• $SA$ 는 Self-Attention
• $v$ 는 Query, Key, Value 에서의 Value(v)

위의 수식은 MSA 수식이다. Single Self-Attention 에서는 $D_h$ 가 사용되지 않는다. 왜냐하면 단일 헤드기 때문이다. 하지만 이 보충설명은 MSA 를 위한 SA 메커니즘 설명이다. 단일 Self-Attention 메커니즘으로만 놓고보면 수식은 아래와 같다.

$Attention(Q,K,V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$
$d_k$ 는 key 의 차원 수를 말한다.

$\mathbb{R}^{D \times 3D_h}$ 에서 $D \times 3D_h$

$D_h$( $\frac{D}{k}$ ) 는 헤더들이 수행해야하는 총 수행량이라고 보면 되고, 그 앞의 3은 세 군데(각 q,k,v) 전부에 대한 연산을 해야함 암시한다. 마지막으로 $D$ 는 위에서 언급한 것들이 총 Dimension 에 대해 연산이 수행되어야 함을 의미한다.

$q = z \cdot w_q, \quad w_q \in \mathbb{R}^{D \times D_h}$

$k = z \cdot w_k, \quad w_k \in \mathbb{R}^{D \times D_h}$

$v = z \cdot w_v, \quad w_v \in \mathbb{R}^{D \times D_h}$

$[q, k, v] = z \cdot U_{qkv}, \quad U_{qkv} \in \mathbb{R}^{D \times 3D_h}$

$\text{softmax}\left(\frac{q\cdot k^T}{\sqrt{D_h}}\right)$

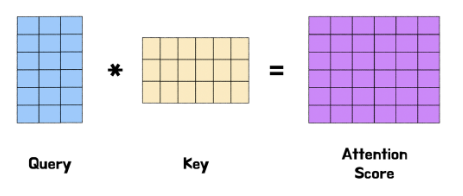
$q\cdot k^T$ 는 $q$, $k^T$ 두 벡터의 행렬곱이자 "행렬 벡터의 내적" 이다. 또한, 내적( 행렬곱 )을 사용하는 이유는 벡터 행렬간의 유사도를 계산하기 위함이다. 머신러닝에서는 두 벡터의 내적을 통해 유사도를 계산하는 것은 일반화 되어있다( 코사인 유사도와 같이 언급됨 ).

위 이미지를 보면 Key 가 이미 Transpose( 전치 ) 되어 있는 상태로 행렬곱이 되었다. 이는 내적을 계산하려면 두 벡터의 차원이 일치해야 하기 때문이다.

왜 차원이 일치해야하는지, 행렬곱의 특성에 대해 알고있다면 바로 수긍 가능하다.

여기 A와 B라는 행렬이 있다. A와 B 는 각각 아래와 같은 행과 열을 갖는다.
$A=m\times{n}$
$B=p\times{n}$

에서, $A\times{B}$ 는 성립할 수가 없다. 그래서 우리는 B를 전치해서 아래와 같이 만들어 줘야한다.

$A=m\times{n}$
$B^T=n\times{p}$

$A\times{B^T}=m\times{p}$

$\sqrt{D_h}$ 로 $q\cdot k^T$ 내적을 나눠주는 이유는 내적의 결과를 안정적으로 만들기 위함이다. 즉, $\sqrt{D_h}$ 는 내적의 결과를 스케일링 해주는 값이다. 이 스케일링을 통해 그라디언트가 과도하게 커지거나 작아지는 것을 방지한다.

$softmax$ 는 위 연산을 거친 점수들을 확률적으로 변환시킨다. 그리고 output 은 'Attention Weights' 라고도 불리운다. 즉, 각 입력에 대한 출력의 가중치를 의미한다. 이 과정을 거치면 Attention Score 의 유사도는 0 ~ 1사이가 된다.

마지막으로 여기 softmax 를 거쳐서 나온 Attention Score 에 Value(v) 를 곱하면 Self-Attention ( $SA$ ) 이 된다.

본문으로 돌아가기

목차로 돌아가기