🔸회귀분석(Regression Analysis)

회귀분석

• 회귀: 하나 혹은 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법

• 선형회귀: 학습 데이터를 통해 어떤 임의의 점이 평면 상에 그려졌을 때 최적의 선형 모델을 찾는 것을 목표로 함.

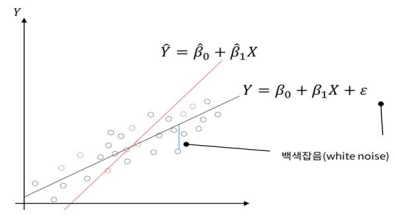
• 단순 선형 회귀분석
  

• 검은 점: 모집단의 모든 데이터 / 빨간 점: 학습집합의 데이터
  (모집단의 모든 데이터 분석 어려워, 학습집합 분석 후 잔차를 통해 추정)

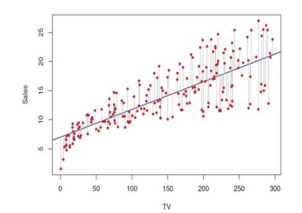
• 최적의 회귀 모델: 전체 데이터의 잔차(오류값)의 합이 최소가 되는 모델
  -> 오류값이 최소가 되는 회귀계수(절편, 기울기) 찾기

오차 계산

• 잔차(residual) : 실제값 - 추정값
  

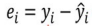
• 잔차의 제곱합(SSE; Error Sum of Squares)
  

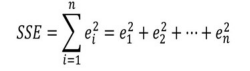
• 잔차의 제곱합을 최소화하는 이유 :
  1) 잔차의 합이 0이 되는 해는 무수히 많음 (유일한 해 X)
  

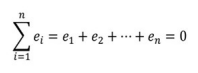
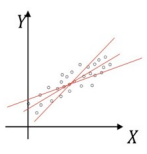
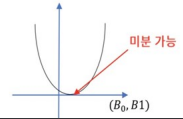
2) 잔차의 절대값의 합은 미분 불가능

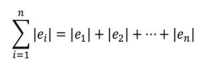
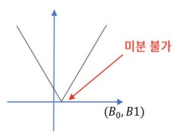
3) 잔차의 제곱합 -> 유일한 해O, 미분 가능O

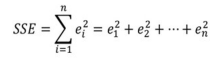
경사하강법

• 고차원 방정식에서 RSS가 최소가 되는 직관적 방법 제공
  -> 비용함수가 최소가 되는 W 변수값 효과적으로 도출
  
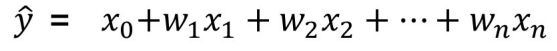
  방법:
  
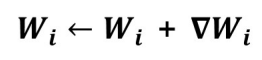
  제곱합(Squared Loss):
  
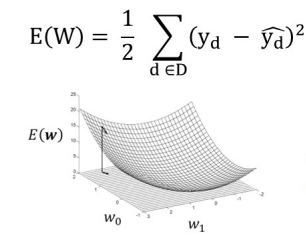
  평균제곱합(Mean Squared Loss):
  
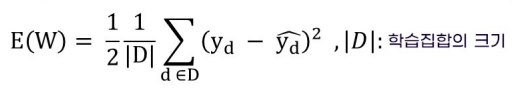
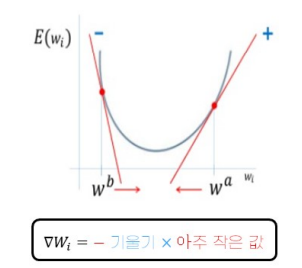
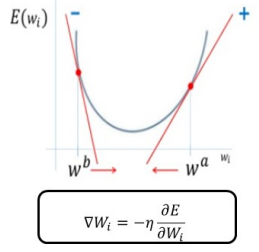
  W 파라미터 업데이트: 그래디언트 반대방향(-), 즉 '-기울기'
  
  
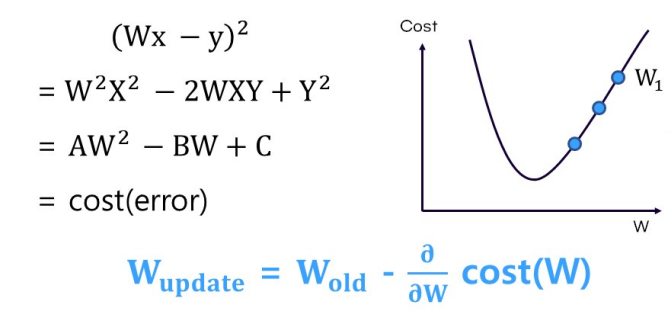
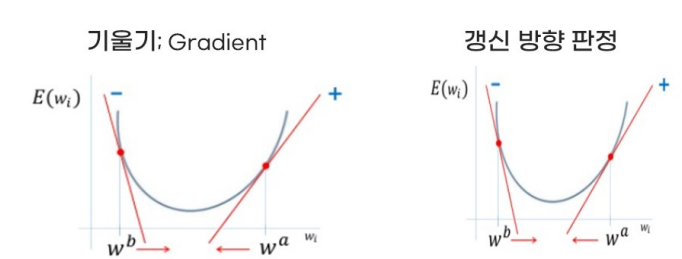
  갱신 크기 결정(learning rate): 아주 조금씩 갱신되도록 함.
  
  

코드실습

scatter plot 시각화

import numpy as np
import matplotlib.pyplot as plt 
%matplotlib.inline 

np.random.seed(0) 
X = 2 * np.random.rand(100, 1) 
y = 6 + 4 * X + np.random.randn(100,1) # 노이즈 생성을 위해 random값 추가


plt.scatter(X,y)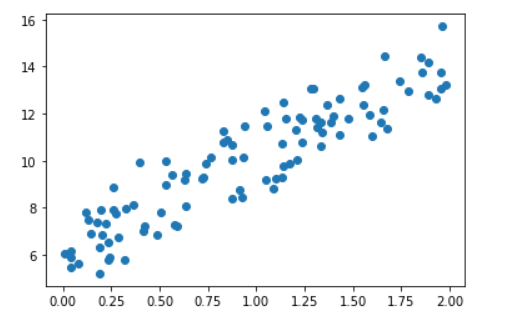

w1,w0 업데이트

# w1, w0 업데이트를 위한 w1_update, w0_update 반환
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
    N = len(y) # y=w0+w1X1(즉, 벡터의 길이)
    # 먼저 w1_update, w0_update를 각각 w1, w0의 shape과 동일한 크기를 가진 0 값으로 초기화
    w1_update = np.zeros_like(w1) 
    w0_update = np.zeros_like(w0)
    y_pred = np.dot(X, w1.T) + w0 # dot 연산 시, y = ax+b ax->np.dot(X,w1.T)
    diff = y-y_pred # error function  = (실제값 - 예측값)
         
    # w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진 행렬 생성 
    w0_factors = np.ones((N,1)) 

    # w1과 w0을 업데이트할 w1_update와 w0_update 계산
    w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff)) # error ftn : mse(mean square error)
    #/summation_i^n (y-y_hat)(-x_i)
    w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff)) # summation_i^n (y-y_hat)(-x_1)
    
    return w1_update, w0_update #W_0,W_1 update

# iters 횟수만큼 반복적으로 w1, w0 업데이트 
def gradient_descent_steps(X, y, iters=10000):
    # w0, w1 모두 0으로 초기화 
    w0 = np.zeros((1,1))
    w1 = np.zeros((1,1))
    
    # iters 횟수만큼 반복적으로 get_weight_updates() 호출하여 w1, w0 업데이트 
    for ind in range(iters):
        w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
        w1 = w1 - w1_update # new = old - update (update = 0->new =old ) 
        w0 = w0 - w0_update
              
    return w1, w0

def get_cost(y, y_pred):
    N = len(y) 
    cost = np.sum(np.square(y - y_pred))/N
    print(cost) # root(실제값-예측값) 합산해서 저장-> cost
    return cost

w1, w0 = gradient_descent_steps(X, y, iters=1000) #1000번 반복
#최적의 값과 그때의 cost값 출력
print("w1:{0:.3f} w0:{1:.3f}".format(w1[0,0], w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))

plt.scatter(X, y)
plt.plot(X,y_pred)