💻이번 포스팅에서는 가설검정절차를 암기하는 것에서 벗어나 가설검정의 논리를 이해하고 검정에 관련된&헷갈리는 개념 정리 및 이를 바탕으로 성공적인 A/B테스트를 위해서는 어떤 점을 유의해야 하는지 정리해보았다!
🔎가설 검정 논리
- 가설검정의 목적은 새로운 자료(D)가 수집되었을 때, 이 자료(D)가 이미 알고 있는 분포(H)로부터 나왔는지 그렇지 않은지를 판단하는 것이다.
- 먼저 자료가 H분포에서 나왔다고 가정한다.
- 분포를 가정하면 자료(D)가 H분포에서 나왔을 확률을 계산할 수 있다. P(D|H)를 계산한다.
- 이 확률이 아주 낮으면, 아마도 자료 D가 H분포에서 나오지는 않았을 것이라고 결론 내린다. 확률이 아주 낮지 않으면, 결론을 유보한다.
EX)
1. 새로운 진통제를 개발하고 이 진통제의 지속시간을 측정하니 9시간이었다. 이 진통제의 지속시간이 기존 진통제의 지속시간 분포에서 나왔는지, 그렇지 않으면 기존 진통제와는 다른 분포에서 나왔는지(기존의 진통제보다는 지속시간이 긴지)를 검증하고 싶다.
2. 이 9시간이라는 지표가 평균이 5이고 표준편차가 2인 정규분포를 따르는 기존 진통제 분포에서 나왔다고 가정하자.
3. 이때 진통시간 9시간이 기존의 진통시간 분포인 N(5,2^2)에서 나왔을 확률을 계산할 수 있다.
4. 만약 이 확률이 우리가 기준으로 정한 확률보다 낮으면, 기존의 분포에서 이 자료가 관찰될 확률이 아주 낮으므로 기존 분포에서 나왔다는 가정을 기각한다. 즉, 새로운 진통제의 효과는 기존의 효과와는 다르다고 결론을 내릴 수 있다. 그렇지 않으면 결정을 유보한다.
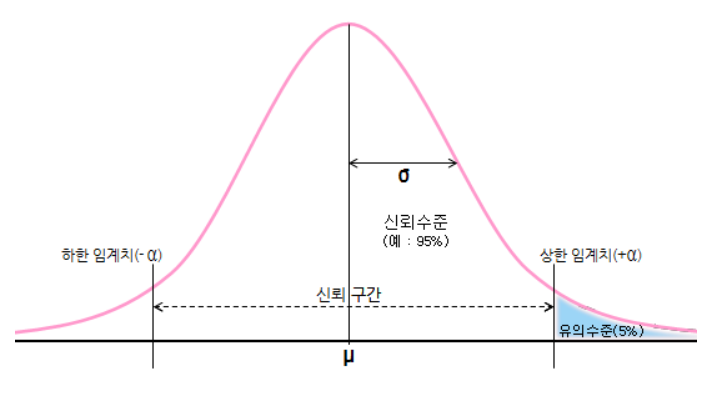
📌 신뢰구간과 유의수준
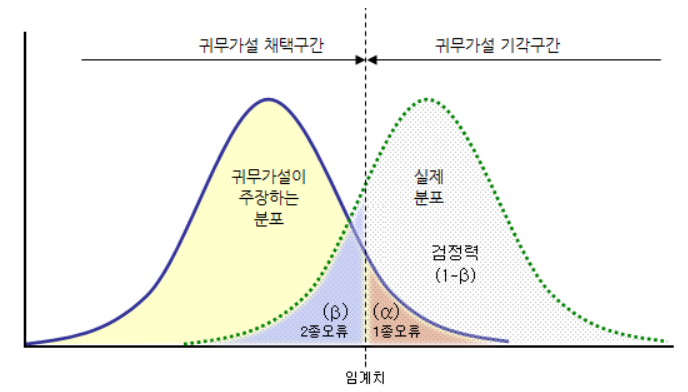
📌1종오류, 2종오류, 검정력
-
α=유의수준=P(h0기각|H0이 참)
⭐유의수준=0.05의 의미
= 주어진 검정방법을 계속 시행했을 경우, 귀무가설이 참이라는 전제하에 5%정도 옳지 않다는 판단을 내리게 됨.
- 귀무가설이 참일 때 이를 기각할 확률= 차이가 없을 때 차이가 있다고 결정할 확률
= 표본을 추출해서 나온 검정통계량이 우연히 나타날 확률이 5%미만이다.
*우연에 의한 결과이다 = 유의한 차이가 없다 -
β=P(h0기각|H0 거짓)
-
검정력(power) = P(H0기각|H0거짓)=1-β
➡ 신뢰구간이 커질수록 유의수준(α) 낮아진다.
➡ 유의수준(α)을 낮게 설정할수록 귀무가설 기각이 어려워짐.
📌p-value
= probability-value의 줄임말. 어떤 사건이 우연히 발생할 확률을 의미.
-
p-value=P(Data|H0)=귀무가설이 참일 때 자료가 발생할 확률
= 귀무가설이 참이라는 전제 하에, 관찰된 검정통계량 값이 관찰될 확률 -
p-value >α 의미: 1종오류를 범할 가능성이 커졌다고 간주.
⭐ p-value<α 의 경우 기존 분포에서 이 자료가 관찰될 확률이 아주 낮음을 의미하므로 H0 기각
⭐"95% 신뢰수준에서 A조건의 클릭율이 B조건의 클릭율보다 유의미하게 높다"의미
≠A조건의 클릭율이 B조건의 클릭율보다 높을 확률이 95%
= A조건의 클릭율이 B조건의 클릭율과 차이가 없다고 가정했을 때 이 분포에서 극단적인 검정통계량이 관찰될 확률(p-value)은 5% 미만⭐ α가 p-value보다 커야 기각이었나? p-value보다 작아야 기각이었나?라고 헷갈린다면?
α가 무슨 의미였는지에 대한 개념을 다시 생각해보자. 가설검증의 전제는 모두 H0가 참이 전제였다. 이에 α는 H0가 참인데 기각해버릴 확률이었다.
🔎가설검정 절차
STEP 1. 가설의 수립과 α수준의 결정
- 귀무가설이 평균의 형태로 기술된다고 해도, 실제 의미는 분포에 대한 가설이다.
- α수준 = 가설검증의 절차에서 관찰된 자료가 귀무가설에서 나왔을 확률이 낮으면 귀무가설을 기각한다. 어느정도 낮아야 귀무가설을 기각할 것인지에 대한 기준.
⭐귀무가설(H0)과 대립가설(H1)의 원칙.
- 등호가 붙는 가설이 귀무가설이다. H0가 참이라는 가정하에 검정통계량 분포를 구하는 논리로 진행된다.
⭐귀무가설의 특징
- 효과없음, 차이없음의 의미를 내포하는 가설이다.
- 귀무가설은 분포에 대한 정의가 선행되어야 한다.
EX) A제품과 B제품의 만족도점수에 대한 유의미한 차이가 있을까? H0은 무조건 차이가 '없다'로 설정하는 것이 옳음.(선택 사항이 아님)
확률변수 X를 진통제의 지속시간이라고 정의하면 H0: X ~N(5,2^2)이지만
보통 검증하고자 하는 것은 평균에 대한 가설이므로
- H0:μ=5
- H1:μ≠5
STEP 2. 자료가 관찰될 확률의 계산
- 계산할 확률은 관찰된 자료 9가 귀무가설의 분포에서 나왔을 확률이다.
X가 9보다 클 확률은 다음과 같이 계산된다.
= P(Z>2)=0.02275
STEP 3. 의사결정
- 귀무가설이 참이라는 전에 하에 검정통계량이 관찰될 확률이 유의수준보다 작을 때 귀무가설을 기각한다.
- X가 9보다 클 확률이 α수준보다 낮으므로 귀무가설 기각한다.
- 즉 신약은 기존의 지속시간보다는 길다고 결론을 내릴수 있다.
🔎A/B 테스트 설계 시 유의사항
💡실험 집단과 통제 집단 샘플링
- 통제변수 관리가 잘 되지 않은 상태에서는 랜덤추출이라고 할 수 없다.
- 랜덤추출은 통제변수가 잘 관리된 것을 전제로 모든 표본이 동일한 확률을 가진 상태에서 뽑는 무작위 추출을 의미
회원번호를 단순 홀/짝으로 나누어 실험집단을 구분한 것을 랜덤샘플링이라고 하기 어려운 이유
- 두 개의 추천알고리즘 중 어떤 것이 더 효과적인지 알아보려고할 때 홀수번호 고객의 여행목적이 '비즈니스'인 경우가 많고 짝수번호 고객의 여행목적이 '휴양'인 경우가 많았다면 이에 대한 결과를 신뢰할 수 있을까?
💡샘플크기
- 가설을 검증하려면 어느 정도의 샘플 수가 필요할까? 샘플 크기는 실험을 하기 전 미리 설정해야 한다.
- 일반적으로 검증하고자 하는 가설, 검정력, 유의수준 등 실험 설계 조건 입력시 필요한 샘플 수 계산 사이트 존재
💡단순 평균값 비교
- A조건의 클릭율보다 B조건의 클릭율이 더 높으므로 B가 더 좋다고 말할 수 없는 이유
결과가 우연에 의해 나타난 결과일 수 있기 때문이다. 단순 평균이나 합계 지표의 차이는 샘플링 방법이나 실험 설계에 따라 결과가 달라질 수 있다.
💡엿보기+조기 중지
- A/B테스트에서 엿보기와 조기중지(peeking)란 실험을 진행하는 동안 계속 p의 값의 변화가 있음에도 중간에 갑자기 실험을 중단하는 것=> 어뷰징
💡시간의 흐름에 따른 차이를 살펴보지 않는 것
- A/B테스트 기간 전체에 대한 종속 변수 평균을 비교하는 것도 중요하지만 시간의 흐름에 따라 종속 변수가 어떻게 변화했는지를 보는 것도 중요.
- 실험 초기와 후기에 결과의 방향이 바뀌는 경우가 발생한다. 이 경우 실험 집단 샘플링에 실패했거나, 특정 시점에 기능 오류가 발생했거나, 데이터 수집 과정에서의 오류일 수 있으므로 실험과정을 시간의 흐름에 따라 재확인 필요
💡과거의 A/B 테스트 경험을 지나치게 신뢰하는 것
- 사용자층의 변화, 트렌드 변화 등 다양한 요인에 의해 A/B테스트 결과는 얼마든지 달라질 수 있다.
- 어제의 최적화는 오늘의 레거시일 수 있다
💡국지적 최적화의 함정
- A/B 테스트는 기본적으로 주어진 조건 안에서 성과비교 실험
- 애초에 A와 B라는 조건 자체가 최선이 아니었다면 A/B테스트의 임팩트 자체가 크지 않을 수도 있다.
Reference
-
사회과학을 위한 고급통계학(김청택, 학지사)
-
그로스해킹(양승화)
-
이미지) 1종오류,2종오류,검증력