EfficientNet

Rethinking Model Scaling for Convolutional Neural Network

• 본 리뷰에는 잘못된 내용이 있을 수 있으므로 유의하며 읽으시길 바랍니다.

논문: https://arxiv.org/abs/1905.11946

Introduction

기존에는 Convnet의 크기를 키우는 것(scaling up)은 더 높은 정확도를 얻기 위해 사용되었고,
깊이(depth) 혹은 너비(width)를 키우는 것이 가장 흔한 방법이었다.

이 논문은 기존 방법 보다 더 높은 정확도(accuracy)와 효율성(efficiency)을 달성할 수 있는
scaling up 방법을 다룬 논문이다.

논문에서는 network의 너비(width), 깊이(depth), 해상도(resolution)의 균형이 중요하다는 것을
실험을 통해 증명하였다.

network scaling은 baseline network에 영향을 많이 받기 때문에 neural network search를 통해 새로운 baseline network(EfficientNets)을 만들었다.

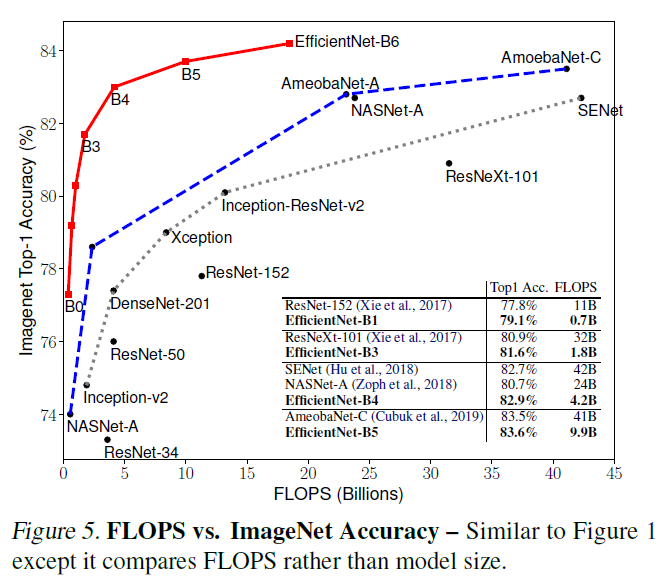
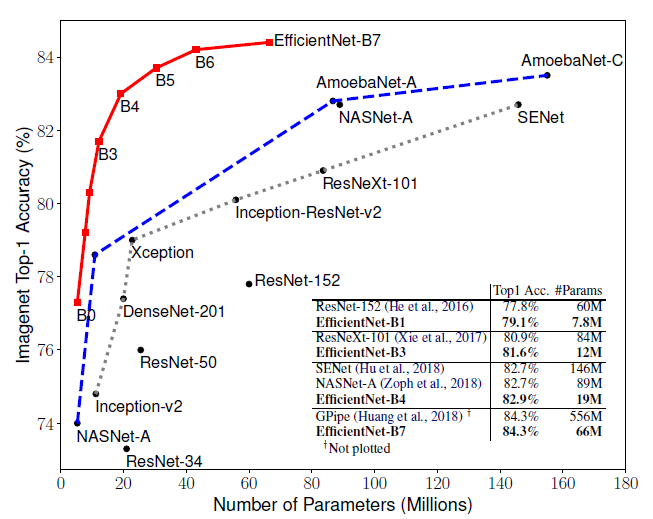
아래는 EfficientNet과 다른 network의 정확도와 parameter의 수를 비교한 그래프이다.
모든 면에서 EfficientNet이 앞서고 있음을 확인할 수 있다.

Related Work

• ConvNet Accuracy
  AlexNet을 이후로 network의 크기가 커질수록 정확도도 높아졌다.
  2014 ImageNet의 winner인 GoogleNet은 6.8M개의 parameter를,
  2017 ImageNet의 winner인 SENet은 145M개의 parameter를 가지고 있었고,
  2018 ImageNet에서는 557M개의 parameter를 가진 network가 우승을 하였다.
  이처럼 network의 규모가 커지게 되면서, 이를 처리하기 위한 별도의 작업이 필요했고, 하드웨어 메모리를 한계를 마주하게 되었다.
  그 결과 효율성에 대한 중요도가 높아지게 되었다.

• ConvNet Efficiency
  Model Compression은 효율성을 위해 network의 크기를 줄이는 한 방법이며,
  그리고 최근에는(논문기준) neural architecture search를 이용하여 network의 크기를 조절하는 방법이 큰 인기를 끌고 있다. 하지만 적용해야 할 범위가 더 넓어서 더 많은 비용이 드는 큰 모델에는 어떻게 적용해야 하는지 불분명하다는 문제가 있다. 그래서 이 논문에서는 규모가 매우 큰 모델에도 적용할 수 있는 방법에 집중하였고, 이를 위해 model scaling에 집중하였다.

Compound Model Scaling

1. Problem Formulation
2. Scaling Dimensions
3. Compund Scaling

1. Problem Formulation
   Convnet의 구조는 아래의 수식처럼 나타낼 수 있다.
   $N = F_{k} \odot...\odot F_{2} \odot F_{1}(X_{1}) = \bigodot_{j=1...k}F_{j}(X_{1})$
   $F_{i}$ 는 layer $i$ 에 대한 함수이고 이를 chain rule로 위와 같이 나타낼 수 있다.
   그리고 각 layer는 서로 다른 모양의 tensor를 input를 받기 때문에 이를 반영한 수식은 아래와 같다.
   $N = \bigodot_{i=1...s} F_i^{L_{i}}(X_{⟨H_{i},W_{i},C_{i}⟩})$
   model scaling을 할 때 각 층을 설계하면서 사용할 수 있는 자원에 대한 제약 조건을 만들어
   문제를 단순화하였다. 하지만 이러한 제약 조건에도 불구하고 $L_{i}, C_{i}, H_{i}, W_{i}$를 모두 탐색해야므로
   설계 규모는 여전히 큰 편이었다.
   그래서 설계 규모를 좀 더 줄이기 위해 모든 layer는 constant ration(상수비)로
   설계해야 한다는 제약 조건을 추가하였다.
   이러한 정해진 자원 속에서 model의 정확도를 최대화해야 한다는 이 논문의 목표는
   아래와 같은 수식 (Equation 2) 으로 나타낼 수 있다. ($\hat{F_{i}}, \hat{L_{i}}, \hat{H_{i}}, \hat{W_{i}}, \hat{C_{i}}$ 는 predefined parameter이다.)

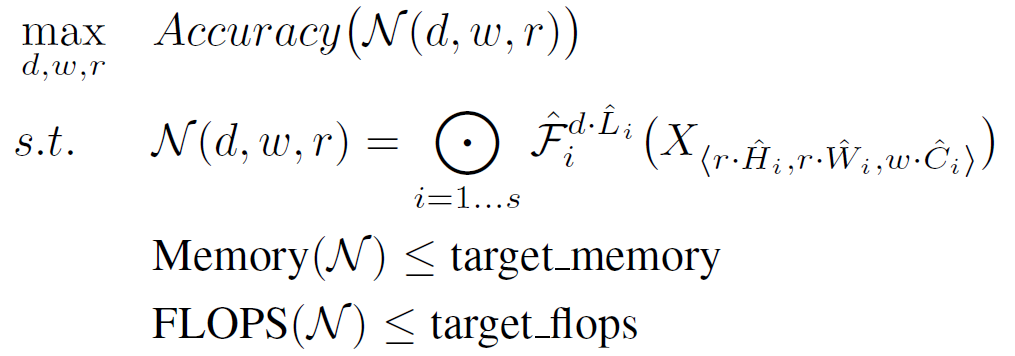
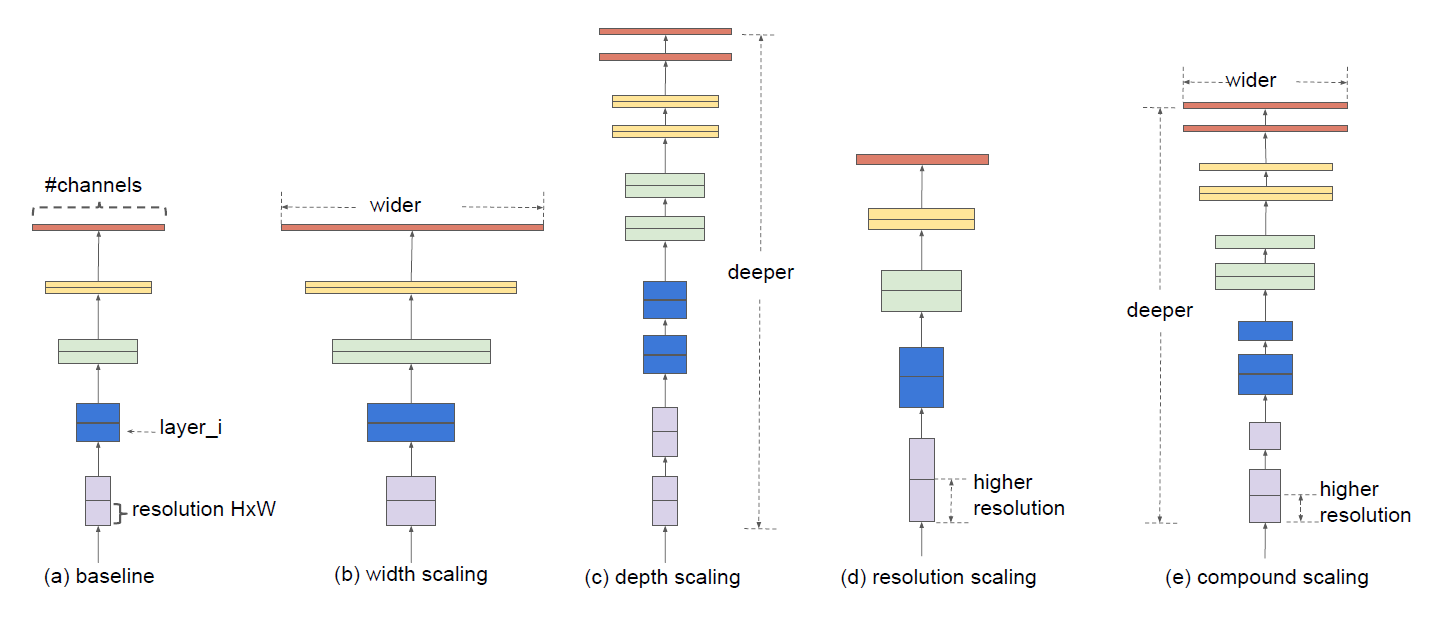
2. Scaling Dimensions (단일 dimension만 조절)

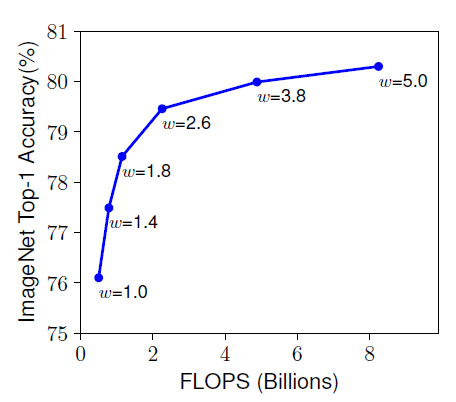
• Width ($w$)
  넓은 너비의 network는 feature를 더 잘 반영할 수 있고, 학습이 쉽다는 경향이 있다.
  하지만 너비만 넓은 network는 고차원 feature를 추출하기에는 어려움이 있다.
  그 결과 아래 그래프에서 보이는 것처럼 $w$ (너비)가 넓어질수록
  network가 빠르게 포화(saturate) 상태에 도달하게 된다.

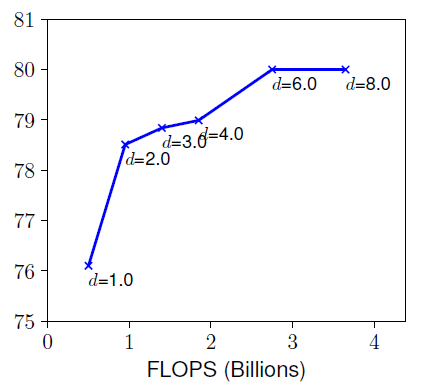
• Depth ($d$)
  network의 깊이가 깊어질수록 richer and complex feature를 얻을 수 있지만,
  아래 그래프처럼 깊이가 일정 수준에 도달하면 $d$ (깊이)가 커진다고 정확도의 차이는 없어진다.

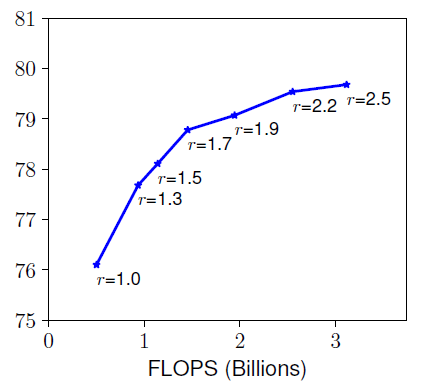
• Resolution ($r$)
  고화질의 input image는 fine-grained pattern을 추출하는 데 도움을 줄 수 있다.
  그래서 더 높은 정확도를 얻기 위해 고화질의 input image를 사용하기도 한다.
  하지만 아래 그래프에서 보이듯이 $r$ (화질)이 높아질수록 증가폭이 감소하는 것을
  확인할 수 있다.

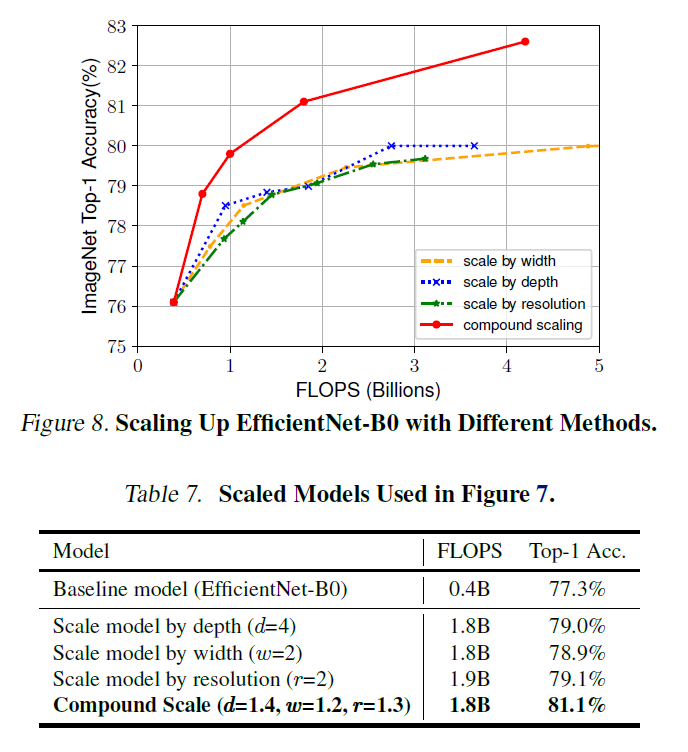
3. Compund Scaling
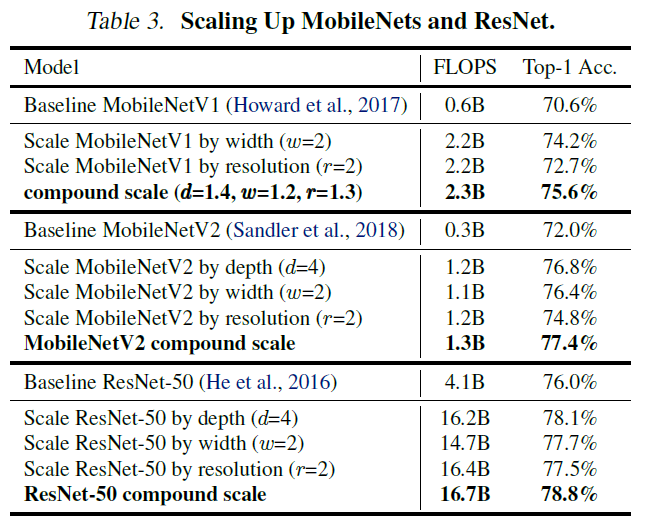
   위의 실험 결과를 보면 고화질 이미지가 처리하기 위해서는 고화질 이미지의 특징을 추출하기 위해 너비가 넓어야 하고, 추출된 풍부하고 복잡한 feature를 처리하기 위해 더 깊은 network가 필요하다는 것을 알 수 있다. 따라서 더 성능이 좋은 network를 만들기 위해서는 single dimension으로 scaling을 하는 것이 아닌 균형잡힌 compound scaling이 필요하다.
   그래서 이 논문에서는 아래 그래프처럼 여러 dimension을 조절하여 실험을 진행하였고, 그래프에서 보이는 것처럼 dimension을 하나만 조절하는 것보다 $d와r$을 모두 조절한 두 경우가 성능이 더 좋다는 것을 실험적으로 증명하였다.

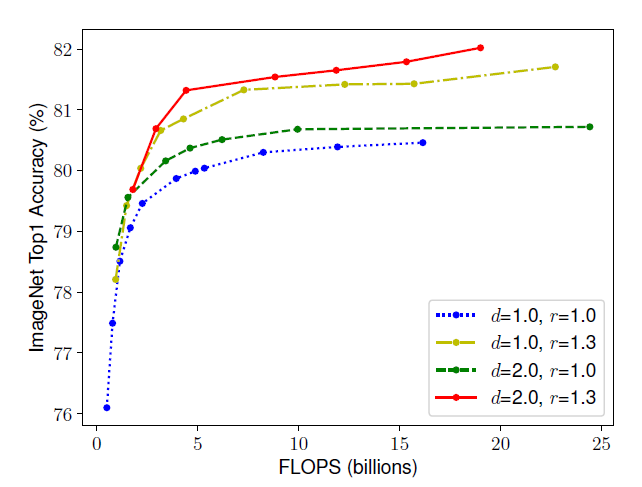
이처럼 network의 balance를 조절하는 연구는 이전에도 있었지만, 까다로운 tuning manual를 따라야 했다.
하지만 이 논문에서는 아래와 같은 새로운 compound scaling method를 제시하였다. (Equation 3)

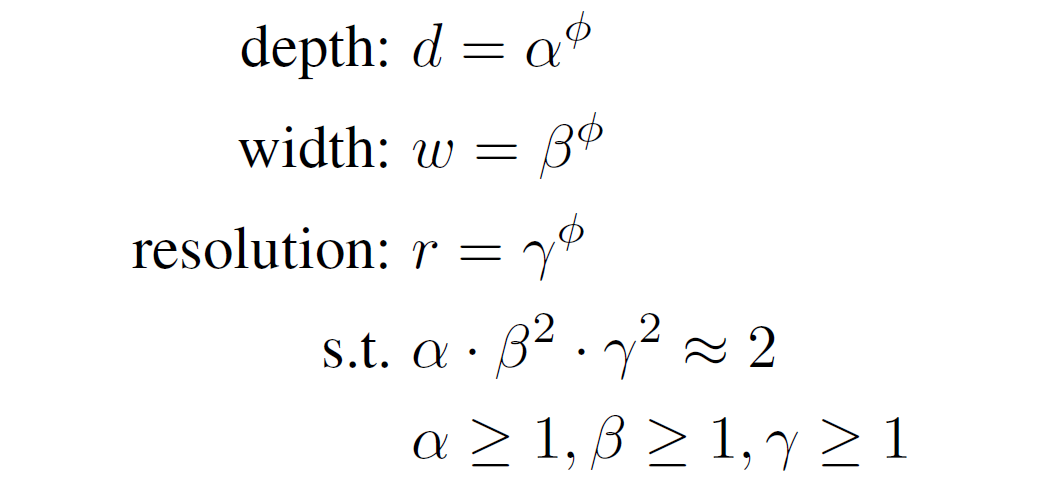
EfficientNet Architecture

model scaling은 layer operator를 바꾸지 않기 때문에 basline network의 중요도가 높다. 따라서 이 논문에서는 더 좋은 성능을 위해 새로운 baseline인 efficientNet을 만들었고 아래 table1이 EfficientNet-B0의 구조이다.

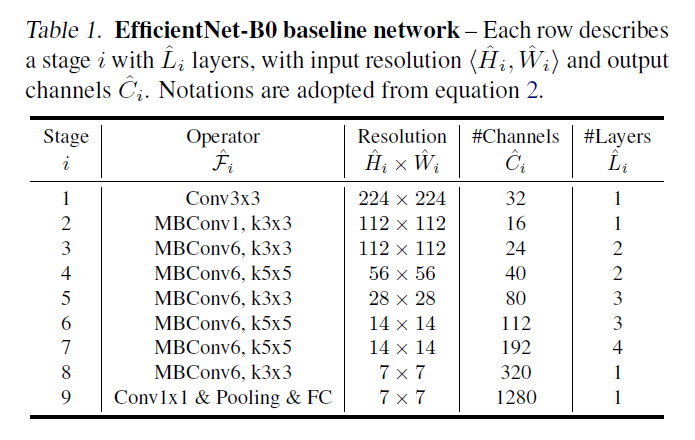
이 network에 적합한 compound scaling을 위해 equation2,3의 공식을 이용하여 $\alpha, \beta, \gamma$는 1.2, 1.1, 1.15이다.
그리고 EfficientNet-B0의 결과를 이용하여 EfficientNet-B1 ~ B7도 얻어냈다.

Experiments

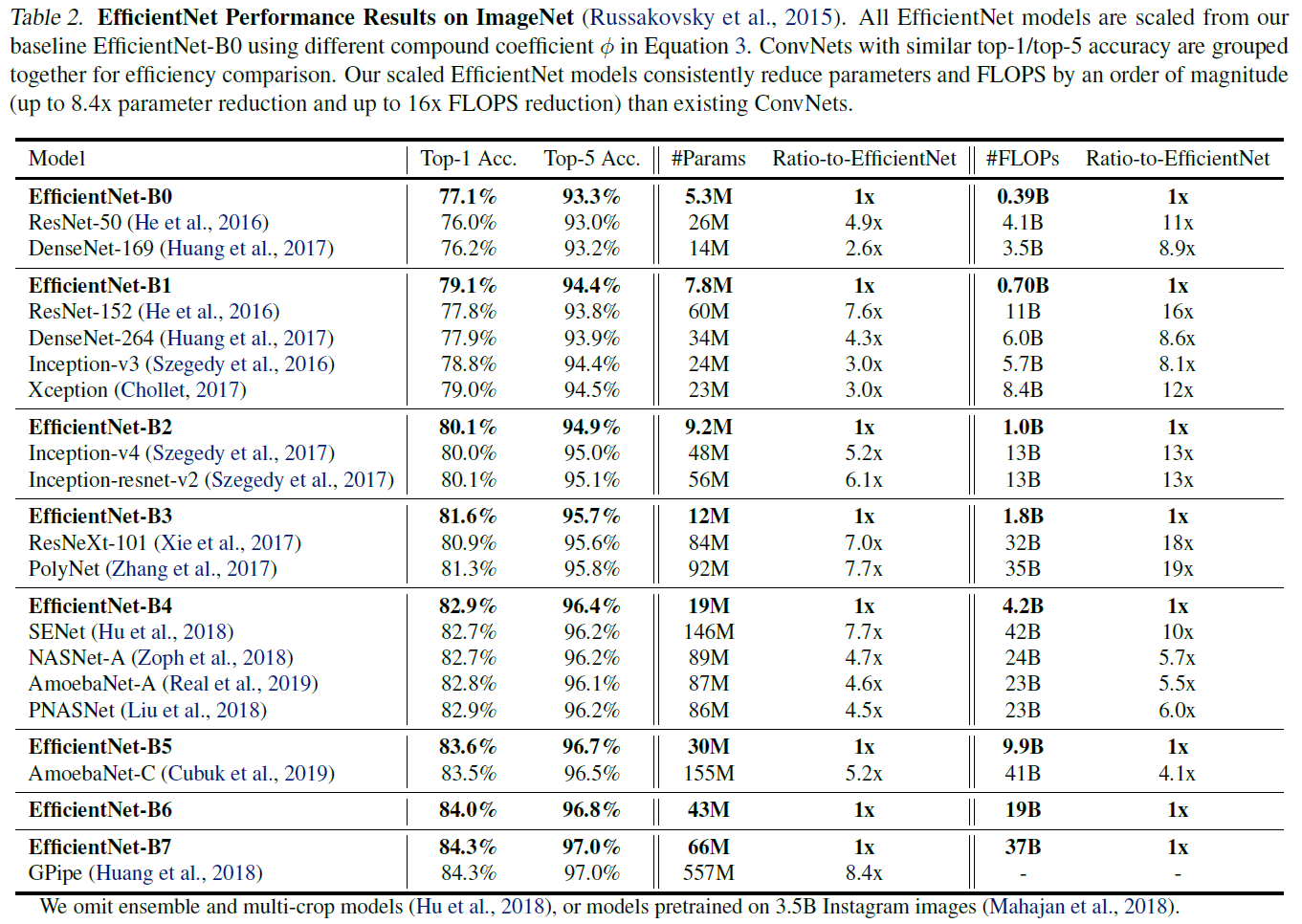
아래의 내용은 ImageNet에서 EfficientNet과 기존 network의 성능을 비교한 것이다.
(표에 있는 자세한 설명을 참고)