에라토스테네스의 체

핵심

• n 이하의 숫자에서 소수를 판별하기 위해:
  -가장 작은 소수 2부터 시작하여 해당 숫자의 배수(소수가 아님)를 모두 제거, 이후 남아 있는 숫자를 소수로 간주하고 그 배수를 제거하는 과정을 n의 제곱근까지 진행.
  -n의 제곱근까지 범위를 정하는 이유는 이 숫자에 도달하기까지 마주하는 모든 숫자는 2, 3, 5, 7, 11 등 특정 소수의 배수가 되므로 거를 수 있기 때문.
• 기본적인 용도는 소수의 판별.

쓰임

-소수 판별 및 생성
-약수 개수 또는 약수 합 계산
-소인수 분해 (가장 작은 소인수 활용)
-특정 범위에서의 소수의 합 계산
-골드바흐의 추측(짝수를 두 소수의 합으로 표현)
-어떤 수가 합성수인지 판별
-오일러 피 함수(Euler’s Totient Function) 계산

쓰임새

약수 판별

각 숫자 i가 자신의 배수들에게만 영향을 미친다는 점을 이용해 약수 계산 가능

약수의 성질

1. 숫자 n은 반드시 n의 배수의 약수.
   -n의 약수는 n의 배수의 약수가 됨.
2. 약수는 대칭적으로 존재.
   -작은 숫자부터 시작하여 해당 숫자의 배수를 처리하는 방식을 응용.

코드 구현

배수 관계 이용 : i는 반드시 i의 배수의 약수가 됨.
중복 계산 방지 : i의 배수만 처리하므로 효율적.
누적 계산 : 각 배수에 약수 개수를 누적.

function calculateDivisors(n) {
  // 배열 인덱스와 숫자를 1:1 대응시키기 위해 n+1로 배열 생성
    const divisors = Array(n + 1).fill(0);
    for (let i = 1; i <= n; i++) {
      // i의 배수(j+=i)에 대해 약수의 개수를 하나씩 증가
        for (let j = i; j <= n; j += i) {
            divisors[j]++;
        }
    }
    return divisors;
}
console.log(calculateDivisors(6)); // [0, 1, 2, 2, 3, 2, 4]

소수&합성수 판별

소수 및 합성수의 성질

소수 p의 배수는 모두 합성수임을 활용, 소수의 배수를 이용해 합성수를 빠르게 거르는 방식.

코드 구현

function sieve(n) {
    const isPrime = Array(n + 1).fill(true);
    isPrime[0] = isPrime[1] = false; // 0과 1은 소수가 아님
    for (let i = 2; i * i <= n; i++) {
        if (isPrime[i]) {
            for (let j = i * i; j <= n; j += i) {
                isPrime[j] = false; // i의 배수 제거
            }
        }
    }
    return isPrime;
}

const primes = sieve(10); // [false, false, true, true, false, true, false, true, false, false, false]
console.log(primes[7]); // true (7은 소수)

문제

• 에라토스테네스의 체를 응용, 합성수 구하기.
  

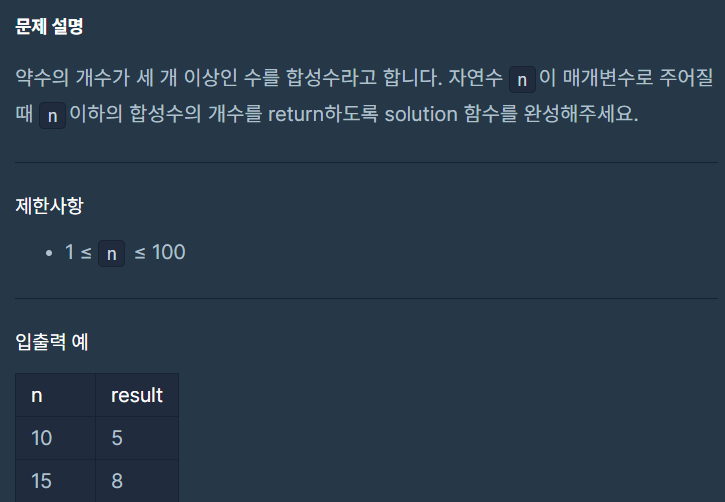
풀이

• 소수 여부를 판단하는 리스트를 만든 후, '소수 자신을 제외한 소수의 배수는 모두 합성수'임을 이용해 풀이.
  -[2,4,6,8] 에서 소수 2를 제외한 4, 6, 8은 모두 합성수. (n>2인 조건)

function solution(n) {
    // 소수 판별을 위한 배열을 생성하고 모든 값을 false로 초기화
    const isPrime = Array(n + 1).fill(false);
    let compositeCount = 0;

    for (let i = 2; i <= n; i++) {
        if (!isPrime[i]) {  // 소수라면
            for (let j = i * 2; j <= n; j += i) {
                isPrime[j] = true;  // i의 배수들은 합성수(true)로 표시
            }
        }
    }

    // 합성수의 개수 카운트
    for (let i = 2; i <= n; i++) {
        if (isPrime[i]) {
            compositeCount++;
        }
    }

    return compositeCount;
}

소인수 분해

i의 배수를 처리하면서 가장 작은 소인수를 기록, 소인수 분해를 빠르게 수행

소인수 분해의 성질

코드 구현

function smallestPrimeFactors(n) {
    const spf = Array(n + 1).fill(0); // spf[i]: i의 가장 작은 소인수
    for (let i = 2; i <= n; i++) {
        if (spf[i] === 0) { // 아직 처리되지 않은 경우
            for (let j = i; j <= n; j += i) {
                if (spf[j] === 0) spf[j] = i; // 가장 작은 소인수 기록
            }
        }
    }
    return spf;
}

console.log(smallestPrimeFactors(10)); // [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2]