이 파트에선 기초면서 자주 나오는 알고리즘 속 수학적 개념을 보겠다.
순열/조합, GCD와 LCM, 멱집합이 그 예다.
순열과 조합
예시는 과일로 들겠다.
순열
Permutation, 서로 다른 n개의 원소를 가지는 어떤 집합에서 중복 없이 순서에 상관있게 r개의 원소를 선택하거나 혹은 나열하는 것
예시
순열은 조합과 달리 순서도 따져서 부분집합을 만들기 때문에 경우의 수를 다 봐야한다.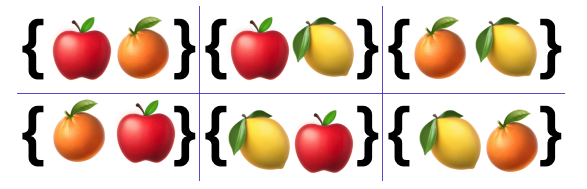
이므로 3P2 = 3! / (3-2)! = 6이 된다.
즉 공식은 이러하다. n은 원소의 총 개수를 의미하고, r은 그중 뽑는 개수를 의미한다.
조합
combination, 서로 다른 n개의 원소를 가지는 어떤 집합에서 중복 없이 순서에 상관없게 r개의 원소를 선택하는 것
예시
조합은 순서에 상관없이 원소를 선택해 부분집합을 만드는 걸로 경우의 수를 따져야한다.
순서에 상관 없이 3개 중 2개를 뽑아야하기에 3C2 = 3! / 2!(3-2)! = 3이다.
공식은 이러하다.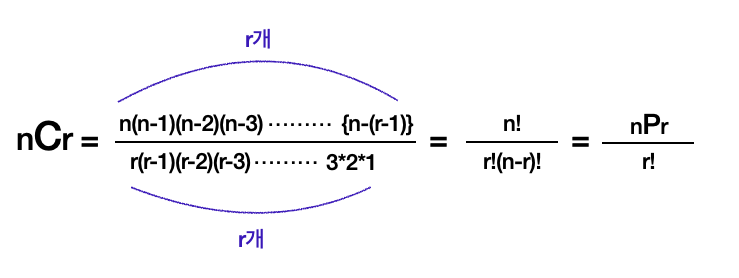
여기서 포인트는 중복을 허용하지 않기에 반드시 R ≤ N을 만족해야 한다는 것이다.
예제
문제: 카드 뽑기
[A, B, C, D, E]로 이뤄진 5장의 카드가 있습니다. 이 5장의 카드 중 3장을 선택하여 나열하려고 합니다. 이때, 다음의 조건을 각각 만족하는 경우를 찾아야 합니다.
- 순서를 생각하며 3장을 선택합니다.
- 순서를 생각하지 않고 3장을 선택합니다.
각 조건을 만족시키며 카드를 나열하는 방법은 각각 몇 가지일까요?
1번
- 모든 카드를 1장씩 나열하면서, 나열된 카드가 3장에 도달하면 카드의 나열을 중지
- 경우의 수를 구하기
- 첫번째 나열하는 카드를 선택하는 방법에는 다섯 가지가 있다.
- 첫번째 카드를 나열하고 난 다음, 두번째 카드를 선택하는 방법에는 네 가지가 있다.
- 두번째 카드를 나열하고 난 다음, 세번째 카드를 선택하는 방법에는 세 가지가 있다.
- 5 X 4 X 3 = 60 가지의 방법
즉, 순열의 방법으로 세웠고, 5P3 = 5! / (5-3)! = 5 4 3 = 60가지이다. 이를 바탕으로 코드를 세워보자
function permutationLoop() {
// 순열 요소가 인자로 주어질 경우, 인자 그대로 사용하면 되지만, 인자가 주어지지 않고
// 문제 안에 포함되어 있을 경우 이런 식으로 직접 적어서 사용
let lookup = ['A', 'B', 'C', 'D', 'E'];
let result = [];
// AAA부터 EEE까지 전부 만드는 코드에 검사 코드를 넣어 순열 완성
for (let i = 0; i < lookup.length; i++) {
for (let j = 0; j < lookup.length; j++) {
for (let k = 0; k < lookup.length; k++) {
// 동일한 인덱스인지 검사하고, 동일하다면 삽입하지 않고 다음으로 넘어감
if(i === j || j === k || k === i) continue;
result.push([lookup[i], lookup[j], lookup[k]])
}
}
}
return result;
}
permutationLoop();기본적인 반복문으로 풀었고, 반복문의 개수 === 요소를 뽑는 개수와 중복된 요소는 제거를 중첩하여 순열을 만들어 냈다.
결과 확인!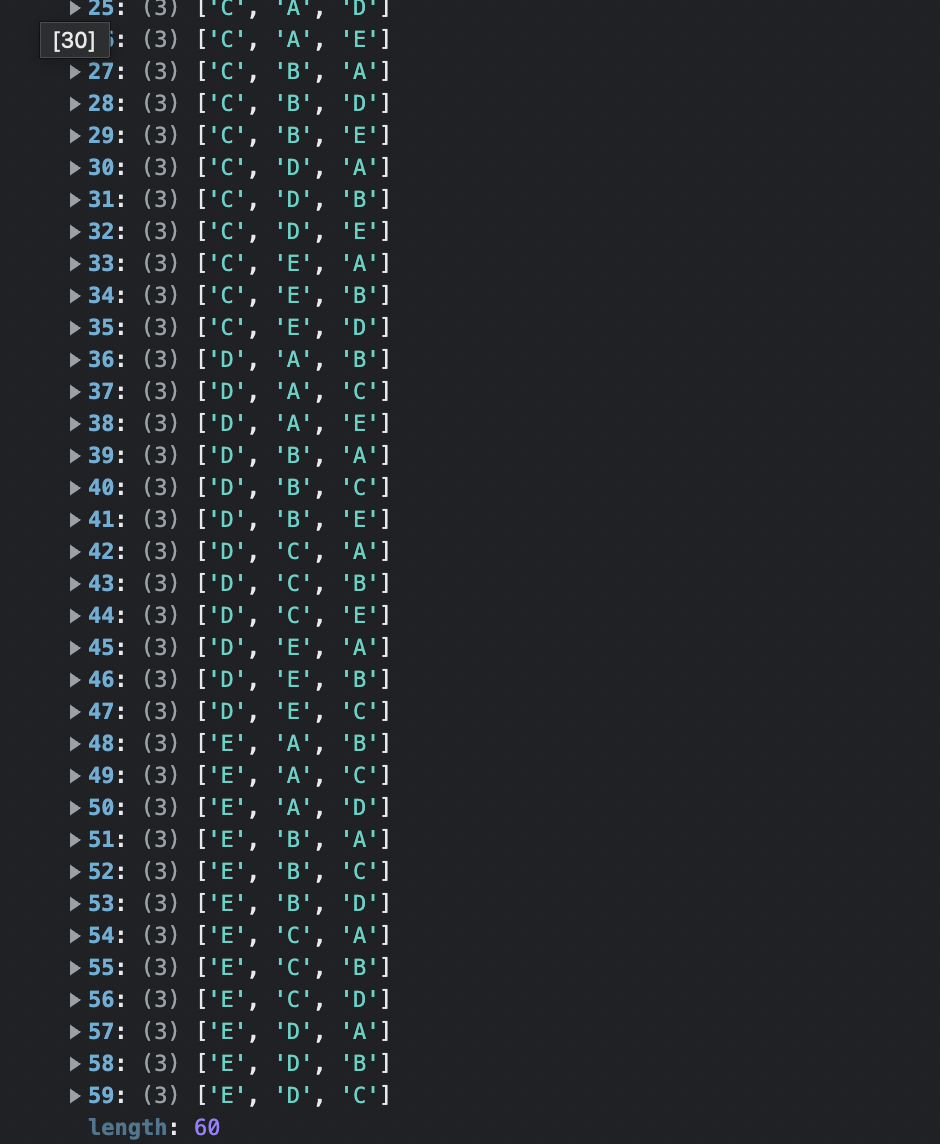
2번
1번과 비슷하게 3장을 하나의 그룹으로 선택하고 중복이 생기면 안되기에 각각 +1을 해서 중복을 최대한 피해봤다.
function combinationLoop() {
let lookup = ['A', 'B', 'C', 'D', 'E'];
let result = [];
console.log(lookup);
// 한 번 조합한 요소는 다시 조합하지 않는 조합의 특성상, i = 0, j = i + 1, k = j + 1의 조건을 달았음
for (let i = 0; i < lookup.length; i++) {
for (let j = i + 1; j < lookup.length; j++) {
for (let k = j + 1; k < lookup.length; k++) {
result.push([lookup[i], lookup[j], lookup[k]]);
}
}
}
return result;
}
combinationLoop();같은 순열과 제일 다른 건 i = 0, j = i + 1, k = j + 1인 부분이다.
지금까지 반복문으로만 조합과 순열을 만들었지만 개수가 늘어나면 반복문의 수도 늘어나고, 뽑아야 되는 개수가 n개처럼 변수로 들어왔을 때 대응이 어렵다. 다음엔 코테에 나올만한 주제로 재귀로 만든 코드로 작성해보자.
소수 찾기
한 자리 숫자가 적힌 종잇조각이 흩어져 있습니다. 흩어진 종잇조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다. 종이에 기록된 모든 숫자가 배열로 주어진다면, 이 종잇조각으로 만들 수 있는 소수는 몇 개인가요?
이 문제에는 순열이 숨어 있습니다. 만약 이 사실을 알아차린다면, 문제를 보다 쉽게 해결할 수 있습니다. 순열을 이용한다면, 다음과 같이 전략을 세울 수 있습니다.
- n 개의 숫자 중에 1~k 개를 뽑아서 순열을 생성합니다.
- 각 순열을 정수로 변환하고, 해당 정수가 중복되지 않으면서 동시에 소수인지 검사합니다.
- 소수라면 개수를 셉니다.
숫자는 순서에 의해 전혀 다른 값이 될 수 있습니다. 예를 들어 123과 321은 전혀 다른 숫자입니다. 만약 이 문제를 조합으로 접근하게 된다면, 123과 321은 같은 경우로 취급합니다. 따라서, 순서를 고려하지 않고 k 개를 뽑아내는 조합으로는 이 문제를 해결할 수 없습니다.
코드를 입력하세요문제: 일곱 난쟁이
왕비를 피해 일곱 난쟁이와 함께 평화롭게 생활하고 있던 백설 공주에게 위기가 찾아왔습니다. 하루일과를 마치고 돌아온 "일곱" 난쟁이가 "아홉" 명이었던 겁니다. 아홉 명의 난쟁이는 모두 자신이 "백설 공주와 일곱 난쟁이"의 주인공이라고 주장했습니다. (뛰어난 수학적 직관력을 가지고 있던) 백설 공주는 일곱 난쟁이의 키의 합이 100임을 기억해 냈습니다. 아홉 난쟁이 각각의 키가 주어질 때, 원래 백설 공주와 평화롭게 생활하던 일곱 난쟁이를 찾는 방법은 무엇인가요?
위 문제는 조합을 이용해서 일곱 난쟁이를 찾을 수 있습니다. 모든 일곱 난쟁이의 키를 합했을 때 100이 된다고 주어졌기 때문에, 9명의 난쟁이 중 7명의 난쟁이를 순서를 생각하지 않고, 난쟁이 7명의 키를 합했을 때 100이 되는 경우를 찾으면 됩니다.
코드를 입력하세요GCD/LCM
최대공약수와 최소공배수의 규칙을 알아보자
GCD
최대공약수, 두 수 이상의 여러 공약수 중 최대인 수
먼저 공약수의 개념을 알아보면 약수 중 공통된 부분을 뜻한다.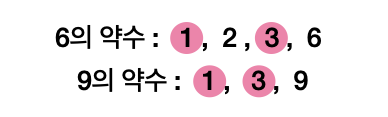
여기 위 사진을 보고 6과 9의 최대공약수는 3이라 결론내릴 수 있다.
LCM
최소공배수, 두 수 이상의 여러 공배수 중 최소인 수
공배수는 두 수 이상의 여러 수 중 공통된 배수(하나의 수에 정수를 곱한 수)를 의미, 다시 말해 그 수에 의해 나누어 떨어지는 수인 배수를 뜻한다.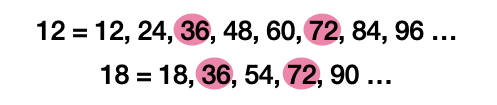
위 사진을 보고 해당 수의 배수를 나열해 겹쳐지는 수를 찾으면 36, 72, 108, ... 이고, 최소공배수는 제일 작은 36이다.
공식: 유클리드 호제법
개념보다 중요한 공배수 공약수를 구분짓는 공식이 있다.
유클리드 호제법은 최대공약수와 최소공배수를 구하는 모든 문제에 일단 적용해보고 시작할 수 있게 할 수 있을 정도로 굳혀진 공식이다.
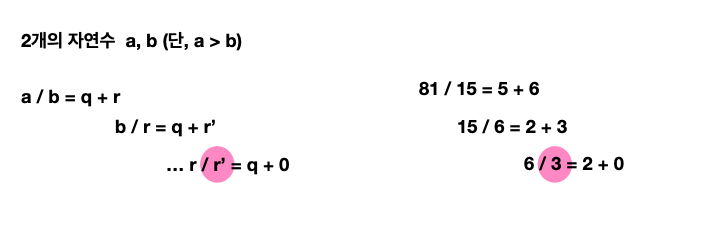
q는 몫(Quotient)을 의미하고, r은 나머지(Rest)를 의미한다.
2개의 자연수 a와 b가 있을 때, a가 b보다 커야 한다는 조건(절대적 조건)하에 a를 b로 나눈 나머지를 r이라 하면 a와 b의 최대공약수는 b와 r의 최대공약수와 같다는 이론
이러한 개념에 따라 b를 r로 나눈 나머지 r’를 구하고, 다시 r을 r’로 나누는 과정을 반복해, 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수임을 알 수 있게 된다.
여기 81과 15가 있다. 같은 방식으로 쭉 나눴을 때, 마지막 나눗셈에서 나누는 수인 3이 최대공약수임을 확인할 수 있다.
알고리즘 공식으로 구현했을 때 로직은 이렇다.
function gcd(a, b){
while(b !== 0){
let r = a % b;
a = b;
b = r;
}
return a;
}나눈 뒤 재할당을 계속 한다. while문으로 이루어진 중심 로직이 있고, 모든 자연수를 0으로 나누게 되면 리턴되는 값이 Infinity이기 때문에 버그 방지 및 공식 구현으로 b가 0이 되는 순간 반복을 끝나게 만들었다.
최소공배수를 구하는 법
사실 간단하다.
a * b = 최대공약수(GCD) * 최소공배수(LCM)
GCD/LCM 특성을 이용한 공식 중 위의 공식이 있는데 저기서 유클리드 호제법으로 구한 GCD를 두 수를 곱한 곳에 나눈다면? LCM이 나올 것이다. 간단!
function lcm(a, b){
return a * (b / gcd(a, b));
}위 유클리드 호제법을 이용해 최대공약수를 구하고, 그걸 나눠주는 모습이다. 결과는?!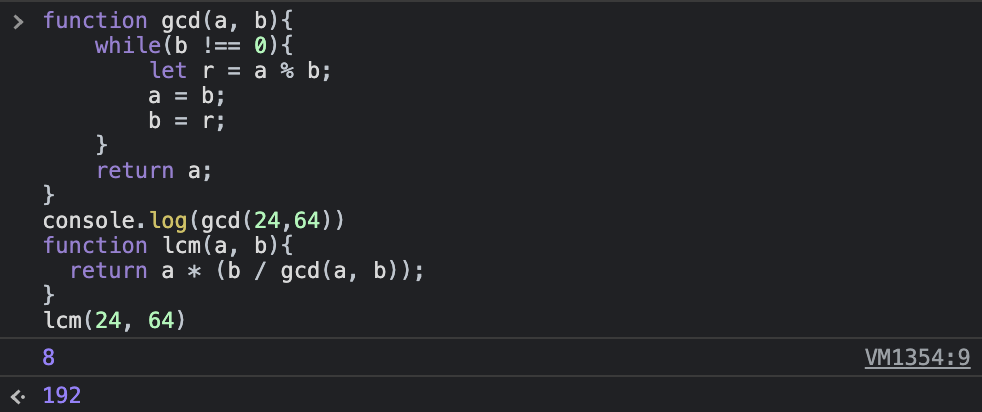
예제
멱집합
어떤 집합이 있을 때, 이 집합의 모든 부분집합
예를 들어, 집합 {1, 2, 3}의 모든 부분집합은 {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} 으로 나열할 수 있고, 이 부분집합의 총 개수는 8개다. 이 모든 부분집합을 '멱집합'이라고 한다.
알고리즘에선 자기 자신을 호출하며 문제를 더 작은 문제로 문제의 크기를 줄여 해결하는 방식으로 많이 사용한다. 문제가 가장 작은 단위로 줄어들고, 함수가 리턴될 때 카운트를 올리는 방식으로 멱집합의 개수를 구할 수 있다.
과정
멱집합을 구하는 과정은 여러가지 방법이 있는데, 부분집합을 나열하는 방법에서 가장 앞 원소(혹은 임의의 집합 원소)가 있는지, 없는지에 따라 단계를 나누는 기준을 결정하는 단계로 나눠보자
- Step A: 1을 제외한 {2, 3}의 부분집합을 나열합니다.
- Step B: 2를 제외한 {3}의 부분집합을 나열합니다.
- Step C: 3을 제외한 {}의 부분집합을 나열합니다. → {}
- Step C: {}의 모든 부분집합에 {3}을 추가한 집합들을 나열합니다. → {3}
- Step B: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열합니다.
- Step C: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열하려면, {}의 모든 부분집합에 {2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {2, 3}을 추가한 집합들을 나열합니다. → {2}, {2, 3}
- Step B: 2를 제외한 {3}의 부분집합을 나열합니다.
- Step A: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열합니다.
- Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면, {3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열합니다.
- Step C: {3}의 모든 부분집합에 {1}을 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 3}을 추가한 집합들을 나열합니다. → {1}, {1, 3}
- Step C: {3}의 모든 부분집합에 {1, 2}를 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 2, 3}을 추가한 집합들을 나열합니다. → {1, 2}, {1, 2, 3}
- Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면, {3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열합니다.
되게 복잡해보이지만 트리 구조와 비슷한 모식도를 가진다.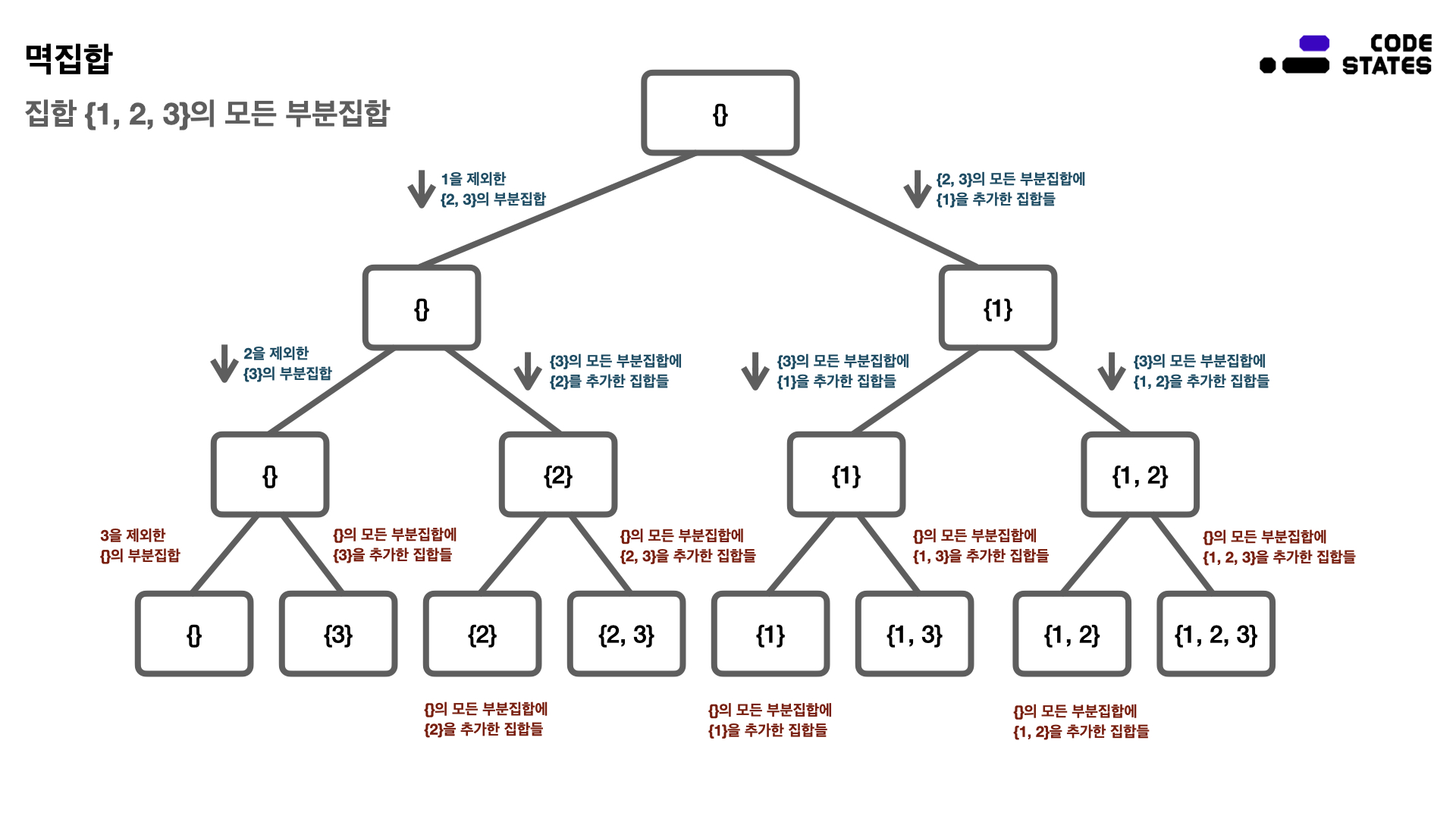
그렇다고 트리 구조 문제는 아니다~ 그저 순환 구조를 띠는 것을 확인할 수 있는 수단으로 보여주는 것이다.