버블 정렬, 삽입 정렬 등 다양한 정렬 알고리즘을 학습하던 중, 문득 이런 의문이 들었습니다. 정렬 문제를 풀 때 항상 사용하는 sort() 메서드가 어떤 원리로 작동할까요? 시간복잡도가 O(n log n)이라는 것은 알았지만, 어떤 정렬 알고리즘을 쓰는지 궁금했습니다.

그래서 이번에는 JS sort() 메서드의 내부 동작 원리에 대해 파헤쳐보려고 합니다.

정렬 알고리즘 종류 / 배경 지식

다양한 정렬 알고리즘 비교

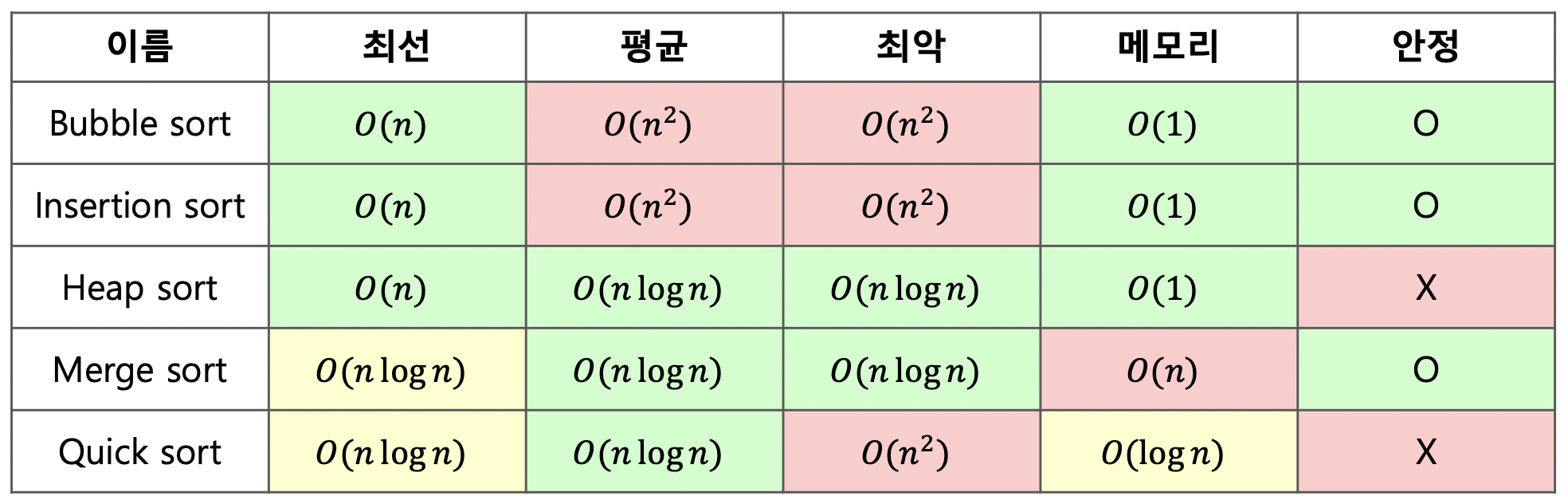
위 이미지는 버블, 삽입(Insertion), 힙, 병합(Merge) 등 다양한 정렬 알고리즘의 시간복잡도, 메모리 사용량, 안정성(Stability)을 보여주는 표입니다.

여기서 가장 중요한 건 시간복잡도입니다. 배열의 크기와 초기 정렬 상태에 따라 최선, 평균, 최악의 경우로 나누어 시간복잡도를 표시했습니다.

시간복잡도 이해

시간복잡도란 n개의 배열이 입력값으로 있을 때 정렬에 걸리는 시간을 '빅오 표기법'으로 나타낸 것입니다. 일종의 상대적인 측정 단위라고 생각하시면 됩니다.

• O(1): 입력 크기와 상관없이 항상 일정한 시간이 걸림
• O(n): 입력 크기에 비례해 선형적으로 시간이 증가
• O(log n): 입력이 커져도 시간이 매우 완만하게 증가 (이진 탐색 등)
• O(n log n): 많은 효율적인 정렬 알고리즘이 이 정도 속도
• O(n²): 버블 정렬처럼 이중 루프를 사용하는 알고리즘의 복잡도

실용적인 정렬 알고리즘을 만들려면 최소한 O(n log n) 이하의 시간복잡도를 가져야 합니다.

참조 지역성 원리

시간복잡도 공식은 C × n log n + α 형태로 볼 수 있는데, 여기서 C는 '참조 지역성 원리'에서 나오는 상수로, 실제 실행 시간에 큰 영향을 미칩니다.

참조 지역성 원리란?
마치 책상 위에 자주 쓰는 물건을 가까이 두는 것처럼, CPU도 최근에 사용한 데이터를 캐시에 저장해 빠르게 접근

쉽게 말해 CPU는 메모리에서 데이터를 읽을 때,

1. 연속된 메모리 위치를 읽는 것이 더 빠름
2. 최근 참조한 메모리를 다시 참조할 확률이 높음

이런 이유로 같은 O(n log n) 시간복잡도를 가진 정렬 알고리즘이라도 실제 성능은 크게 차이날 수 있습니다.

예를 들어, 힙 정렬은 같은 O(n log n) 알고리즘이지만 메모리를 건너뛰며 접근하는 특성 때문에 캐시 친화적이지 않아 실제로는 더 느립니다.

완벽한 정렬 알고리즘은 있을까?

개발자들은 효율적인 정렬 메서드가 필요했습니다. 매번 정렬 알고리즘을 작성하는 것은 비효율적이어서, 통용되는 정렬 방식으로 메서드를 만드려고 했습니다.

그런데 문제는 모든 상황에 최적인 단일 정렬 알고리즘이 없다는 것이었습니다.

• 퀵 정렬: 피벗을 기준으로 작은 값과 큰 값을 분할해 정렬. 평균 O(n log n)으로 빠르지만, 정렬된 배열에서 최악의 경우 O(n²)
• 병합 정렬: 배열을 반으로 나눠 각각 정렬한 후 병합. 항상 O(n log n) 보장하지만 배열 크기만큼 추가 메모리 필요
• 힙 정렬: 힙 자료구조를 사용해 정렬. 항상 O(n log n) 보장하고 추가 메모리도 적지만, 메모리 접근 패턴이 불규칙해 캐시 효율이 낮아 실제로는 느림

이런 상황에서 Tim Peters라는 개발자가 등장했습니다. 그는 2002년 파이썬을 위해 새로운 하이브리드 정렬 알고리즘인 'Tim sort'를 개발했습니다.

Tim Sort의 등장

이 알고리즘은 삽입 정렬과 병합 정렬의 장점을 결합해 실생활 데이터에 최적화된 정렬을 제공합니다.

• 최선의 경우: O(n) (이미 정렬된 데이터)
• 평균 및 최악의 경우: O(n log n)

현재 이 알고리즘은 Python, Java, JS, Android, Swift 등 다양한 프로그래밍 언어에서 표준 정렬 알고리즘으로 채택됐습니다.

Tim Sort 핵심 아이디어

Tim sort의 가장 중요한 아이디어는 작은 부분에는 삽입 정렬, 큰 부분에는 병합 정렬을 적용하는 것입니다.

• 이미 정렬된 구간(Run)을 찾아서 빠르게 정렬
• 짧은 구간은 삽입 정렬(Insertion Sort) 사용 → 빠르고 캐시 친화적
• 긴 구간은 병합 정렬(Merge Sort) 방식으로 안정적으로 정렬

[!TIP]

Tim Sort 과정을 그린 유튜브 영상을 보면 더욱 이해가 잘 됩니다!

Run: Tim Sort의 독특한 개념

Tim sort는 배열을 일정 크기의 덩어리(Run)로 나눕니다. 각 Run은 두 가지 방식으로 생성됩니다.

1. 증가하는 Run: a₀ ≤ a₁ ≤ a₂ ≤ a₃ ≤ ...
2. 감소하는 Run: a₀ > a₁ > a₂ > a₃ > ...

배열을 순회하면서 이런 패턴을 감지해 Run을 형성하고, 감소하는 Run은 뒤집어서 모두 증가하는 Run으로 만듭니다. 실생활 데이터는 무작위가 아닌 경우가 많아 이미 정렬된 부분이 많기 때문에 효율적입니다.

각 Run이 최소 크기(minrun)보다 작으면 이진 삽입 정렬을 사용해 확장합니다. 이 minrun 값은 전체 배열 크기에 따라 조정되며, 일반적으로 32~64 사이의 값을 가집니다.

작동 과정: Timsort 알고리즘의 실제 흐름

1. Run 탐색: 이미 정렬된 구간 찾기

Timsort는 먼저 배열을 훑어보면서 이미 정렬된 부분(Run)들을 찾아냅니다. 마치 책상 위 서류더미에서 이미 정리된 묶음을 발견하는 것과 같습니다.

예시 배열: [8, 9, 10, 6, 3, 1, 2, 4, 11, 12]

# Run 찾기
  - [8, 9, 10] ← 첫 번째 Run (이미 오름차순)
  - [6] ← 두 번째 Run (한 개짜리 Run)
  - [3] ← 세 번째 Run (한 개짜리 Run)
  - [1, 2, 4] ← 네 번째 Run (이미 오름차순)
  - [11, 12] ← 다섯 번째 Run (이미 오름차순)

이때 내림차순으로 정렬된 부분을 발견하면 즉시 뒤집어서 오름차순으로 만듭니다.

만약 [5, 4, 3]이란 내림차순 부분이 있다면
		↓ 뒤집기!
[3, 4, 5]로 변환 (오름차순 Run)

현실의 데이터는 대부분 완전히 무작위가 아니라 어느 정도 패턴이 있습니다.

• 날짜순으로 기록된 로그 파일
• 이미 부분적으로 정렬된 고객 목록
• ID 순서대로 저장된 사용자 데이터

Timsort는 이런 특성을 활용해 범용성과 속도를 높였습니다.

2. Run 보강: 작은 Run은 삽입 정렬로 확장

발견한 Run이 너무 짧으면(보통 32개 미만), 이진 삽입 정렬로 확장합니다.

일반 삽입 정렬은 삽입 위치를 찾기 위해 모든 요소와 비교하지만, 이진 삽입 정렬은 이진 탐색으로 삽입 위치를 찾아 비교 횟수를 O(log n)으로 줄입니다.

minrun = 4라고 가정 (실제로는 배열 크기에 따라 달라짐)

# Run 보강 과정
  - [8, 9, 10] → 이미 3개라 거의 minrun 크기
  - [6] → 너무 작음! → [3, 6]로 확장 (이진 삽입 정렬 사용)
    - 6 유지
    - 3을 어디에 넣을지 이진 탐색 → 6 앞에 삽입
    - 결과: [3, 6]
  - 이런 식으로 계속 진행...

이진 삽입 정렬은 아래처럼 작동합니다.

1. 현재 검사 중인 요소를 임시 저장
2. 이미 정렬된 부분에서 '이진 탐색'으로 삽입 위치 찾기
3. 필요하면 요소들을 오른쪽으로 밀고 찾은 위치에 삽입

앞서 설명한 것처럼, 작은 범위에서는 삽입 정렬이 매우 효율적입니다.

[!TIP]

왜 짧은 구간엔 삽입 정렬을 사용할까요?
일반적으로 삽입 정렬은 O(n²)로 느리지만, 작은 데이터셋에서는 오버헤드가 적고 이미 부분적으로 정렬된 데이터에서 효율적이기 때문입니다. 게다가 참조 지역성이 매우 좋아서 캐시 효율성이 높습니다.

3. 병합 과정: Run들을 퍼즐처럼 맞춰가기

정렬된 Run들을 쌓아가며 병합합니다. 이때 Run들의 상대적 크기를 고려해 병합 순서를 결정합니다. Run들을 스택에 쌓으면서 아래와 같은 조건을 유지합니다.

• |X| > |Y| + |Z| (X, Y, Z는 스택 상단 3개의 Run)
• |Y| > |Z|

스택에 Run들을 쌓으면서
- 가장 위 세 개의 Run을 X, Y, Z라고 할 때 (Z가 맨 위)
- 만약 |X| ≤ |Y| + |Z| 또는 |Y| ≤ |Z| 조건이 맞으면
  • 더 작은 Run을 큰 Run과 병합

예시
- 스택: [Run1(길이 30), Run2(길이 20), Run3(길이 10)]
- |Run1| = 30, |Run2| = 20, |Run3| = 10
- 30 ≤ 20 + 10? → 맞음! → Run2와 Run3 병합
- 결과: [Run1(길이 30), 새Run(길이 30)]

이렇게 하면 비슷한 크기의 Run끼리 병합돼 성능과 효율성이 높아집니다!

추가 최적화: 갤로핑 기법

두 Run을 병합할 때 Timsort는 Galloping이라는 최적화 기법을 사용합니다.

두 Run [A, B, C, D]와 [E, F, G, H] 병합 시

1. 작은 Run 복사
   임시 버퍼에 더 작은 Run만 복사 (메모리 절약)

2. 최적 구간 찾기
   - A < E인지 확인? → 맞다면 A는 이미 제 위치
   - H < D인지 확인? → 맞다면 H는 이미 제 위치
   - 실제 비교가 필요한 구간만 병합

3. 갤로핑 기법
   - 연속해서 같은 Run에서 요소를 가져오게 되면
   - '이쪽 Run이 계속 이길 것 같은데?' 판단
   - 이진 탐색으로 여러 요소를 한꺼번에 가져옴
   
   예: A, B, C, D와 W, X, Y, Z 비교 시
   A < W, B < W, C < W... → 
   '아, A~K까지는 다 W보다 작겠구나!'
   → 한 번에 여러 요소 처리

갤로핑 기법은 Run이 커지면 커질 수록 더 빠르게 가져오도록 합니다. 요소 비교 횟수를 대폭 줄여 속도를 높이죠!

참고: JS로 구현한 갤로핑

function galloping(arr, key, start, end) {
  // 1, 3, 7, 15, ... 지수적으로 탐색 범위 증가
  let offset = 1;
  
  // 범위 확장 단계
  while (start + offset < end && arr[start + offset] < key) {
    offset = (offset * 2) + 1;
  }
  
  // 이진 탐색으로 정확한 위치 찾기
  const searchStart = start + Math.floor(offset / 2);
  const searchEnd = Math.min(start + offset, end);
  
  // 이진 탐색 수행
  return binarySearch(arr, key, searchStart, searchEnd);
}

전체 과정 한눈에 보기

1. 배열 훑기
   → 정렬된 Run 찾기
   → 내림차순은 뒤집기

2. Run 보강
   → 너무 작은 Run은 이진 삽입 정렬로 확장

3. Run 병합
   → 균형 맞추며 병합 (비슷한 크기끼리)
   → 갤로핑 기법으로 병합 속도 개선
   → 모든 Run이 하나로 합쳐질 때까지 반복

4. 정렬 완료!

Timsort는 이런 방식으로 이론적인 효율성과 실용적인 최적화를 모두 달성합니다.

결론

이 알고리즘은 무작위 데이터보다는 부분적으로 정렬되어 있거나 패턴이 있는 실제 데이터에서 최고의 성능을 발휘합니다.

시간복잡도 분석

Timsort의 시간복잡도가 O(n log n)인 이유는

1. Run 찾기: 배열 순회 O(n)
2. Run 보강: 이진 삽입 정렬 사용, 실질적으로 O(n)
   • minrun 상수(32~64)로 제한돼 O(k log k)가 결국 O(n)
3. Run 병합: 모든 요소가 최대 log n번 병합에 참여하므로 O(n log n)

즉, O(3n + n log n)이 걸리고, 점근적 분석으로 봤을 때 O(n log n)으로 귀결됩니다.

• 최선의 경우: O(n) - 이미 정렬된 데이터
• 평균/최악의 경우: O(n log n)

갤로핑(Galloping) 같은 최적화 기법도 있습니다. 최악의 경우 분석에는 영향을 주지 않지만, 실제 성능은 상당히 개선합니다. 특히 부분적으로 정렬된 데이터에서 요소 비교 횟수를 크게 줄여줍니다.

메모리 효율성: 병합 정렬과 비교

병합 정렬은 아래와 같습니다.

• 공간복잡도: O(n)
• 전체 배열 크기의 임시 메모리 필요

Timsort는 이를 더 효율적으로 만들었습니다.

• 공간복잡도: O(n)이지만 실제 더 적게 사용
• 최악의 경우도 n/2 정도의 메모리만 사용
• 주요 최적화
  1. 더 작은 Run만 임시 버퍼에 복사
  2. 자연적 Run 활용으로 초기 분할 메모리 절약
  3. 버퍼 크기 미리 계산해 한 번만 할당
  4. 갤로핑 기법으로 메모리 접근 감소

물론 Tim Sort도 단점도 있습니다.

1. 구현 복잡성: 다양한 최적화 기법을 포함하고 있어 구현이 복잡하고 디버깅이 어려움
   • 적어도 JS에서는 단점으로 안되겠네요!
2. 메모리 사용: 병합 정렬보다는 적지만, 그래도 메모리를 많이 씀 (최악의 경우 O(n/2) 임시 메모리 사용)
3. 완전 무작위 데이터에서의 성능: 실생활 데이터 패턴에 최적화되어 있어 완전히 무작위한 데이터에서는 다른 알고리즘보다 이점이 줄어듦
4. 오버헤드: 작은 배열에서는 다양한 최적화 로직으로 인한 오버헤드가 상대적으로 크게 작용할 수 있음
5. 시스템 의존성: 캐시 크기, 메모리 레이아웃 등 하드웨어 특성에 따라 성능 차이가 발생할 수 있음

---

하지만, Tim sort는 최악의 경우에도 O(n log n) 시간복잡도를 보장하면서, 범용적인 상황에서 실제 성능도 매우 뛰어납니다. 메모리 사용량도 병합 정렬보다 효율적으로 관리하고, 안정적인 정렬을 제공합니다.
그래서 다양한 프로그래밍 언어에서 채택된 것이죠.

이러한 장점으로 많은 언어에서 표준 정렬 알고리즘으로 채택해 사용하고 있습니다! 고마워요 팀!

참고 자료

• 알고리즘 이론: 정렬-sort()
  
• Tim sort에 대해 알아보자 - Naver D2
• 정렬 알고리즘의 시각화 - VisuAlgo