Preprocess
입지선정 모델
1. MCLP(Maximal Covering Location Problem)
시설물의 개수 혹은 예산 비용이 제한되었을 때, 시설물의 서비스 수준을 높이기 위하여
주어진 제약조건 하에서 시설물이 커버하는 수요량을 최대화하는 위치를 선정하는 방법
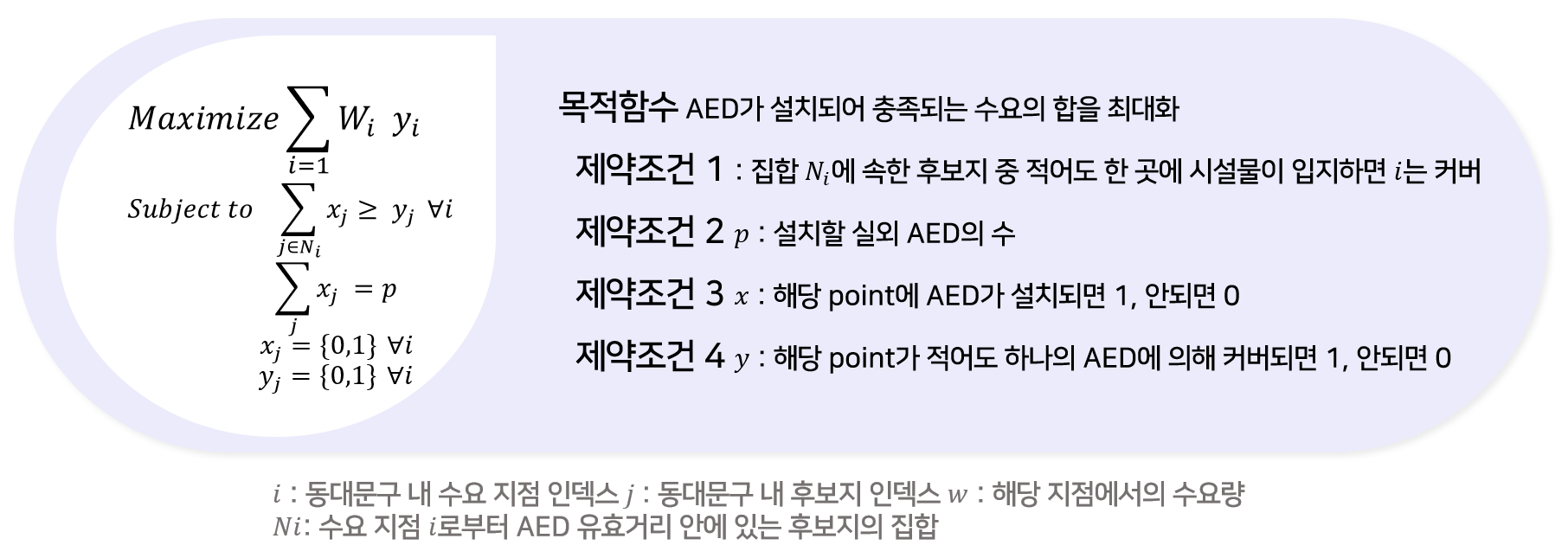
2. 가정 1: 수요지점 인덱스 i와 후보지 인덱스 j는 동일

3. 가정 2: AED의 유효거리는 200m

4. 가정 3: 도보 노드-링크 데이터를 활용한 후보지 선정
- 기존 AED는 대부분 아파트, 공공기관, 관리사무소와 같은 건물 내부에 위치한다.
- 24시간 커버되지 못하는 외부지역에 설치하기 위하여 도보 노드-링크 데이터에서 노드들을 후보지로 활용한다. (8,541개)
- 노드는 보행자들이 실제로 지나다니는 길들이 만나는 교차점을 의미한다.
df = pd.read_csv('./서울시 자치구별 도보 네트워크 공간정보.csv', encoding='cp949')
df = df[(df['노드링크 유형'] == 'NODE') &
(df['시군구명'] == '동대문구') &
(df['육교'] == 0) &
(df['횡단보도'] == 0)]
# 용두동 + 신설동 = 용신동
df.loc[(df['읍면동명'] == "용두동") |
(df['읍면동명'] == "신설동"), "읍면동명"] = "용신동"
df = df[['노드 WKT', '노드 ID', '시군구명', '읍면동명']].reset_index(drop=True)# geodata 변경 buffer 생성 - 기존 24시간 가동 AED와의 유효거리 기반 수요량 b(buffer_100)
gs = gpd.GeoSeries.from_wkt(df['노드 WKT'])
df_dobo_100 = gpd.GeoDataFrame(df, geometry = gs, crs = 'epsg:4326')
df_dobo_100 = df_dobo_100.set_geometry('geometry')
df_dobo_100['buffer_100'] = df_dobo_100.to_crs('epsg:5179').buffer(100).to_crs('epsg:4326')
df_dobo_100 = df_dobo_100.set_geometry('buffer_100')
df_dobo_100['buffer_100_coordinates'] = df_dobo_100['buffer_100'].apply(polygon_to_coordinates)
df_dobo_100['lon'] = df_dobo_100['geometry'].x
df_dobo_100['lat'] = df_dobo_100['geometry'].y
df_dobo_100 = pd.merge(df_dobo_100, pop[['행정동코드명', 'a']], how= 'left', right_on = '행정동코드명', left_on = '읍면동명')
del df_dobo_100['행정동코드명'], df_dobo_100['노드 WKT']
# geodata 변경 buffer 생성 - 알고리즘 제약조건 및 시각화(buffer_200)
gs = gpd.GeoSeries.from_wkt(df['노드 WKT'])
df_dobo_200 = gpd.GeoDataFrame(df, geometry = gs, crs = 'epsg:4326')
df_dobo_200 = df_dobo_200.set_geometry('geometry')
df_dobo_200['buffer_200'] = df_dobo_200.to_crs('epsg:5179').buffer(200).to_crs('epsg:4326')
df_dobo_200 = df_dobo_200.set_geometry('buffer_200')
df_dobo_200['buffer_200_coordinates'] = df_dobo_200['buffer_200'].apply(polygon_to_coordinates)
# 경도, 위도 생성
df_dobo_200['lon'] = df_dobo_200['geometry'].x
df_dobo_200['lat'] = df_dobo_200['geometry'].y
# 수요량(인구) 병합
df_dobo_200 = pd.merge(df_dobo_200, pop[['행정동코드명', 'a']], how= 'left', right_on = '행정동코드명', left_on = '읍면동명')
del df_dobo_200['행정동코드명'], df_dobo_200['노드 WKT']
# 노드 시각화용 데이터 생성
df_dobo_viz = df_dobo_200.iloc[:, 6:11]
df_dobo_viz = pd.DataFrame(df_dobo_viz, columns = df_dobo_viz.columns)
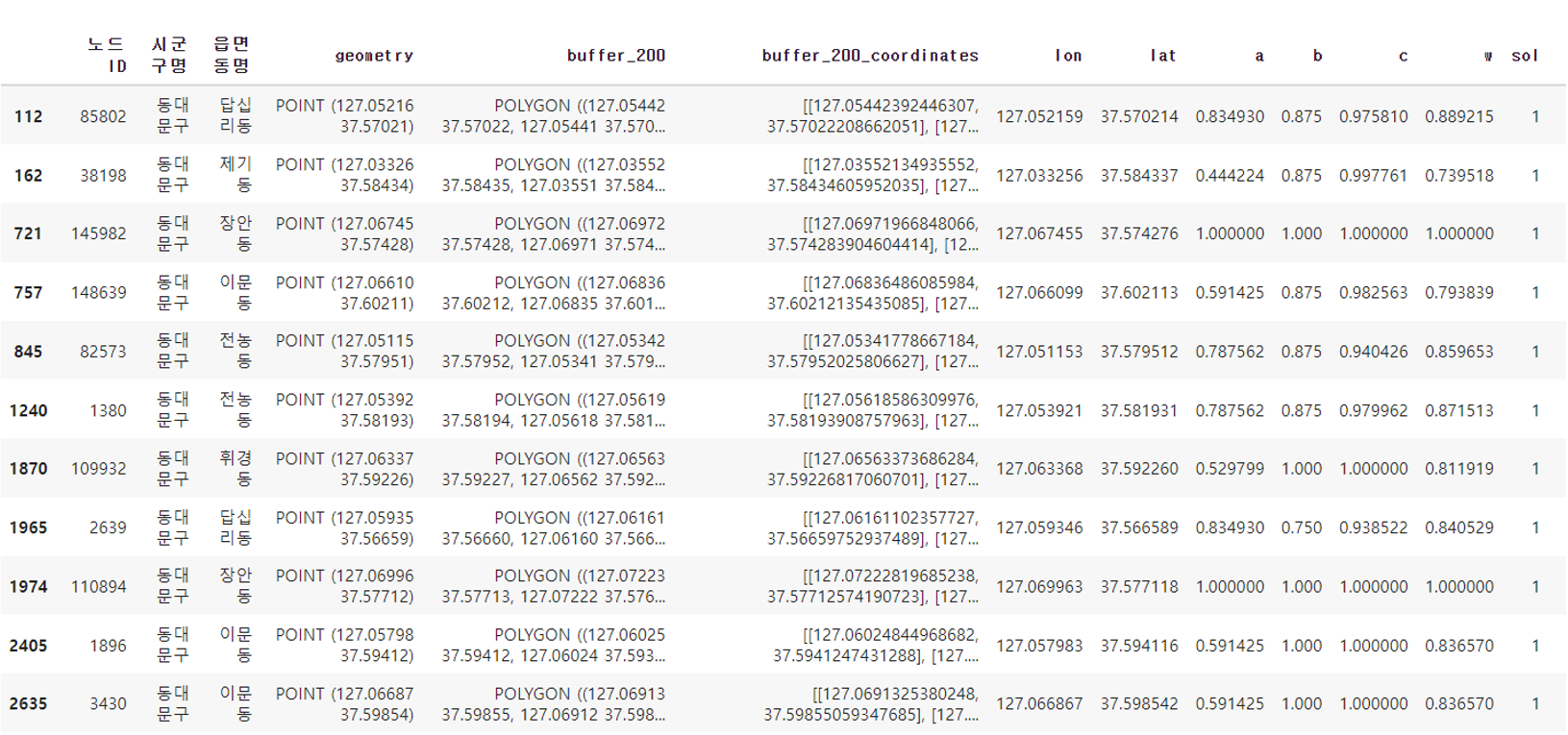
df_dobo_200.head(5)
노드 링크 데이터의 동대문구 모습을 시각화한 것은 다음과 같다.
중간의 데이터 수정 함수는 원천 데이터인 노드-링크 데이터의 오류로 규칙성이 있어 함수로 전처리 한 후 시각화를 하였다.
추후 교통량 시각화를 하고자 하는 사람들은 활용하길 바란다.
# 노드-링크 지도에 보여주기
df = pd.read_csv('./서울시 자치구별 도보 네트워크 공간정보.csv', encoding='cp949')
df = df[(df['노드링크 유형'] == 'LINK') &
(df['시군구명'] == '동대문구')]
# 용두동 + 신설동 = 용신동
df.loc[(df['읍면동명'] == "용두동") |
(df['읍면동명'] == "신설동"), "읍면동명"] = "용신동"
df.reset_index(drop=True, inplace=True)
# 데이터 오류 정정 후 geometry 형식 변환하는 함수
def wkt_to_geometry(string):
string = re.findall(r'\d+', string)
lst = []
lst.append([float(string[0] + '.' + string[1]), float(string[2] + '.' + string[3][:-3])])
for i in range(3, len(string), 3):
try:
lst.append([float(string[i][-3:] + '.' + string[i+1]), float(string[i+2] + "." + string[i+3][:-3])])
except:
continue
return lst
# 메모리 아웃 issue로 인한 데이터 컬럼 축소
df['geometry'] = df['링크 WKT'].apply(wkt_to_geometry)
df_link = df[['링크 ID','geometry']]
layer = pdk.Layer(
'PathLayer',
df_link,
get_path='geometry',
get_width=5,
get_color='[255, 255, 120]',
pickable=True,
auto_highlight=True
)
# 지도 시각화
layer2 = pdk.Layer(
'ScatterplotLayer',
df_dobo_viz,
get_position='[lon, lat]',
get_radius=7,
get_fill_color='[255, 0, 0]',
pickable=True,
auto_highlight=True)
center = [127.0400, 37.5744]
view_state = pdk.ViewState(
longitude=center[0],
latitude=center[1],
zoom=13)
r = pdk.Deck(layers=[layer, layer2], initial_view_state=view_state)
r.to_html('./wow.html')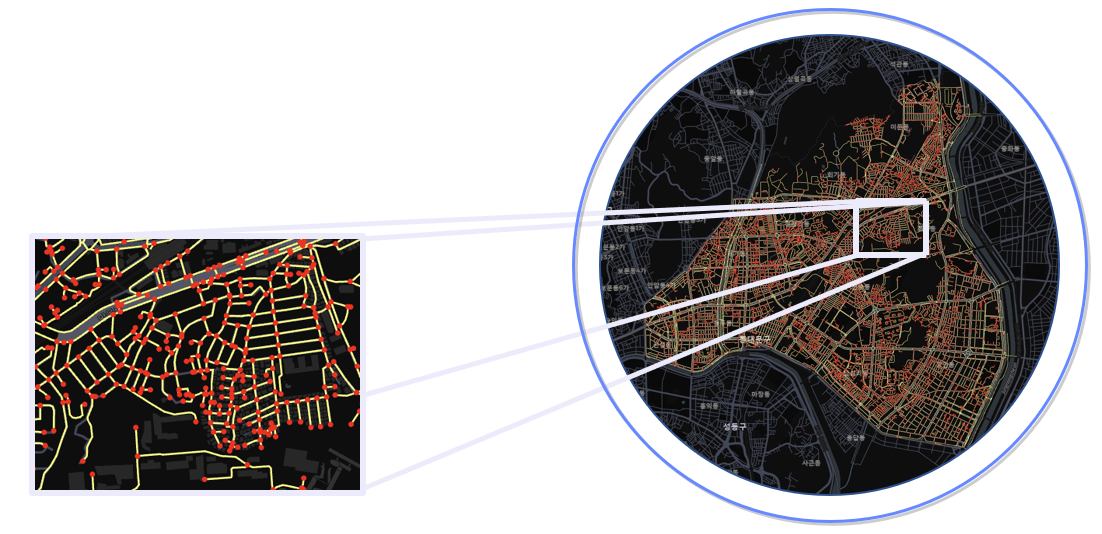
수요량 산출
MCLP 알고리즘은 각 수요지점들의 수요량들을 제한된 후보지점들의 커버리지를 기준으로 최대한 많이 커버하도록 후보지들을 선택하는 알고리즘이다.
여기서 수요지점과 후보지지점을 일치시켰으므로 수요지점인 도보 노드데이터들의 각 지점의 수요량을 잘 구해주면 된다.
수요량은 a, b, c의 weighted sum인 w로 사용하였다.
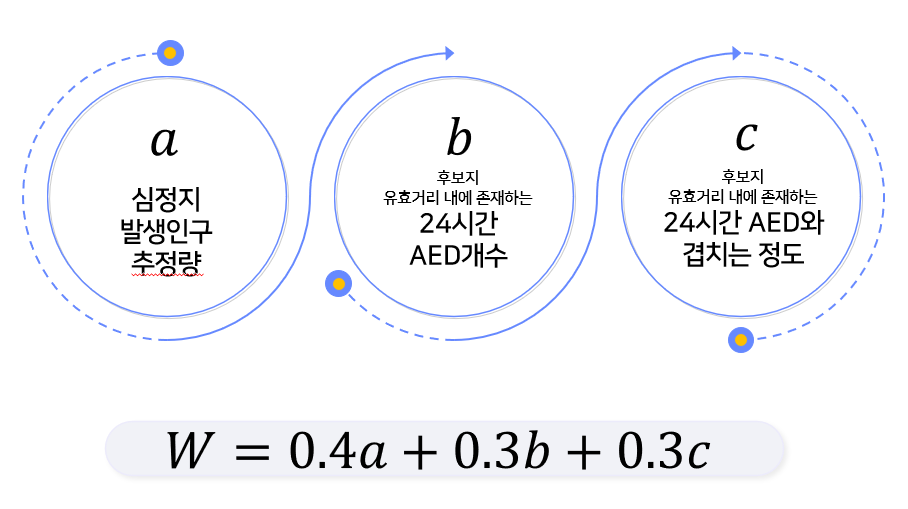
1. 심정지 발생인구 추정량(a)
- 성별, 연령대별 심정지 발생률이 다르므로 각 지역마다 다른 인구통계학적 정보를 0에서 1 사이의 상대적인 정보로 반영하였다.
pop = pd.read_csv('./동대문구_동별_연령대별_인구수.csv')
cols = pop.columns
pop['male'] = pop[cols[2]] * 0.01 + pop[cols[3]] * 0.026 + pop[cols[4]] * 0.039 + pop[cols[5]] * 0.075 + pop[cols[6]] * 0.139 + pop[cols[7]] * 0.7
pop['male'] = pop['male'] / pop['male'].max()
pop['female'] = pop[cols[8]] * 0.01 + pop[cols[9]] * 0.026 + pop[cols[10]] * 0.039 + pop[cols[11]] * 0.075 + pop[cols[12]] * 0.139 + pop[cols[13]] * 0.7
pop['female'] = pop['female'] / pop['female'].max()
pop['a'] = 0.64 * pop['male'] + 0.36 * pop['female']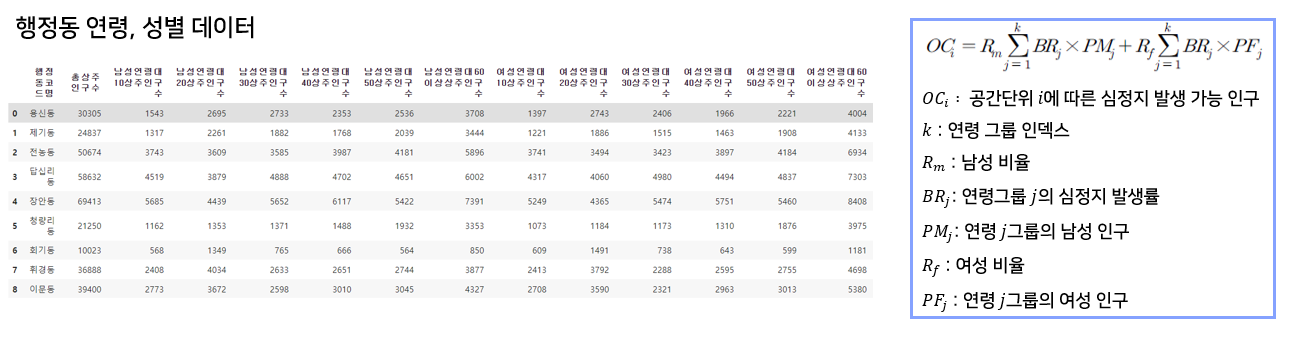
2. 유효거리 내 존재하는 24시간 AED 수(b)
- 기존 AED로 수요가 충족될수록 수요량이 작아지는 형태이다.
- 각 점에 100m 반경의 buffer를 생성하여 비교, 두 점의 원이 겹칠 경우 해당 후보지가 24시간 AED의 유효거리 내에 있음을 의미한다.
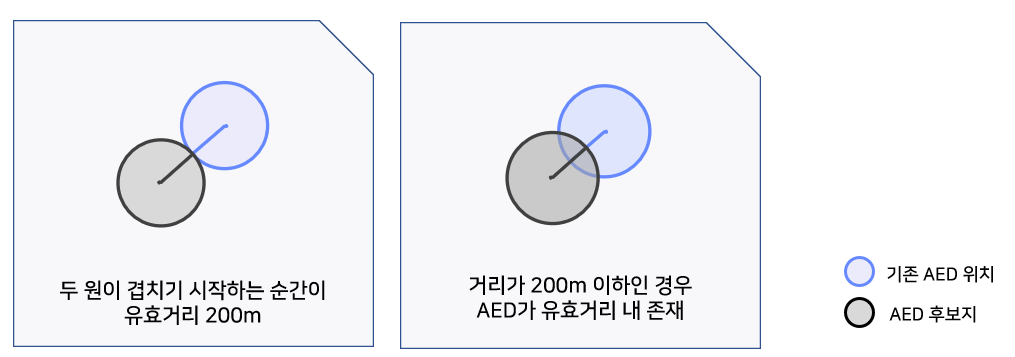
3. 유효거리 내 존재하는 24시간 AED와 겹치는 정도(c)
- 얼마나 기존 24시 AED와 겹치는지 정도를 의미한다.
- 겹치는 정도가 높을수록 수요가 더 충족되었음을 의미한다.
- 수요량 b가 잡아내지 못하는 정보를 반영 가능한다.

4. 최종 수요량 W
- w = 0.4a + 0.3b + 0.3c
- 수요량 b와 c는 서로 상호보완적인 관계이므로 같은 가중치를 주었다.
- 인구통계학적 특징인 a는 이 둘보단 더 많은 가중치를 주기 위하여 4:3:3 비율로 더해주었다.
total = pd.DataFrame()
for i in tqdm(df_dobo_100.index):
db = df_dobo_100.loc[i, 'buffer_100']
num = []
area = []
for j in aed_24_100.index:
aed = aed_24_100.loc[j, "buffer_100"]
num.append(db.intersects(aed))
if db.intersects(aed) == True:
area.append(db.intersection(aed).area)
info = {"intersects_num" : sum(num), "intersects_area" : sum(area)}
total = total.append(info, ignore_index=True)
# 정규화 및 최종 수요량 산출
total['intersects_num_scaled'] = (total['intersects_num'].max() - total['intersects_num']) / total['intersects_num'].max()
total['intersects_area_scaled'] = (total['intersects_area'].max() - total['intersects_area']) / total['intersects_area'].max()
df_dobo_200['b'] = total['intersects_num_scaled'].values
df_dobo_200['c'] = total['intersects_area_scaled'].values
df_dobo_200['w'] = 0.4 * df_dobo_200['a'] + 0.3 * df_dobo_200['b'] + 0.3 * df_dobo_200['c']
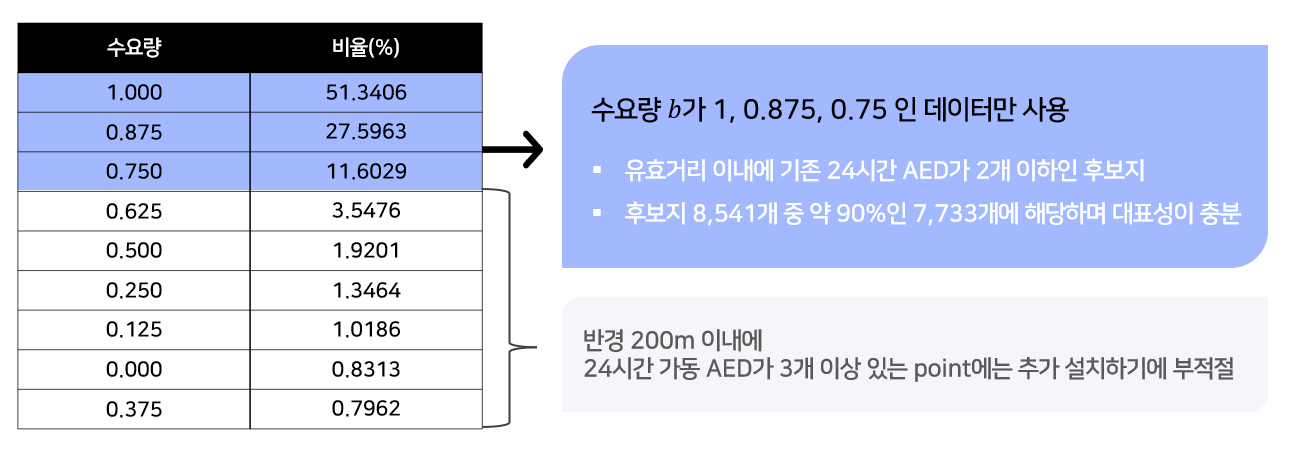
dobo_full = df_dobo_200.copy() # 설치 전 전체 커버리지 계산용, 밑에서 필터링 하기때문에 저장 필요 5. 수요량 b에 따른 최정 후보지 선정
- 유효거리 내에 기존 24시간 AED가 2개 이하로 존재하는 후보지만 사용한다.
- 이미 3개 이상의 AED로 커버되는 지점을 후보지로 사용하기엔 부적절하다. - 후보지 8,541개의 약 90%인 7,733개에 해당하여 대표성이 충분하다.
수요량 시각화
수요량을 기준으로 히트맵을 그려본 결과 AED 설치가 필요한 노란색 지점이 많은 것을 확인할 수 있었다.
heatmap_df = pd.DataFrame(dobo_full[['노드 ID', 'geometry', 'lon', 'lat', 'w']])
layer = pdk.Layer(
'ScatterplotLayer',
heatmap_df,
get_position='[lon, lat]',
get_radius=20,
get_fill_color='[255, 255 * w, 0]',
opacity = 0.5,
pickable=True,
auto_highlight=True)
# boundary layer
boundary_layer = pdk.Layer(
'PolygonLayer',
boundary,
get_polygon = 'coordinates',
get_fill_color = '[128, 128, 128]',
get_line_color = '[0,255,0]',
lineWidthScale = 20,
pickable = True,
auto_highlight = True,
opacity = 0.05
)
center = [127.0400, 37.5744]
view_state = pdk.ViewState(
longitude=center[0],
latitude=center[1],
zoom=13)
r = pdk.Deck(layers=[boundary_layer, layer], initial_view_state=view_state)
r.to_html('./wow.html')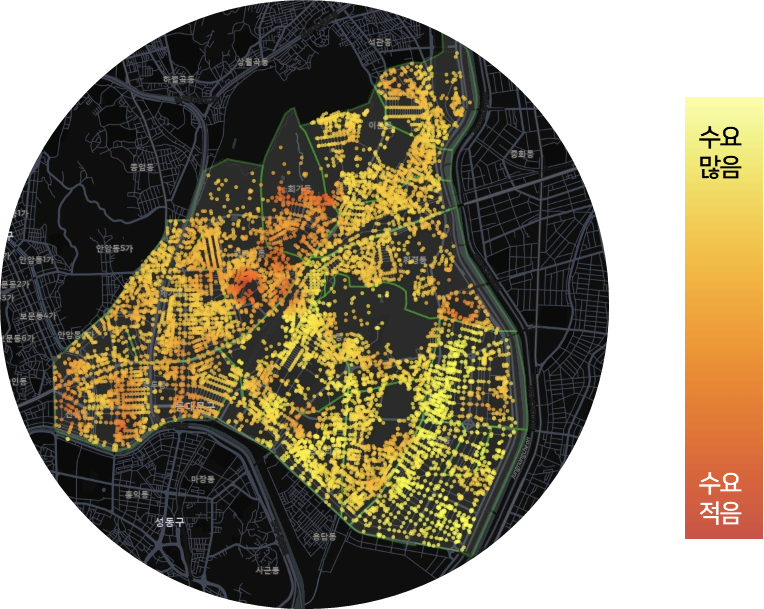
Modeling
MIP(Mixed Integer Programming)
- 파이썬 MIP라이브러리를 통해 혼합정수계획법의 최적화 문제로 정의하였다.
- 기존 존재하는 MCLP라이브러리도 존재하였으나 일반적인 상황(후보지 == 수요지)이 아니여서 직접 정의하는 방법을 선택하였다.
- 40개 추가 설치 기준으로 모델링엔 약 30분 정도 소요되었다.
# 수요지점으로부터 유효거리 내에 있는 후보지 집합 생성(제약조건 1)
cond_list = []
for i in tqdm(df_dobo_200.index):
buffer = df_dobo_200.loc[i, "buffer_200"]
lst = []
for j in df_dobo_200.index:
point = df_dobo_200.loc[j, "geometry"]
if point.within(buffer): # 200m 반경 기준으로 존재하는 주변 후보지 노드 ID 구하기
lst.append(df_dobo_200.loc[j, "노드 ID"])
cond_list.append(lst) # 해당 후보지를 커버할 수 있는 수요 point의 list, 집합 N
temp = df_dobo_200.copy()
temp['노드 ID'] = pd.to_numeric(temp['노드 ID'])
temp['w'].index = temp['노드 ID']
w = temp['w']
model = Model()
model.max_gap = 0.0
x = [model.add_var(name = "x%d" % i, var_type = BINARY) for i in temp['노드 ID']] # 제약 조건 3 : 포인트에 설치되는가
y = [model.add_var(name = "y%d" % i, var_type = BINARY) for i in temp['노드 ID']] # 제약 조건 4 : 포인트가 커버되는가
model.objective = maximize(xsum(w[i] * model.vars['y%d' %i] for i in temp['노드 ID'])) # 목적함수
model += xsum(model.vars['x%d' %j] for j in temp['노드 ID']) == 40 # 제약 조건 2 : 설치할 AED 개수
for num, idx in enumerate(temp['노드 ID']):
model += xsum(model.vars['x%d' %j] for j in cond_list[num]) >= model.vars['y%d' %idx] # 제약 조건 1 : cond_list(집합 N)에 속한 후보지 중 적어도 한 곳에 AED가 입지하면 i는 커버됨
start = time.time()
model.optimize()
solution = []
for j in temp['노드 ID']:
if model.vars['x%d' %j].x == 0:
solution.append(0)
else:
solution.append(1)
print(f"Time :{round(time.time() - start, 2)} s")
temp['sol'] = solution
sol = temp[temp['sol'] == 1]
sol['icon_data'] = None
for i in sol.index:
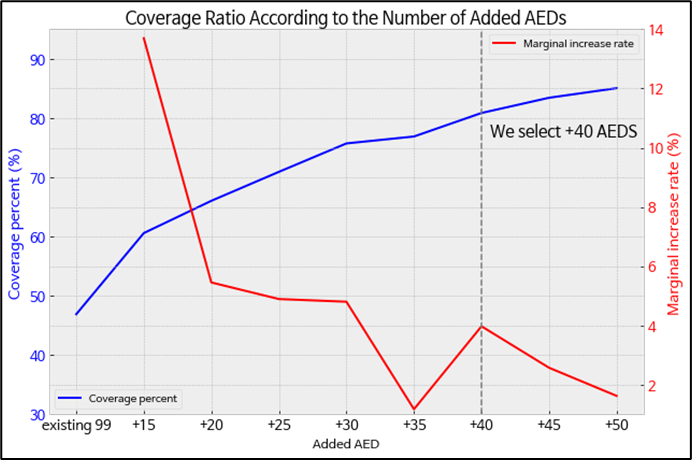
sol["icon_data"][i] = icon_dataAED 개수에 따른 커버리지 변화
- 실외 스마트 AED는 한 대당 300만 원이 소요되므로 경제적인 의사결정이 요구된다.
- 또한 추가 AED 개수가 증가함에 따라 커버리지의 한계 증가율은 체감되기 때문에 합리적인 개수 설정이 필요했다.
- 추가 AED 개수를 15개에서 50개까지 늘려본 결과 40개의 AED를 설치하는 것이 적절했다.
num = ['existing 99', '+15', '+20', '+25', '+30', '+35', '+40', '+45', '+50']
a = [46.89, 60.59, 66.04, 70.93, 75.73, 76.9, 80.87, 83.44, 85.06]
b = [None, 13.7, 19.15, 24.04, 28.84, 30.01, 33.98, 36.55, 38.17]
c = [None, 13.7, 5.45, 4.89, 4.8, 1.17, 3.97, 2.57, 1.62]
coverage = pd.DataFrame([num,a,b,c]).transpose()
coverage.columns = ['Added AED', 'Coverage percent', 'Coverage growth rate', 'Marginal increase rate']
plt.style.use('bmh')
fig, ax1 = plt.subplots(figsize=(9,6))
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
ax1.set_title('Coverage Ratio According to the Number of Added AEDs', fontsize=16)
ax1.set_xlabel('Added AED')
ax1.set_ylabel('Coverage percent (%)', fontsize=14, color='b')
ax1.plot(coverage['Added AED'], coverage['Coverage percent'], color='b', label='Coverage percent')
plt.ylim(30,95)
ax1.tick_params(axis='y', labelcolor='b')
plt.text(6.12,77,'We select +40 AEDS',size=15)
ax2 = ax1.twinx()
ax2.set_ylim(1,14)
ax2.set_ylabel('Marginal increase rate (%)', fontsize=14, color='r')
ax2.plot(coverage['Added AED'], coverage['Marginal increase rate'], color='r', label='Marginal increase rate')
ax2.tick_params(axis='y', labelcolor='r', labelsize=13)
plt.axvline(x='+40', color='gray', linestyle='--', linewidth=1.5)
ax1.legend(loc='lower left')
ax2.legend(loc='upper right')
fig.tight_layout()
Conclusion
최종 후보지 선정 결과
- 동대문구 내에 실외 AED 40개소 추가 설치한 결과 커버리지가 80.87%로 증가했다.
- 기존 99개로 46%를 커버하고 있던 것에 비교하면 합리적인 위치 선정이라고 볼 수 있다.
- 보라색은 기존 24시간 AED이고 노란색이 추가 설치된 AED 이다.
# 기존 24시간 AED
layer1 = pdk.Layer(
'PolygonLayer',
aed_24_200,
get_polygon='buffer_200_coordinates',
get_fill_color= '[216, 157, 227, 89]',
get_fill_line=[255, 255, 255, 100],
pickable=True,
auto_highlight=True)
layer2 = pdk.Layer(
"IconLayer",
aed_24_200,
get_icon="icon_data",
get_size=8,
size_scale=3,
get_position='[lon, lat]',
pickable=True,
auto_highlight=True
)
# 새롭게 추가된 AED
layer3 = pdk.Layer(
'PolygonLayer',
sol,
get_polygon='buffer_200_coordinates',
get_fill_color = '[225, 225, 0, 130]',
get_fill_line = [255, 255, 255, 100],
pickable=True,
auto_highlight=True)
layer4 = pdk.Layer(
'IconLayer',
sol,
get_icon="icon_data",
get_size=8,
size_scale=3,
get_position='[lon, lat]',
pickable=True,
auto_highlight=True
)
center = [127.0400, 37.5744]
view_state = pdk.ViewState(
longitude=center[0],
latitude=center[1],
zoom=13)
r = pdk.Deck(layers=[layer1, layer2, layer3, layer4], initial_view_state=view_state)
r.to_html('./wow.html')
시사점 및 한계점
시사점
- 동대문구의 기존 24시간 가동 AED가 커버하지 못한 지역을 각 후보point의 수요에 기반하여 최적의 위치에 설치하였다.
- 도보 노드 point를 활용하여 기존 실내에 치우쳐져 있던 AED에 대한 24시 접근성을 향상시켰다.
- 행정동마다 다른 성별, 연령대별 심정지 위험 정도를 고려하여 수요를 반영하였다.
- 수요량 예측 시 기존 AED 개수 뿐만 아니라 면적까지 고려해 24시 AED 사각지대를 최소화하였다.
한계점
- 동대문구 내의 8,000개가 넘는 도보 노드 point에 하나하나 매핑시킬 방법을 찾지 못했다. 따라서 심정지 발생가능 인구를 추정하고 후보지 수요에 반영하는 정도가 행정동 단위로 한정되었다.
- 실제 보행자가 많이 다니는 지역임에도 도보 노드 point가 부족한 경우 정확한 수요량 예측 불가하였다.
(ex) 서울시립대학교 캠퍼스는 6시 이후에도 사람이 많지만 수요지점이 존재하지 않아 커버되지 못하였다.)
마무리
- 수업 듣는 도중 교수님의 홍보로 참가하게 된 대회인데 처음 1등을 해봐서 얼떨떨하다...
- 한달 동안 꽤 많은 시간을 투자하면서 다듬고 다듬은 결과인 것 같다.
- 언제나 그랬듯 전처리 과정에서 많은 시행착오가 있었는데 이전 서울시 핫플레이스 시각화 때 다뤘던 pydeck이 많은 도움이 되었다.
- 하지만 좌표계 변경 후 거리계산이나 최적화 프로그래밍같은 생소한 부분에서 많은 시간을 할애해야 했다.
- 앞으로 지도 데이터는 좀 더 자신있게 다룰 수 있게 되었다.
대회 준비과정에서 얻은 가장 큰 교훈은 '문제를 정확하게 정의하는 것'이 얼마나 중요한지 깨달은 것이다. 많은 시행착오 중에서도 길을 잃지 않았던 것은 처음부터 하고자 하는 바가 확실했고, 데이터와 근거가 확실했으며, 전체적인 흐름이 간단명료했기 때문이였다.
- 꽤 큰 상금보다 앞으로의 프로젝트에서 항상 기억하고 갖춰야할 덕목을 얻은 것에 더 만족한 의미있는 대회였다.
활용 데이터 목록 및 참고문헌
활용 데이터 목록

참고문헌
- 현성열, 장재호, 김진주, 양혁준 and 김우진. (2012). 병원 전 심정지 환자를 대상으로 한 제세동 횟수와 생존율 및 신경학적 예후와의 연관성. Acute and Critical Care, 27(4), 263-268.
- 김감영. (2021). 공간 최적화 모형을 이용한 자동심장충격기(AED)의 커버리지 평가: 강남구를 사례로. 한국지리학회지, 10(1), 153-166.
- 백승렬 and 김준현. (2020). 대구시 자동심장충격기 공간분포 특성에 따른 공공 거점후보지 선정 연구. 한국측량학회지, 38(6), 599-610.
- Kwon, Pil, Lee, Young Min, Yu, Ki Yun, & Lee, Won Hee. (2016). A Study of Optimal Location and Allocation to Improve Accessibility of Automated External Defibrillator. Journal of the Korean Society of Surveying, Geodesy, Photogrammetry and Cartography, 34(3), 263–271.
- 광주소방 안전본부 겨울철 심정지 환자 발생 분석 결과보고
- 2006~2019 급성심장정지조사 통계. 보건복지부「 자동심장충격기의 배신…꼭 필요한 새벽에 못 쓴다, https://shindonga.donga.com/3/all/13/2106307/1
- Lucm의 smart aed ( http://lucm.co.kr/smart-aed/ )
- AED icon made by kanyanee-watanajitkasem, https://www.flaticon.com/kr/authors/kanyanee-watanajitkasem