1 문제

열심히 도전하다가 결국 못 풀고 풀이를 봤다... 이걸 보고 어떻게 곱셈을 떠올리는지...
2 문제 해결 알고리즘
- 독해: 문제를 읽고 이해한다.
- 재정의+추상화: 문제를 익숙한 용어로 재정의한다.
- 설계: 어떻게 해결할지 계획을 세운다.
- 검증: 계획을 검증한다.
- 구현: 프로그램을 구현한다.
- 회고: 어떻게 풀었는지 돌아보고, 개선할 방법이 있는지 찾아본다.
2-1 독해
결국 멤버와 팬의 성별이 모두 M인 경우의 여집합의 개수를 세야한다.
2-2 재정의+추상화
멤버와 팬 배열이 서로 교차하며 지나갈 때... 멤버와 팬의 성별 중 적어도 하나가 둘다 M이 아닌 경우의 수를 세면 된다. 멤버가 팬 위에서 오른쪽으로 지나간다고 생각하면 편한 것 같다.
2-3 설계
2-3-a 직관
우선 수식으로 접근하여... sz(fans) - sz(members) + 1 - "순회 중 적어도 한 쌍이 MM일 경우"를 구하면 된다.
2-3-b 체계적인 접근
2-3-b-1 비슷한 문제?
푼 적이 없다.
2-3-b-2 단순한 방법에서?
요런 식으로 풀면 된다.
for (int i = 0; i < n - m; ++i) {
for (int j = 0; j < m; ++j) {
if (member[i + j] == `M` && fans[j] == `M`) ret++;
}
}허나 이렇게 풀면 시간 복잡도는 O(NM-M^2)... 20만인 인풋을 고려해 보았을 때 풀기 어려워보인다.
2-3-b-3 결국... 책의 풀이를 보고 마는데
아하! 곱셈을 활용하여 문제를 해결할 수 있다. 왜 그런가?
M를 1로 놓고 F를 0으로 놓자. 왜냐하면 우리는 둘 다 M인 경우를 제하고 나머지 경우를 세야 하므로 곱연산을 한 결과에서 0의 개수를 세면 된다. (둘 다 M인 경우는 곱 연산을 하면 1x1=1이 나오므로...)
설명은 여기를 참고한다.
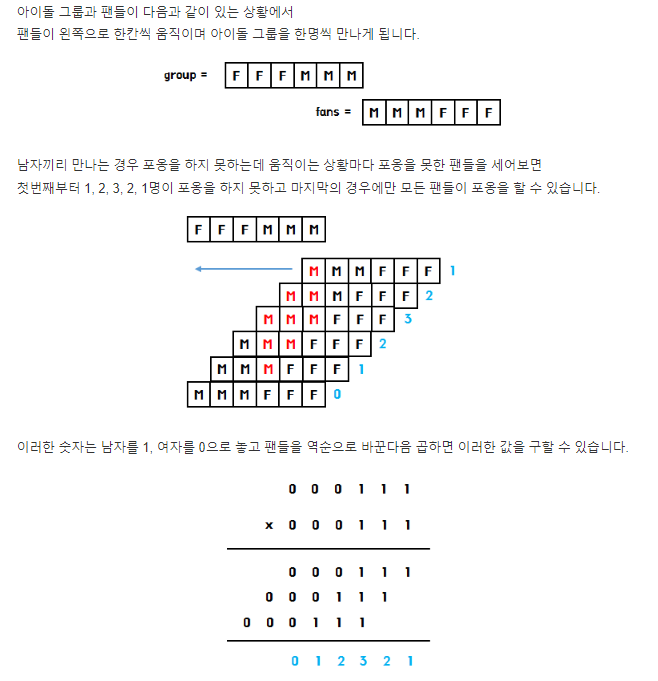
따라서 곱연산을 하여 각 자리수의 결과를 저장한 다음, 자리수가 0인 경우만 체크하면 허그를 하는 개수를 셀 수 있다!
2-4 검증
2-4-b-1 곱셈을 통해 직접 세는 알고리즘
이때 곱 연산을 하는 알고리즘을 초등학생 때 곱셈하듯이 하면 O(NM-M^2)이 뜬다... N과 M은 각각 20만에 달하는 수이므로 4백억, 1억의 법칙에 의거하여 4백초가 걸린다. 따라서 시간 내에 해결할 수 없다.
2-4-b-2 카라츠바 곱셈 알고리즘
카라츠바 알고리즘은 O(n^lg3)의 시간 복잡도로 문제를 해결할 수 있다. 따라서 시간 안에 문제를 해결할 수 있다.
2-5 구현
카라츠바 곱셈 알고리즘을 이용하여 구현했다.
#include <bits/stdc++.h>
#define endl "\n"
#define all(x) (x).begin(), (x).end()
#define sz(x) (uint)(x).size()
using namespace std;
using lld = long long;
using pii = pair<int, int>;
using pll = pair<lld, lld>;
void printVector(vector<int> v) {
for (int i = 0; i < sz(v); ++i) {
cout << v[i] << " ";
}
cout << endl;
}
void cTimes(vector<int> &a, vector<int> &b, int c) {
int an = sz(a), bn = sz(b);
if (bn == 0 || c == 0) return;
for (int i = 0; i < sz(a); ++i) {
a[i] += c * b[i];
}
}
vector<int> multiply(vector<int> &a, vector<int> &b) {
int an = sz(a), bn = sz(b);
vector<int> c(an + bn, 0);
for (int i = 0; i < an; ++i) {
for (int j = 0; j < bn; ++j) {
c[i + j] += a[i] * b[j];
}
}
return c;
}
void addTo(vector<int> &a, vector<int> &b, int k) {
int an = sz(a), bn = sz(b);
if (bn == 0) return;
if (an < bn + k) a.resize(bn + k, 0);
for (int i = k; i < bn + k; ++i) a[i] += b[i - k];
}
void subFrom(vector<int> &a, vector<int> &b) {
int an = sz(a), bn = sz(b);
if (bn == 0) return;
for (int i = 0; i < bn; ++i) a[i] -= b[i];
}
vector<int> karatsuba(vector<int> &a, vector<int> &b) {
// cout << "{" << endl;
int an = sz(a), bn = sz(b);
// cout << "an " << an << " " << "bn " << bn << endl;
if (an < bn) return karatsuba(b, a);
if (an == 0 || bn == 0) return vector<int>();
else if (an == 1) { vector<int> ret(bn, 0); cTimes(ret, b, a[0]); return ret; }
else if (bn == 1) { vector<int> ret(an, 0); cTimes(ret, a, b[0]); return ret; }
else if (an <= 50) return multiply(a, b);
int midIdx = an / 2;
vector<int> a0(a.begin(), a.begin() + midIdx);
vector<int> a1(a.begin() + midIdx, a.end());
vector<int> b0(b.begin(), b.begin() + min<int>(sz(b), midIdx));
vector<int> b1(b.begin() + min<int>(sz(b), midIdx), b.end());
vector<int> z2 = karatsuba(a1, b1);
vector<int> z0 = karatsuba(a0, b0);
addTo(a0, a1, 0);
addTo(b0, b1, 0);
vector<int> z1 = karatsuba(a0, b0);
subFrom(z1, z0);
subFrom(z1, z2);
vector<int> ret;
addTo(ret, z0, 0);
addTo(ret, z1, midIdx);
addTo(ret, z2, 2 * midIdx);
// printVector(ret);
// cout << '}' << endl;
return ret;
}
int hugCnt (string members, string fans) {
int mn = sz(members), fn = sz(fans);
vector<int> membersVector(mn), fansVector(fn);
for (int i = 0; i < mn; ++i) {
if (members[i] == 'M') membersVector[mn - 1 - i] = 1;
else membersVector[mn - 1 - i] = 0;
}
for (int i = 0; i < fn; ++i) {
if (fans[i] == 'M') fansVector[i] = 1;
else fansVector[i] = 0;
}
// printVector(membersVector);
// printVector(fansVector);
vector<int> karatsubaMembersAndFans = karatsuba(membersVector, fansVector);
// printVector(karatsubaMembersAndFans);
int ret = 0;
for (int i = mn - 1; i < fn; ++i) {
if (karatsubaMembersAndFans[i] == 0) ret++;
}
return ret;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int c;
cin >> c;
while (c--) {
string members, fans;
cin >> members >> fans;
cout << hugCnt(members, fans) << endl;
}
return 0;
}카라츠바 알고리즘의 구현은 여기를 참고했다.
결과는?

성공!~ (사실 언제 초등학교 식 곱셈을 정할지에 대해서 분분했지만... 50 정도로 설정하니 문제를 잘 해결할 수 있었다.)
2-6 회고
2-6-1 두 개의 배열을 비교하며 And 연산을 할 경우
곱셈을 떠올릴 수 있어야 한다. 정확히는, 곱셈 결과에서 0을 세는 경우도 고려할 수 있어야 한다. 이 작은 아이디어가 해당 문제를 푸는 핵심이었다.
두 개의 배열을 비교하며 각 원소에 대해 And 연산을 할 경우, 곱셈을 떠올릴 수 있어야 한다! 곱셈 결과에서
0을 세는 방법을 해당 문제를 푸는데 사용할 수 있다.
2-6-2 벡터를 또 다른 벡터로부터 정의하는 방법
벡터는 다른 벡터의 값을 복사하며 정의할 수도 있다. 반복자를 이용하여 정의한다.
벡터는 다른 벡터의 값을 복사하며 정의할 수도 있다. 반복자를 이용하여 정의한다. 문법은 다음과 같다.
vector<int> vect1{ 10, 20, 30 }; vector<int> vect2(vect1.begin(), vect1.end());
3 구종만's Sol
3-1 카라츠바 알고리즘을 이용한 구현
위에 내가 작성한 코드와 거의 동일하다. 그럼 다른 점은? hugs() 함수가 아주 약간 다르다.
int hugs(const string& members, const string& fans)
{
int N = members.size(), M = fans.size();
vector<int> A(N), B(M);
for (int i = 0; i < N; i++) {
A[i] = (members[i] == 'M');
}
for (int i = 0; i < M; i++) {
B[M - i - 1] = (fans[i] == 'M');
}
int ret = 0;
vector<int> res = karatsuba(B, A);
for (int i = 0; i < res.size(); i++) {
cout << res[i] << ' ';
}
for (int i = N - 1; i < M; i++) {
if (res[i] == 0) ret++;
}
cout << endl;
return ret;
}중간에 입력을 받는 부분을 보면 A[i] = (members[i] == 'M');로 깔끔하게 처리한 것을 볼 수 있다.
3-2 구종만's Sol을 읽고 또 회고
3-2-1 bool로 bool을 정의하지 말자.
대표적인 코드의 가독성을 망가뜨리는 주범이다. 만약 조건문으로 if문을 처리하고, if문 내부가 해당 조건문에 따라 0 또는 1을 대입한다면 또는 직접적으로 해당 조건문을 활용한다면, 또한 그 코드 내부가 비교적 단순하다면, 해당 조건문을 그대로 쓰는 방법을 고려하자.
만약 조건문으로 if문을 처리하고, if문 내부가 해당 조건문에 따라 0 또는 1을 대입한다면 또는 직접적으로 해당 조건문을 활용한다면, 또한 그 코드 내부가 비교적 단순하다면, 해당 조건문을 그대로 쓰는 방법을 고려하자.
이전for (int i = 0; i < mn; ++i) { if (members[i] == 'M') membersVector[mn - 1 - i] = 1; else membersVector[mn - 1 - i] = 0; } for (int i = 0; i < fn; ++i) { if (fans[i] == 'M') fansVector[i] = 1; else fansVector[i] = 0; }이후
for (int i = 0; i < N; i++) { A[i] = (members[i] == 'M'); } for (int i = 0; i < M; i++) { B[M - i - 1] = (fans[i] == 'M'); }
4 끝
답안을 보고 풀어서 그런지 배운게 많이 없는 것 같다... 복습해야지
