[알고리즘 문제 해결 전략] 07.2 문제: 쿼드 트리 뒤집기 (문제 ID: QUADTREE)

Daniel Oh·2023년 12월 31일

algorithm algospot ps

알고리즘 문제 해결 전략

목록 보기

6/7

1 문제

1트 만에 성공했다. 물론 테스트 케이스를 모두 통과하는 함수를 구현하는데 좀 걸리긴 했지만...

2 문제 해결 알고리즘

독해: 문제를 읽고 이해한다.

재정의+추상화: 문제를 익숙한 용어로 재정의한다.

설계: 어떻게 해결할지 계획을 세운다.

검증: 계획을 검증한다.

구현: 프로그램을 구현한다.

회고: 어떻게 풀었는지 돌아보고, 개선할 방법이 있는지 찾아본다.

2-1 독해

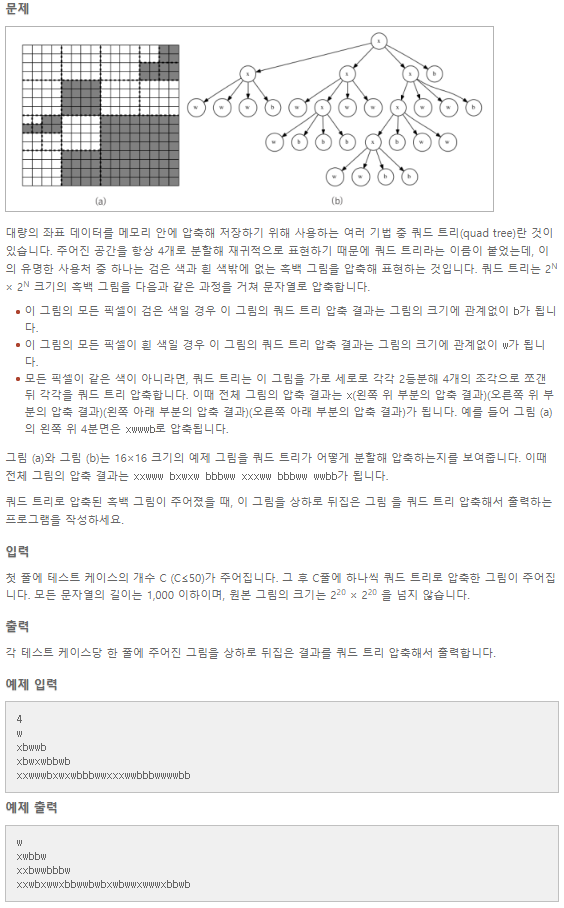
쿼드 트리 라는 그림 압축 기법이 있는데, 이는 이미지를 문자열로 압축하는 기법이다. 만약 주어진 그림이 흑색 또는 백색으로 단일할 경우 각각 b와 w로, 단일하지 않다면 4분면으로 나누고 1사분면 2사분면 3사분면 4사분면을 x 뒤에 붙인다.

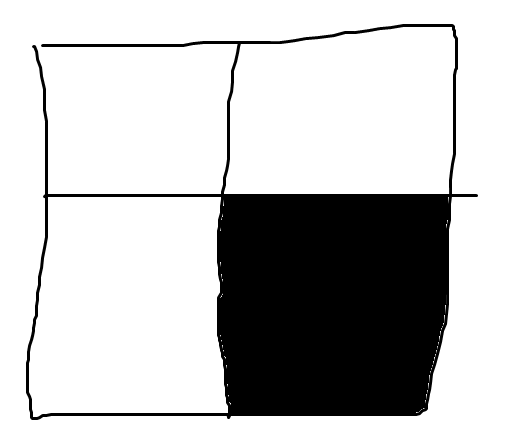
위와 같은 그림은 xwwwb 와 같이 압축될 것이다.

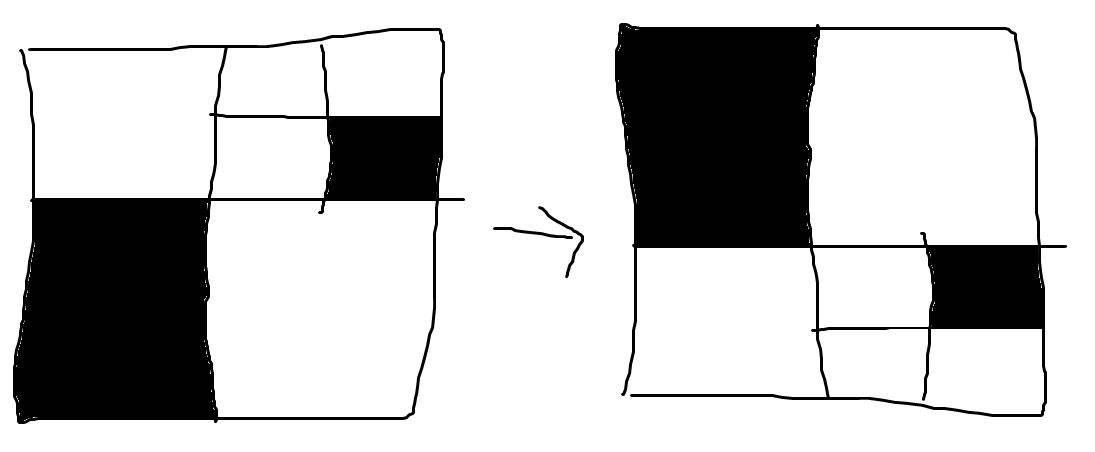
쿼드 트리 압축 문자열이 주어질 때, 해당 그림을 위아래로 뒤집은 (flip) 그림의 쿼드 트리 압축 문자열을 출력하라는 문제이다.

예를 들어, xwxwwwbbw가 주어지면, xbwwxwbww를 출력해야 한다. (이해를 돕기 위해 괄호를 추가하면 xw(xwwwb)bw -> xbww(xwbww)이다.)

만약 주어진 그림이 단일할 경우 b와 w로, 단일하지 않다면 ...를 x 뒤에 붙인다.: 만약 주어진 문자열의 길이가 1이면 뒤집기 위해서 그대로를 반환하면 되고, 주어진 문자열의 길이가 1 이상이면 무조건 x로 시작함을 시사한다. 즉 어떤 쿼드 트리 문자열도 wb 이런 건 될 수 없다.

해당 그림을 위아래로 뒤집기 (flip): 단순히 쿼드 트리 문자열의 관점에서 생각해본다면, 1사분면 2사분면에 있던 내용과 3사분면 4사분면에 있던 내용과 교체하면 된다. 따라서 길이가 1 이상인 (x로 시작하는) 쿼드 트리 문자열이 주어질 때 1사분면에 있는 내용, 2사분면에 있는 내용, 3사분면에 있는 내용, 4사분면에 있는 내용을 각각 추출하여 구분해야 함을 알 수 있다.

2-2 재정의+추상화

문자열이 주어졌을 때, 문자열을 위아래로 뒤집는 함수는: 결국 안에 있는 모든 x 이하의 쿼드 트리에 대하여 1,2 사분면과 3,4 사분면을 교체하면 된다.

xwxwwwbbw가 주어지면, xbwwxwbww를 출력
1. x(w)(xwwwb)(b)(w) -> x(b)(w)(w)(xwwwb)
2. x(b)(w)(w)(xwwwb) -> x(b)(w)(w)(xwbww)

~~먼가 분할 정복의 냄새가 난다... 만약 x를 발견하면 그 아래에 대하여 또 재귀를 호출하되, 문자열의 나머지 부분을 인자로 넘겨주어야 할 것 같다.~~ <- 설계 부분에서 자세히 설명해보겠다.

2-3 설계

2-3-a 직관

분할 정복의 냄새가 난다... 문자열이 주어졌을 때, 뒤집힌 문자열을 뱉는 함수는 다음과 같다.

만약 주어진 문자열의 길이가 1이라면 단일하다는 뜻이므로 문자열 그대로를 뱉는다.
1이 아니라면 무조건 x로 시작한다. x 다음 부분을 4분면으로 각각 추출해야 한다.
1. 만약 x가 아니면 (w나 b이면) 그대로 4분면 벡터에 추가한다.
2. 만약 x라면 해당 영역의 뒤집힌 문자열을 4분면 벡터에 추가한다.
1,2사분면과 3,4사분면을 교체한다.
x + 사분면 벡터 문자열 을 반환한다.

재귀와 분할 정복의 차이점은 무엇일까?: 결국 분할 정복은 재귀에서 파생된 것이다. 대신 재귀 함수는 자기자신을 호출하며 처리된 결과를 어딘가에 기록하고 이 기록지를 토대로 다음 호출 결과가 바뀌는 반면, 분할 정복은 탐색하고자 하는 범위가 호출하는 시점에서 정해진다는 디테일한 차이가 있는 것 같다. 따라서 재귀 함수는 많은 경우에 선형적으로 문제를 해결하는 반면, 분할 정복은 로그 스케일과 같이 더 빠르게 문제를 해결할 수 있다. (물론 반례도 많이 존재하나, 이해를 위해...)

2-3-b 체계적인 접근을 위한 질문들

2-3-b-1 비슷한 문제?

없다... 굳이 따지자면 fastSum() 함수 구현? 근데 이것도 문자열을 다루진 않기 때문에 비슷하다고 보기엔 무리가 있을 것 같다. fastSum() 함수 구현에 대한 내용은 다음과 같다.

2-3-b-2 단순한 방법에서?

진짜 단순한 방법은... 주어진 문자열로 그림을 그리고, 위아래로 뒤집고, 다시 쿼드 트리 문자열로 압축하면 된다.

이를 위해서는

그릴 정사각형 2차원 배열을 2^x의 개수 사이즈으로 만들고, (물론, 이것은 최악의 경우를 상정한 것이나 최적화된 해를 찾기란 어려워보이니 그냥 가자.)
x가 나올 때마다 1사분면 2사분면 3사분면 4사분면을 칠하면 된다. 칠하는 함수는 x좌표, y좌표, 길이를 인자로 받아야 할 것이다.
다 그려지면 해당 그림을 위아래로 뒤집는다. 새로운 2차원 배열을 만들어서 역순으로 행을 담거나, 아니면 tempRow 변수를 만들어 row[i] 저장하고 row[i] = row[n-1-i]하고 row[n-1-i] = tempRow 하면 될 것이다.
뒤집어진 그림을 다시 쿼드 트리 문자열로 압축한다. 이는 단일한지 검사하고, 단일하지 않으면 x 뒤에 1사분면, 2사분면, 3사분면, 4사분면 내용을 붙이면 된다. 이는 재귀함수로 돌리면 될 것이다.

하지만 이렇게 풀면... 재귀 함수 문제 같아 보인다. 하지만 머, 이렇게도 풀리긴 할 것 같다. (허나 검증 단계에서 이런 풀이는 허용되지 않음을 보일 수 있을 것 같다.)

2-4 검증

2-3-a 직관

이때의 시간복잡도는 최악의 경우 w와 b가 번갈아가며 나오는, 마치 바둑판과 같은 모습일 것이다. 많이 쪼개져 있어야 뒤집는 문자열을 반환하는 함수 호출을 많이 할 것이므로...

원본 그림의 최대 크기는 2^20 x 2^20, 따라서 해당 크기의 그림에서w와 b가 번갈아가며 나오면... 뒤집는 문자열을 반환하는 함수는 x가 나올 때마다 호출된다.

만약 한 크기가 2^0이면 0, 2^1이면 1, 2^2이면 (1+2^2), 2^3이면 (1+2^2+2^4)이므로...
한 크기가 2^20이면 (2^0 + 2^2 + ... + 2^38) 번 호출될 것이다. 이는 등비수열 합 공식에 의하여 1*(4^20 - 1)/(4-1), 상수 배를 제외하면 4^20 = 2^40 = 2^13 * 2^27이 남는다. 2^27이 약 1억이고 1억번 연산하는데 1초 걸림을 고려할 때, 이 프로그램은 최악의 경우 2^13초 걸린다.

허허허 이러면 절.대.로. 주어진 시간 (10초) 안에 풀 수가 없다.

모든 문자열은 길이가 1000 이하임을 이용하면 어떨까? 최악의 경우는 길이가 1000인 문자열이 x(x....)(x....)(x....)(x....)임을 알 수 있다. 길이는 이때 쪼개진 횟수를 n이라고 하면 a0=1, a1=1+4, a2=1+4*(1+4), ...로, an=1+4*an-1이다. 계산의 편의를 위해 an=4^n로 놓겠다. an < 1000을 만족시키는 최대의 n을 찾아보면 4^5=1024이므로 4^4이 최대일 것이다!, 따라서 n=4이고, x의 개수 bn=an-1이므로 x 최대의 개수는 4^3일 것이다. 이는 2^6 =64개로, 함수는 64번 호출된다. 따라서 문제를 해결할 수 있다!

2-4-b-2 단순한 방법에서?

그릴 정사각형 2차원 배열을 2^x의 개수 사이즈으로 만들고, (물론, 이것은 최악의 경우를 상정한 것이나 최적화된 해를 찾기란 어려워보이니 그냥 가자.)

x가 나올 때마다 1사분면 2사분면 3사분면 4사분면을 칠하면 된다. 칠하는 함수는 x좌표, y좌표, 길이를 인자로 받아야 할 것이다.

다 그려지면 해당 그림을 위아래로 뒤집는다. 새로운 2차원 배열을 만들어서 역순으로 행을 담거나, 아니면 tempRow 변수를 만들어 row[i] 저장하고 row[i] = row[n-1-i]하고 row[n-1-i] = tempRow 하면 될 것이다.

뒤집어진 그림을 다시 쿼드 트리 문자열로 압축한다. 이는 단일한지 검사하고, 단일하지 않으면 x 뒤에 1사분면, 2사분면, 3사분면, 4사분면 내용을 붙이면 된다. 이는 재귀함수로 돌리면 될 것이다.

2차원 배열의 최대 크기는 2^20 x 2^20이다. 따라서 2^40*2의 메모리 크기가 필요하다. 허나 주어진 메모리 크기는 64MB로 2^6*2^20*2^3=2^29이다. 따라서 메모리 초과가 뜰 것이다. ㅋㅋ ㅠ

2-5 구현

2-3-a 직관에서 기술했던 설계를 구현해보자!

string flipUpDown(string line) {
    
    if(sz(line) == 1) return line;

    vector<string> quad;
    string quadItem = "";
    int i = 1;
    while (i < sz(line)) {
      if(sz(quad) == 4) break;
      if (line[i] != 'x') {
        quadItem = line[i];
        i += 1;
      } else {
        quadItem = flipUpDown(line.substr(i));
        i += sz(quadItem);
      }
      quad.push_back(quadItem);
    }

    string fst = quad[0];
    string scd = quad[1];
    quad[0] = quad[2];
    quad[1] = quad[3];
    quad[2] = fst;
    quad[3] = scd;
    
    return 'x' + vectorStringToString(quad);
}

만약 주어진 문자열의 길이가 1이면 그대로 반환한다. (뒤집을 것이 없으므로...)
만약 1에서 반환되지 않았다면 4분면으로 쪼개진다는 뜻이므로 4분면을 저장할 벡터 quad를 정의한다.
문자열을 순회하며 각 분면을 quad에 push한다.
1. 만약 사분면이 다 채워졌으면 멈춘다.
2. 만약 x로 시작하지 않으면 해당 문자를 quad에 넣는다.
3. 만약 x로 시작하면 나머지 문자열을 뒤집은 결과를 quad에 넣는다.
사분면이 다 채워지면 1,2사분면과 3,4사분면을 교체한다.
x에 quad벡터를 모두 이은 단일 문자열을 붙여 반환한다.

작성한 총 코드는 다음과 같다.

#include <bits/stdc++.h>
#define endl "\n"
#define all(x) (x).begin(), (x).end()
#define sz(x) (uint)(x).size()
using namespace std;
using lld = long long;
using pii = pair<int, int>;
using pll = pair<lld, lld>;

string vectorStringToString(vector<string> v) {
    string result = "";
    for (string s : v) {
        result += s;
    }
    return result;
}

string flipUpDown(string line) {
    
    if(sz(line) == 1) return line;

    vector<string> quad;
    string quadItem = "";
    int i = 1;
    while (i < sz(line)) {
      if(sz(quad) == 4) break;
      if (line[i] != 'x') {
        quadItem = line[i];
        i += 1;
      } else {
        quadItem = flipUpDown(line.substr(i));
        i += sz(quadItem);
      }
      quad.push_back(quadItem);
    }

    string fst = quad[0];
    string scd = quad[1];
    quad[0] = quad[2];
    quad[1] = quad[3];
    quad[2] = fst;
    quad[3] = scd;
    
    return 'x' + vectorStringToString(quad);
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int n;
    cin >> n;

    while(n--) {
        string l;
        cin >> l;
        cout << flipUpDown(l) << endl;;
    }

    return 0;
}

결과는?

성공~

좋은 코드를 작성하기 위한 원칙 적용

적극적으로 코드 재사용: 문자열 벡터를 받았을 때 문자열을 모두 이은 단일 문자열을 반환하는 함수 vectorStringToString()을 정의하였다.
표준 라이브러리 공부: vector<string>을 적극적으로 사용하였다. 특히 vectorStringToString()에서 범위 기반 반복문을 사용함에 따라 간결성을 높일 수 있었다.
일관적이고 명료한 명명법: flipUpDown(), vectorStringToString() 등 이름을 간결하고 명확하게 짓고자 노력했다.

딱히 사용된게 많이 없는듯? 하지만 정말로 어려웠던 지점은...

2-6 회고

2-6-1 분할 정복이 나오게 된 배경

분할 정복은 재귀 다음에 나오는 테마로, 이 배경을 이해하면 어떤 문제가 분할 정복으로서 풀릴 수 있는지 구분하게 된다.

재귀 함수의 한계

우선 우리는 재귀를 배웠다. 여기서 들 예시는 1부터 n까지의 합 함수이다.

기존에 반복문으로써 하나하나 곱해나가는 것보다, 자기자신 함수를 호출함으로서 문제를 명료하게 풀 수 있다는... 그런 멋진 기법이다.

before

int toSumN(int n) {
	int res = 0;
	for (int i = 1; i <= n; ++i) {
    	res += i;
    }
    return i;
}

after

int toSumN(int n) {
	if (n == 1) return 1;
    return n + toSumN(n - 1);
}

하지만 이 기법은 한계가 있다. 바로 n이 1씩 줄어든다는 점이다. 선형적으로 값이 내려가기 때문에, 함수가 많이 호출된다는 느낌을 준다. 그럼 어떻게 하면 함수를 적게 호출할 수 있을까? 바로 반 씩 쪼개는 것이다.

분할 정복의 등장

반씩 쪼개며 호출하는 함수 fastSum()의 코드는 다음과 같다.

int fastSum(int n) 
{
	if(n == 1) return 1;
	if(n % 2 == 1) return fastSum(n-1) + n;
	return 2 * fastSum(n/2) + (n/2) * (n/2);
}

구현되는 원리와 수학적 배경은 이것을 참고한다. 무튼 뽀인트는 반으로 쪼갬으로써 로그 스케일로 문제를 해결할 수 있다는 것이다!

위에 fastSum()함수는 인자를 하나만 받는다. 하지만 이것은 수학 식이 예쁘게 정리되는 매우 특수한 경우이고, 대부분의 경우 탐색하고자 하는 범위를 인자로 주고 이 범위가 줄어듦을 관찰하는 경우가 대부분이다.

1. 분할 정복을 사용하므로써 로그 스케일로 문제를 해결할 수 있다.
2. 대부분의 경우 탐색하고자 하는 범위를 인자로 주고 이 범위가 줄어듦을 관찰한다.

2-6-2 while문은 언제 for문 대신 쓰이는가?

flipUpDown() 함수 내부를 보면 for문 대신 while문이 사용된 것을 확인할 수 있다. 코드가 길어지고 이해하는데에도 좀 더 걸리는 것 같다. 그럼에도 불구하고 while문을 써야하는 이유는 무엇일까?

바로 반복문을 제어하는 i값이 일정하게 늘어나지 않을 때 while문을 사용할 수 있다.

while문을 for문 대신 써야하는 경우: 반복문을 제어하는 변수가 일정하게 늘어나지 않을 때

예를 들어, 배열을 순회하는데 순회 간격이 달라질 때

flipUpDown() 함수에서는 주어진 문자열을 순회할 때 기본적으로 하나씩 보지만, 만약 x가 있다면 해당 사분면을 처리하고, 이 사분면을 다시 보면 안된다. 하지만 만약 하나씩 보며 순회를 하게 된다면 (for문을 사용하게 된다면) 이미 처리한 사분면을 다시금 관찰하게 된다.

예를 들어, xwb(xwwbw)b가 있다면, 가장 바깥 사분면 정보 벡터 quad는 3사분면으로 xbwww를 받게 된다. 이후 1씩 증가한다면 다음 4사분면을 위한 관찰은 b가 아닌 두 번째 x 다음의 w를 보게 된다. 따라서 문제가 있다!

이 지점을 깨닫는 것이 이번 문제를 해결하는 가장 중요했던 포인트였다.

2-6-3 디버깅하며 막힐 때

디버깅을 하다가 막히는 지점이 있다면,

작은 케이스부터 제대로 동작하는지 확인하자.

작성한 함수의 input, output, process를 재정의한다.

flipUpDown() 함수를 작성하던 중, 생각한대로 값이 잘 안 튀어나와서 머리를 싸맸다. 이때 내가 굉장히 어려운 테스트 케이스 xbwxwbbwb를 제일 먼저 시도하고 있다는 사실을 깨달았다. 얼마나 바보 같던지! 쉬운 것부터, 차근차근 해결한다는 마음으로... 작은 케이스부터 제대로 동작하는지 확인하자.

또, 작성한 함수의 input, output, process를 다시 생각해보는 것도 중요해보인다. flipUpDown() 함수를 작성하던 중 마지막 return문에서 'x' +를 붙이는 것을 처음에 깨닫지 못하여 헤맸다. 문자열을 받았고 뒤집힌 문자열을 출력해야 한다면, 'x' + 뒤집힌 사분면 정보를 반환하는 것이 응당 당연함을... 깨닫지 못했다.

3 구종만's Sol

3-1 구종만's 설계

가장 단순한 방법은

쿼드 트리 문자열 압축 풀기
풀고 뒤집기
뒤집은 결과를 쿼드 트리 문자열로 압축하기

일 것이다. 물론 메모리 초과 오류가 날 것이 자명하나, 문제를 푸는 아이디어르 떠올리기 위해 해당 함수를 구현해보자.

3-2 구종만's 구현

3-2-1 쿼드 트리 문자열 압축 풀기

char decompressed[MAX_SIZE][MAX_SIZE];
void decompress(const string &s, int y, int x, int size);

해당 함수는 s를 압축 해제하여 decompressed[y..y+size-1][x..x+size-1] 구간에 쓴다.

구현을 하다 보면, s의 나머지 부분을 넷으로 쪼개기가 까다롭다는 사실을 깨닫게 된다. 그도 그럴 것이, 각 부분의 길이가 일정하지 않다.

이를 해결하는 첫 번째 방법은 위치가 주어졌을 때 그 위치에서 시작하는 압축 결과의 길이를 반환하는 함수 getChunkLength()를 만드는 것이다. 하지만 이를 만들게 되면 비슷한 일을 하는 두 개의 함수를 각각 작성하게 되므로, 마음에 들지 않는다. (호출 스택이 많아지는 것 역시 구현이 꺼려지는 이유 중 하나이다.)

이를 해결하는 두 번째 방법은 유용하게 써먹을 수 있는 패턴인데, s를 미리 쪼개는 것이 아니라 decompress() 함수에서 필요한 만큼 가져다 쓰도록 하는 것이다. 그 방법은

decompress() 함수에 s를 통째로 전달하는 것이 아니라, s의 한 글자를 가리키는 포인터를 레퍼런스로 전달한다.
함수 내에서 한 글자를 검사할 때마다 이 포인터를 앞으로 한 칸씩 옮긴다.
검사 결과 x로 시작하지 않으면 단일하다는 뜻이므로 모두 해당 글자로 덮고, x면 1사분면 2사분면 3사분면 4사분면을 모두 호출하며 덮는다.

이때 반복자가 참조형으로 전달되기 때문에 재귀 호출 내부에서 반복자를 옮기면 밖에도 그 변화가 전달된다. 따라서 decompress() 함수가 종료되고 나면 반복자는 항상 다음 부분의 시작 위치를 가리키게 된다.

인 것이다! 길이가 일정하지 않은 부분을 순회해야 할 때 유용한 테크닉이다.

char decompressed[MAX_SIZE][MAX_SIZE];
void decompress(const string &s, int y, int x, int size) {
	char head = *(it++);
    if (head == 'b' || head == 'w') {
    	for (int dy = 0; dy < size; ++dy) {
        	for (int dx = 0; dx < size; ++dx) {
            	decompressed[y+dy][x+dx] = head;
            }
        }
    } else {
    	int half = size/2;
        decompress(it, y, x, half);
        decompress(it, y, x+half, half);
        decompress(it, y+half, x, half);
        decompress(it, y+half, x+half, half);
    }
}

3-2-2 쿼드 트리 문자열 압축 풀지 않고 바로 정답 내기

생각을 여기까지 전개했다면, 굳이 2차원 배열을 만들 필요가 없다는 사실을 알게 된다. 바로 주어진 문자열의 뒤집힌 문자열을 바로 반환하는 함수를 작성하는 것이다.

string reverse (string::iterator& it) {
	char head = *it;
    ++it;
    if (head == 'b' || head == 'w') return string(1, head);
    
    string upperLeft = reverse(it);
    string upperRight = reverse(it);
    string lowerLeft = reverse(it);
    string lowerRight = reverse(it);
    
    return string("x") + lowerLeft + lowerRight + upperLeft + upperRight;
}

이로써 문제를 해결할 수 있다! 포인터 레퍼런스를 전달하는 아이디어는 정말 멋진 아이디어이다...

3-3 구종만's 분석

reverse() 함수는 한 번 호출될 때마다 주어진 문자열의 한 글자씩을 사용한다. 따라서 함수가 호출되는 횟수는 문자열의 길이에 비례하므로 O(n)의 시간복잡도를 가진다. 따라서 시간 안에 충분히 해결할 수 있다.

3-4 구종만's Sol을 읽고 또 회고

3-4-1 관찰하고자 하는 요소의 길이가 달라질 때: 포인터 레퍼런스 전달 테크닉

관찰하고자 하는 요소의 길이가 계속 달라진다면, 포인터 레퍼런스를 전달함으로써 코드를 설계할 수 있다. 이것은 요소의 묶음을 그냥 쪼개는 것이 어려움으로, 함수가 필요한 만큼 가져다가 쓰도록 하는 기법이다. 설명은 아까 읽었던 글을 참고한다.

관찰하고자 하는 요소의 길이가 달라질 때: 포인터 레퍼런스 전달
1. 함수에 s의 한 글자를 가리키는 포인터를 레퍼런스로 전달한다.
2. 함수 내에서 한 글자를 검사할 때마다 이 포인터를 앞으로 한 칸씩 옮긴다.
3. 검사 결과에 따라 다른 액션을 취한다. return을 하던가, 아니면 재귀를 하던가!

4 끝

종만: "한 번 푼 문제를 다시 본다고 해서 배우는 것이 있을까 생각할 수도 있지만, 오히려 문제를 한 번만 풀어서는 그 문제에서 배울 수 있는 것들을 다 배우지 못하는 경우가 더 많습니다."

젠장... 아직도 써야하는 글이 2개나 남았다... 다음 글은 FENCE 문제와 FANMEETING 문제이다. 다음 글에서 만나요~ 안녕~

Daniel Oh

안녕하세요. 오도열입니다.

이전 포스트

[알고리즘 문제 해결 전략] 06.8 문제: 시계 맞추기 (문제 ID: CLOCKSYNC)

다음 포스트

[알고리즘 문제 해결 전략] 07.2 문제: 쿼드 트리 뒤집기 (문제 ID: QUADTREE)