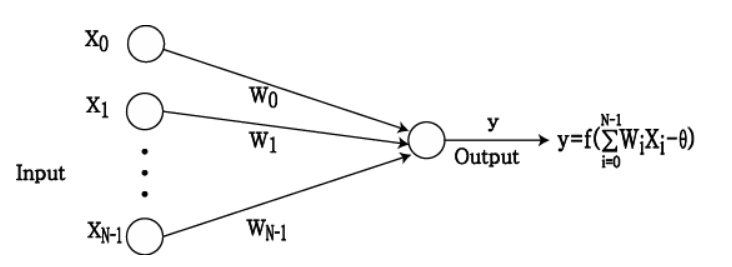
활성화 함수 (Activation Fuc)

뉴런이 입력 데이터를 처리하는 과정

• x인 입력 데이터는 가중치와 곱해진다. (x가 둘 이상일 경우 각 x에 서로 다른 가중치 w가 곱해진다.)
• 가중치와 데이터의 곱을 모두 더해준 후 활성화 함수에 대입된다.

활성화 함수에는 계단함수, 시그모이드, 하이퍼볼릭 탄젠트... 등이 있으며 활성화 함수를 거쳐 비선형적인 출력값을 갖는다.

여담으로
활성화 함수가 선형 Linear일 경우
활성화 함수는 f(z) = kz => f(wx+b) = k(wx+b)
그 다음 층 활성화 함수도 선형일 경우 f(z) = nz => n(k(wx+b))
입력 데이터에 상수를 곱해준 결과가 된다.
즉, 아무리 층을 쌓아도 층 하나와 같은 결과!
그래서 여러 층을 쌓는 딥러닝에서 선형 활성화 함수를 연속적으로 쓰지 않는다.

계단 함수는 퍼셉트론에 사용했던 활성화 함수인데 0과 1을 구분하는 이진 계산에 사용되었고 요즘은 안쓰이기 때문에 아래 그림만 보고 넘어가자~

1. sigmoid

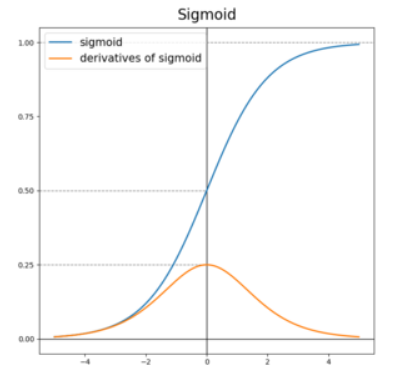
출력 결과가 0과 1 사이의 값으로 sigmoid 활성화 함수는 주로 2가지 경우를 분류할 때 쓰인다.

딥러닝 은닉층에서 sigmoid를 사용하지 않는데 이유는 기울기 소실(vanishing gradient)때문이다.
기울기 소실은 층을 많이 쌓았을 때 역전파를 하면 발생한다. 신경망은 정답과 예측을 비교하여 최적화할 때 역전파 미분을 하게 되는 데 시그모이드 함수는 여러번 미분할 경우 빠르게 0으로 가버린다. 위 그림 보면 시그모이드의 미분값은 0.25로 여러번 곱하면 작아지고 0에 가까워지는 걸 볼 수 있다. 결국 역전파가 뒤에서 앞으로 전달될 때 제대로 update가 되지 않아 학습이 느려지게 된다.

2. Tanh

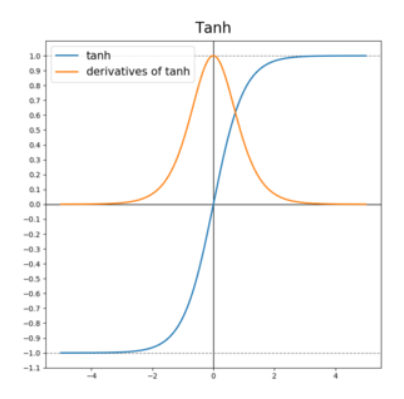
하이퍼볼릭 탄젠트이다. 시그모이드의 문제점을 보완하기위해 고안된 활성화 함수이다.
-1 과 1 사이의 값을 가지며 평균이 0이다.
미분했을 때 0과 1 사이 값을 가지며 폭이 넓어진 것을 볼 수 있다. 그래서 시그모이드 활성화 함수보다는 기울기 소실이 적은 편으로 은닉층에서 시그모이드 보다는 많이 쓰인다.

3. ReLU

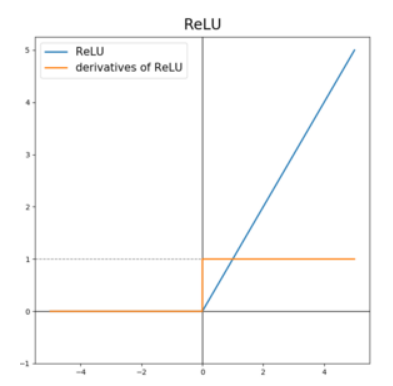
x>0 이면 기울기가 1인 직선이고, x<0이면 함수값이 0이된다.

sigmoid, tanh 함수와 비교했을 때 연산 비용이 크지 않기 때문에 학습이 훨씬 빠르다.

딥러닝 은닉층에 대부분 ReLU를 사용한다. 다른 활성화 함수에 비해 기울기 소실의 위험성이 적고 빠른 연산으로 학습이 빠르기 때문.

x<0인 값들에 대해서는 기울기가 0이기 때문에 뉴런이 죽을 수 있는 단점이 존재한다. (dying ReLU)

• ReLU의 문제는 모델이 학습하는 동안 일부 뉴런이 0만을 출력하여 활성화 되지 않는 문제
• 학습이 진행되면서 뉴런의 가중치가 업데이트 되면서 가중치 합이 음수가 되는 순간 ReLU에 의해 그 이후로는 0만 출력

4.Leaky ReLU

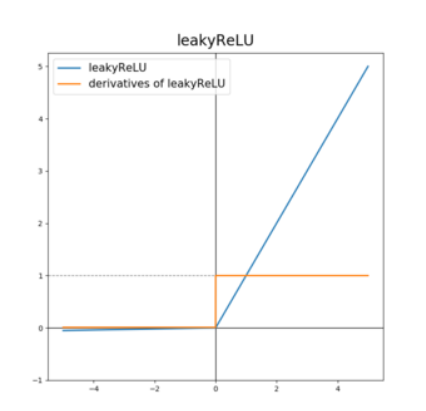
leakly ReLU는 ReLU의 뉴런이 죽는(“Dying ReLu”)현상을 해결하기위해 나온 함수이다.

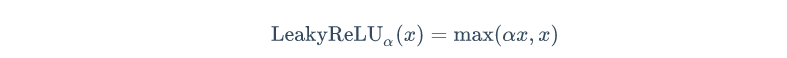
Leakly ReLU는 음수의 xx값에 대해 미분값이 0되지 않는다는 점을 제외하면 ReLU와 같은 특성을 가진다.

하이퍼파라미터인 a가 LeakyReLU함수의 새는(leaky, 기울기)정도를 결정하며, 일반적으로 0.01로 설정한다.
즉, 0 이하인 입력에 대해 활성화 함수가 0만을 출력하기 보다는 입력값에 a만큼 곱해진 값을 출력으로 내보내어 dead ReLU문제를 보완하였다.