베이즈 에러 Bayes Error

베이즈 에러는 이론적으로 도달 가능한 최소 오차입니다. 현실적으로 도달 가능한 최소 오차와는 다른 개념입니다. 그래서 머신러닝에서는 주어진 데이터로 도달 가능한 최소 오차 $E_{model}$과 $E_{Bayes}$ 간의 차이를 줄이는 것을 목표로 합니다.

'이론적으로 도달 가능한 최소 오차'라는 것은 실제 확률분포를 안다는 전제가 깔려 있습니다. 하지만 현실에서는 실제 확률분포를 알 수 없습니다. 그래서 일반적으로 상/하한을 계산하거나 도메인 지식을 통해 추정합니다.

Nearest Neighbor Classification

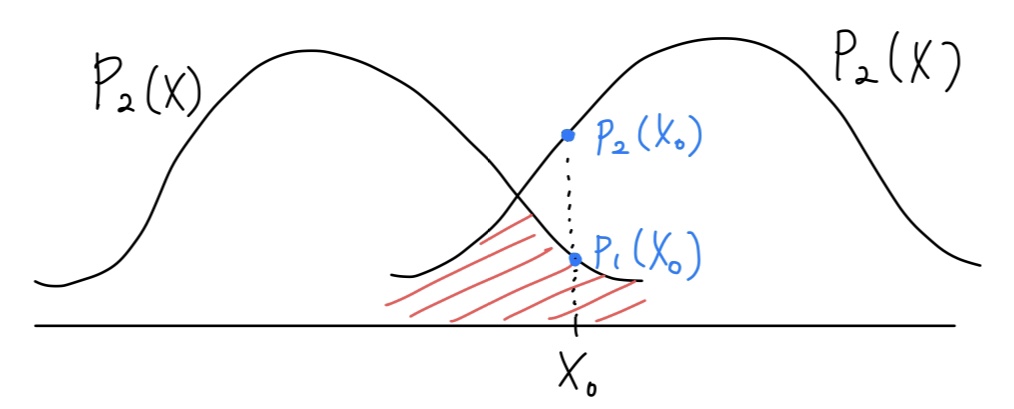
예를 들어 위와 같이 $P_1, P_2$ 2개의 분포가 주어졌다고 가정합시다. 각각의 확률분포 $P_n$은 $n$번째 클래스의 확률분포를 나타냅니다. 임의의 데이터 $x_0$이 주어졌을 때, 이 데이터의 클래스 $y(x_0)$를 분류하는 가장 합리적인(optimal) 방법은 다음과 같습니다.

위 그림에 따르면 $p_2(x_0)>p_1(x_0)$이므로 $y(x_0)=2$입니다.

그런데 실제로는 $y(x_0)=1$이었다면 어떨까요? $y$는 확률에 의존하기 때문에 충분히 이런 일도 발생할 수 있습니다. 이 경우 $x_0$에 대한 정밀도(precision)는 다음과 같이 나타낼 수 있습니다.

마찬가지로 분류기의 전체 정밀도는 다음과 같이 나타낼 수 있습니다.

오차를 최소화하려면 정밀도를 최대화하면 됩니다. 식 (1)에서 각각의 정밀도를 최대한 높게 만들어 주려면 두 확률분포가 겹치는 구간을 최대한 줄여야 합니다. 즉, 위 그림에서 색칠된 부분을 최소화하는 것과 같습니다. 이를 식으로 나타내면 다음과 같습니다.

$p_1+p_2=1$이고, $p(x)={p_1(x)+p_2(x)\over2}$이므로 식 (2)를 아래와 같이 나타낼 수 있습니다.

기하학적 관점

위 그림에서 개별 점은 각각의 데이터 포인트이고, $x'$는 모델이 $x$에 대해 예측한 값입니다. 모델이 Consistent Learner라면, 모델의 출력 $x'$가 실제 데이터 $x$에 가까울수록 모델의 정확도는 높아지고 오차는 줄어들 것입니다.

이 때 모델의 에러율은 다음과 같습니다.

만약 모델을 잘 구축했고, 무수히 많은 데이터가 존재한다면 식 (4)는 다음과 같이 수렴할 것입니다.

식 (5)의 기댓값을 구하면 그게 바로 베이즈 에러의 하한이 됩니다.