[선형대수] 기초 개념 정리

스칼라와 벡터

스칼라

• 상수라고 생각하면 된다. 보통 소문자 $s$의 형태로 표기한다.

벡터

• 1) 크기와 방향을 가진 값. 기하학적인 관점.
• 2) 나열된 숫자의 리스트. 하나의 데이터 값으로 생각하면 된다.

벡터는 소문자 $a, b, u, v$ 등으로 표기하거나 $\vec{a}, \vec{b}$ 등으로 표기한다.

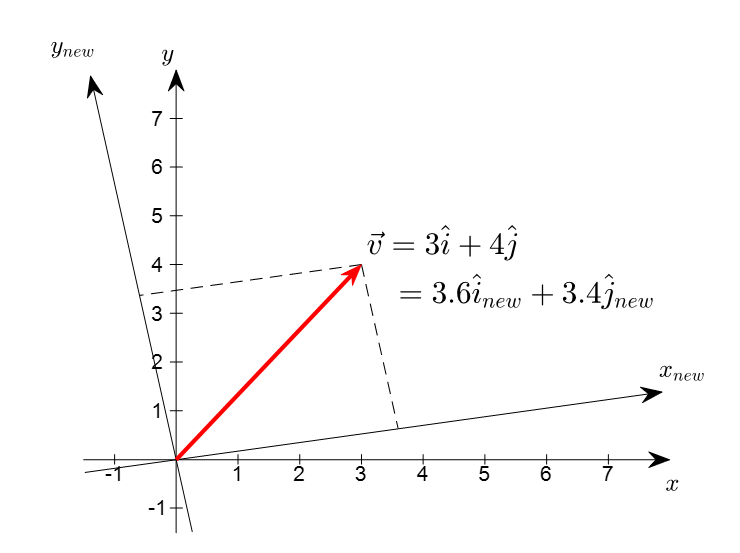
(출처: https://angeloyeo.github.io/2020/09/07/basic_vector_operation.html)

벡터는 위 두 정의 중 어느 것으로 바라보느냐에 따라 헷갈리기 쉽다.

좌표계가 바뀌어도 벡터는 그대로지만 (=불변성, invariance)
좌표계가 바뀌면 벡터의 성분은 바뀐다. (=가변적, variant)

열벡터

• 행렬의 열을 벡터로 보는 관점.
  행렬은 기본적으로 열벡터를 기준으로 표기한다.
  

행벡터

• 행렬의 행을 벡터로 보는 관점.
  열벡터를 행벡터로 표기할 때는 전치행렬처럼 $A^T$와 같이 표기한다.
  

$A = \begin{bmatrix} 1 & 2 & 3 & 4\\ \end{bmatrix}, A^T = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}$

---

행렬과 벡터의 계산

행렬의 표기

• $A \in \mathbb{R}^{m \times n}$ 와 같이 표기한다. $m$은 행, $n$은 열이다.
• $A_{ij}$ 는 $i$번째 행의 $j$번째 열에 있는 원소이고, $A_{,j}$는 $j$번째 열벡터, $A_{i,}$는 $i$번째 행벡터이다.

행렬의 덧셈과 곱셈

• 행렬 $A, B$에 대해 $A+B$는 각 원소끼리 덧셈
• 스칼라 $c$에 대해 $cA, ca$는 각 행렬 또는 벡터의 각 원소(성분)에 바로 곱셈

행렬곱

• 행렬 $A, B$에 대해 $C=AB$ 형태로 표기한다.
• 교환법칙이 성립하지 않는다.
• 결합법칙, 분배법칙은 성립한다.
• $C_{ij} = \sum_kA_{i,k}B_{k,j}$
• $(AB)^T = B^TA^T$, $(AB)^{-1} = B^{-1}A^{-1}$이 성립한다.

---

내적과 외적

내적과 외적은 서로 상관없는 연산이며,

외적은 벡터곱(cross product)과 선형대수학에서 사용하는 텐서곱(outer product)
2가지 종류가 있어서 헷갈리기 쉽다.

내적(dot product)

• 내적은 두 벡터의 각 성분끼리 곱한 것의 합이다.

• $x \cdot y$ 형태로 표기하며, 결과값은 스칼라이다.

• 교환법칙이 성립한다.

• $x \cdot y = \lVert a \rVert \lVert b \rVert\cos\theta$ 이다.

• 두 벡터의 내적값으로 두 벡터가 얼마나 같은 방향을 향하는지 (=유사한지) 알 수 있다.

$(1, n)$ 벡터끼리의 내적은 $(1,n), (n,1)$ 행렬끼리의 행렬곱으로 표현할 수 있다.
즉, $u \cdot v = uv^T$가 성립하며, 결과값은 스칼라이다.

(예시) $\begin{bmatrix} 1 \\ 2 \end{bmatrix} [2 \quad 3] = 1*2 +2*3 = 8$

즉, 행렬의 각 원소는 재료벡터의 각 성분끼리의 내적값이다.
이 성질을 가지고 공분산행렬을 만들 수 있다.

벡터곱(cross product)

• 벡터곱은 두 벡터 $x, y$에 대해 서로 수직인 벡터를 구하는 연산이다.

• $x \times y$ 형태로 표기한다.

• 교환법칙이 성립하지 않는다.

• $x \times y$의 크기는 $\left\vert a \right\vert\left\vert b \right\vert\sin\theta$이고, 결과값은 벡터이다. ($\theta$는 두 벡터가 이루는 각의 크기)

• $x = [x_1, x_2, x_3], y = [y_1, y_2, y_3]$일 때, $x \times y = [x_2y_3-x_3y_2, x_3y_1-x_1y_3, x_1y_2-x_2y_1]$이다.

자세히 보면 벡터곱의 각 성분은 행렬식(판별식) $det = ad-bc$와 같다는 것을 알 수 있다.
행렬식이 0이면 해가 없거나 무수히 많고, 0이 아니면 반드시 단 하나의 해가 존재한다.

이러한 성질을 여러 가지 방면으로 활용할 수 있다.
예를 들어 두 3차원 벡터의 벡터곱이 영벡터라면 두 벡터는 평행하다.

텐서곱(outer product)

• 텐서곱은 두 벡터의 행렬곱 연산이다.

• $u \bigodot v$ 형태로 표기한다.

• 교환법칙이 성립하지 않는다. (결합법칙은 성립함)

• $u \bigodot v = uv^T$이며, 결과값은 행렬이다.
  내적과 동일한 행렬곱 형태로 표현할 수 있지만 행렬의 모양이 다르다는 것을 기억하자.
  $u=(4,1), v=(4,1)$ 모양의 벡터라면 텐서곱 결과는 $(4,4)$의 모양을 갖는 행렬이 된다.

• 텐서곱의 주대각합은 내적과 같다.

---

선형성의 의미

어떤 것이 선형이라는 것은 쉽게 말해 작은 조각들로 쪼갤 수 있다는 것이다.
바꿔 말하면 작은 조각들을 합쳐서 큰 조각을 만들 수도 있다는 의미가 된다.

선형의 수학적 정의는 다음과 같다.

동일한 체 $F$에서 정의된 벡터공간 $V, W$에 대해 정의된 함수 $T:V \rightarrow W$가 다음 두 조건을 만족하면 선형변환(Linear transformation) 또는 일차변환(First-order transformation)이라 정의한다.

1) 중첩의 원리 (superposition)
$T(x) + T(y) = T(x+y)$

2) 동질성 (homogenuous)
$c*T(x) = T(c*x)$

선형변환을 줄여서 간단하게 선형 또는 $L(V,W)$로 표기하기도 한다.

이게 신경망에서 무슨 역할을 하는지는 링크에 간단하게 설명돼 있다.

선형성의 성질

$T(V \rightarrow W)$가 선형이면 다음과 같은 성질을 갖는다.

1) 모든 $x, y \in V$에 대해 $T(cx+y) = c*T(x)+T(y)$
2) 모든 $x, y \in V$에 대해 $T(x-y) = T(x) - T(y)$
3) 모든 $x, y \in V$에 대해 $T(\mathbf{0})= \mathbf{0}$
4) $x_1, x_2, \cdots x_n \in V$ 와 $a_1, a_2, \cdots a_n \in F$에 대해 $T(\sum_{i=1}^n a_ix_i) = \sum_{i=1}^n a_iT(x_i)$

1번과 2번은 선형성의 정의와 같다.

3번을 직해하면 영벡터를 선형변환한 것은 영벡터라는 것인데,
쉽게 말해서 모든 선형함수는 반드시 원점을 지나야 한다는 의미가 된다.