[딥러닝] Layer Collaboration in the Forward-Forward Algorithm

Ethan·2023년 9월 13일
DLForward-Forwardff
0

Papers Review

목록 보기
14/19

요약

  • Original FF의 네트워크 구조를 엔트로피 관점에서 분석
    - FF는 레이어 간 소통이 원활하지 않아 정보량이 한정됨 (overfitting 위험 증가)
    - Representation의 diversity와 confidence간 trade off가 존재
  • θ,σ\theta, \sigma 등 불필요한 모듈 제거 →\rightarrow goodness function 경량화
    - 경량화 후에도 기존과 비슷한 성능을 보임

Background

Hinton이 발표한 Forward-Forward algorithm (FF)은 Back Propagation (BP)의 대체재로 새롭게 제시된 학습 방법입니다. 모듈 단위로 최적화를 진행하기 때문에 BP처럼 레이어에 대한 의존성 문제가 없고, feed forward network만으로 최적화가 가능하다는 장점이 있지만, 반대로 성능적 측면에서 아직 오차역전파보다 부족하고 레이어 수에 따라서는 오히려 메모리를 더 많이 사용할 수도 있습니다. 게다가 레이어 자체적으로 학습의 완결성을 가지기 때문에 다른 레이어들과 정보 교환(layer collaboration)이 원활하지 않다는 문제가 있습니다.

Original FF는 goodness라는 개념을 도입해서 각각의 레이어 최적화 정도를 판단하는데, 예를 들어 input data xx에 대해 네트워크를 구성하는 nn개의 레이어를 f1:nf_{1:n}라고 한다면 다음과 같이 나타낼 수 있습니다.

p(positive)=(1+e−(∑jnfj(x)2−θ))−1(1)p(\text{positive})=\left({1+e^{-(\sum _j^nf_j(x)^2-\theta)}}\right)^{-1}\qquad(1)

이 때 θ\theta는 goodness를 나타내는 스칼라 값으로, 이전 레이어에서 출력한 hidden vector의 L2 norm의 제곱 (∣∣f1:n(x,y)∣∣2)(||f_{1:n}(x,y)||^2) 입니다. FF는 이 goodness 값을 기준으로 레이어의 최적화 정도를 판단합니다. Positive sample에 대해 goodness 값이 크고, negative sample에 대해 goodness 값이 작을수록 레이어가 잘 최적화되었다고 보는 것이죠.

그런데 곰곰이 생각해보면 이건 조금 이상합니다.

'레이어 출력의 L2 norm의 제곱'이라는 건 그냥 벡터의 크기입니다. 즉, 벡터의 방향과 구성을 고려하지 않습니다. Positive sample에 대한 goodness가 크다고 해서 정말로 downstream task를 잘 수행할 수 있다는 보장도 없습니다.

게다가 다수의 레이어를 사용한다면 문제가 커집니다. Layer-wise하게 goodness를 최적화하면 레이어마다 목표가 달라지게 되는데, 각 레이어가 보는 데이터는 이미 이전 레이어에서 다른 관점으로 처리된 데이터이기 때문입니다.

예를 들어, 만약 1번 레이어에서 A라는 관점으로 최적화한 데이터를 넘겨받은 2번 레이어가 B라는 관점으로 데이터를 최적화하려고 해도, 이미 A의 관점에서 불필요한 정보를 제거했기 때문에 B의 관점에서 중요한 정보가 소실되었을 가능성이 있습니다.

다행인 점은, 저자들의 실험에 따르면 original FF는 여러 레이어를 거치면서 네트워크의 functional entropy가 증가하는 경향이 있었습니다. 네트워크의 엔트로피가 증가한다는 것은 hidden representation의 다양성이 증가했다는 것이고 이는 곧 네트워크가 여러 input을 잘 구분한다는 의미입니다.

그런데 레이어를 거치면서 점점 네트워크의 표현력이 증가한다는 게 항상 좋은 것은 아닙니다. 무의미한 노이즈가 증가해도 표현력은 증가하기 때문이죠. 즉, 네트워크의 엔트로피를 측정하는 것만으로는 모델이 정말로 유의미한 표현력을 가졌는지 확신할 수 없습니다.

그렇다면 어떻게 해야 할까요?

Methods

Layer collaboration

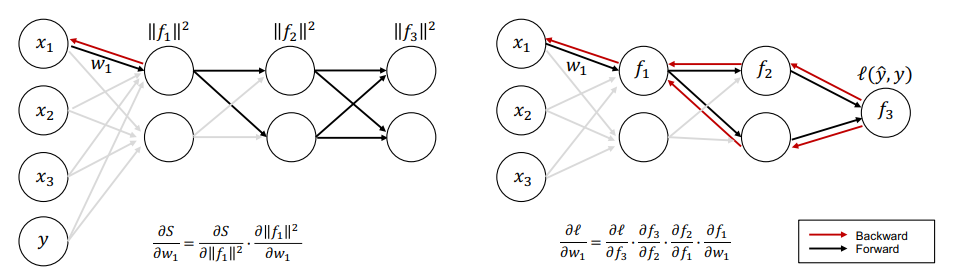
Forward-forward 알고리즘은 오직 forward pass로만 정보를 전달합니다. 왼쪽 그래프를 보면 앞쪽 레이어는 뒤쪽 레이어들에게서 정보를 받지 못하고 있지만, 오른쪽 오차역전파 그래프를 보면 선행 레이어들도 후행 레이어들에게서 정보를 넘겨받을 수 있습니다.

그래서 FF 알고리즘은 각 레이어의 goodness를 합산하는 방식을 사용합니다. 개별 레이어가 하나의 네트워크라고 보면 여러 네트워크의 판단을 총합하여 global goodness를 만들고, 이를 바탕으로 주어진 xx에 대해 가장 적합한 yy를 판단하는 것입니다. 일종의 voting이라고 할 수 있습니다.

이걸 수식으로 표현하면 다음과 같습니다.

pi(positive)=Δ(1+e−(∥f1:i(x,y)∥2+γ−θ))−1(3)p_i(\text{positive})\overset{\Delta}{=}\left(1+e^{-(\lVert f_{1:i}(x,y)\rVert^2+\gamma-\theta)}\right)^{-1}\qquad(3)

식 (3)을 Collaborative Forward-Forward 라고 합니다. Classic FF와 비교하면 학습 방향을 조정하기 위한 새로운 regularization term γ\gamma가 추가되었습니다. 이 때 γ\gamma 값은 다음과 같이 정합니다.

γ=∑t≠i∥f^1:t(x,y)∥2orγ<t=∑t<i∥f^1:t(x,y)∥2\gamma=\sum_{t\neq i}\lVert\hat{f}_{1:t}(x,y)\rVert^2\qquad \text{or}\qquad\gamma_{<t}=\sum_{t<i}\lVert\hat{f}_{1:t}(x,y)\rVert^2

즉, γ\gamma는 자신을 제외한 다른 레이어들의 정보입니다. (f^\hat{f}는 네트워크 ff의 copy)

결과적으로 Collaborative FF는 tt번째 레이어를 최적화하는 데 tt 이전까지의 레이어들의 goodness를 합산하거나, 혹은 아예 자신을 제외한 나머지 레이어들의 goodness를 합산해서 threshold θ\theta 값에 반영합니다.

Collaborative FF의 최적화 과정은 다음과 같이 나타낼 수 있습니다.

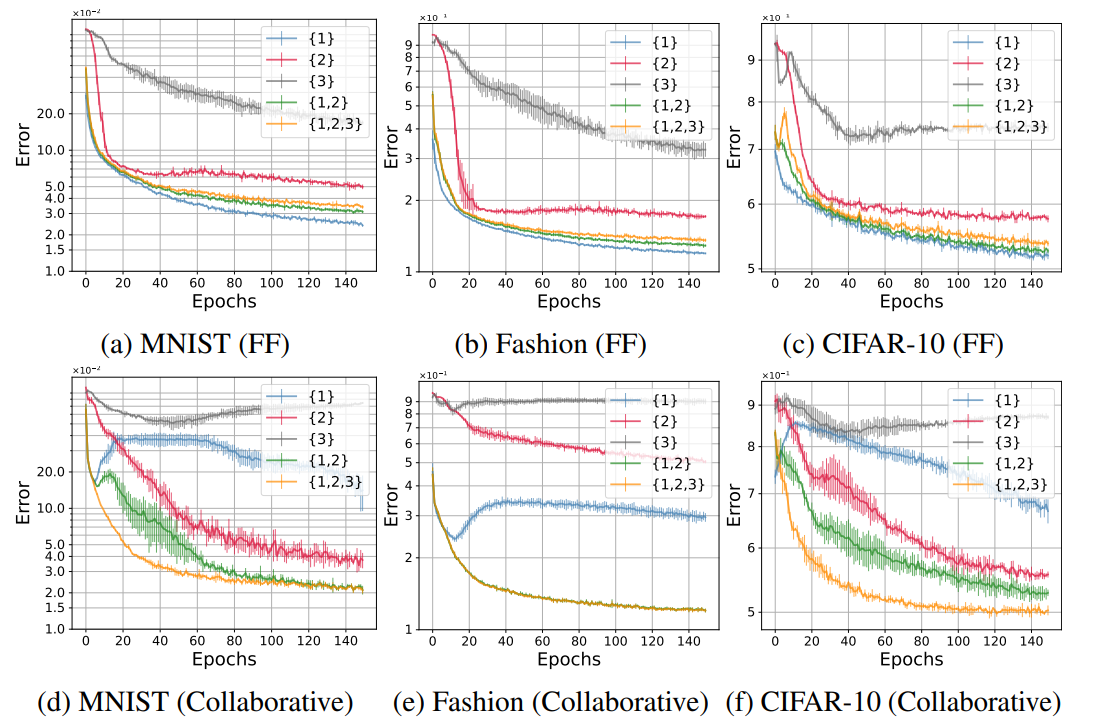
Δwi=∂log⁡((1+e−(∥f1:i(x,y)∥2+γ−θ))−1)∂wi\Delta w_i={\partial\log\left((1+e^{-(\lVert f_{1:i}(x,y)\rVert^2+\gamma-\theta)})^{-1}\right)\over\partial w_i}

위 그림은 레이어 조합에 따른 모델의 성능을 비교한 그래프입니다. 앞쪽에 위치한 레이어일수록 더 성능이 좋다는 걸 알 수 있습니다. Original FF에서는 여러 레이어를 사용할수록 성능이 조금씩 감소하는 반면, collaborative FF는 여러 레이어의 성능을 모두 고려하는 것이 가장 성능이 좋습니다.

기본적으로 딥러닝 네트워크는 선행 레이어의 출력에 의존하기 때문에 뒤쪽 레이어로 갈 수록 각 레이어가 고려할 수 있는 정보가 감소합니다. 대신 앞쪽 레이어에서 정보가 필터링되기 때문에 조금 더 질 좋은 정보를 받을 수 있게 되는데요. 만약 뒤쪽 레이어로 갈 수록 성능이 저하된다면 후속 레이어에서 필요한 정보가 충분히 전달되지 않고 있다는 것을 의미합니다.

이런 관점에서 볼 때 original FF에서 여러 레이어가 동일한 goodness function을 사용할 경우 뒤쪽 레이어의 존재 가치가 떨어지고, 서로 다른 goodness function을 사용하면 뒤쪽 레이어로 전달되는 정보의 quality control이 힘들어지는 문제가 발생할 수 있습니다.

ㅁㄴㅇㅁㅇ

γ\gamma가 추가된 것 외에도 학습 순서가 약간 변형되었는데, 먼저 original FF는 선행 레이어부터 학습을 진행하며 각각의 goodness를 최적화시킵니다. 즉, 1번 레이어 최적화가 완료된 이후에 2번, 3번, ... 순으로 학습이 진행됩니다.

반면 collaborative FF는 먼저 모든 레이어의 goodness를 계산하고, global goodness가 수렴할 때까지 학습을 반복합니다. 즉, 1→2→31\rightarrow2\rightarrow3 순으로 goodness를 계산하여 취합하고 이를 기준으로 최적화를 수행합니다.

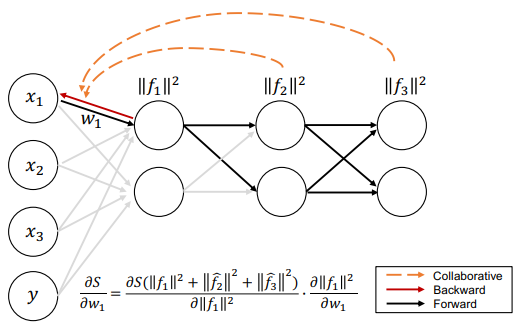
위 그림을 보면 layer 내에서 backward가 진행될 때마다 다른 레이어의 정보를 고려하여 최적화가 진행됩니다. 결과적으로 전체 dataset SS에 대한 가중치 w1w_1의 값은 모든 레이어의 goodness를 합산한 값을 해당 레이어의 goodness에 대해 미분한 값과 해당 레이어의 goodness를 가중치 w1w_1로 미분한 값의 곱이 됩니다. 즉, 전체 네트워크의 상태에 대한 해당 레이어의 기여도를 구할 수 있습니다.

Classic FF와 Collaborative FF 모두 개별적으로 최적화된 레이어들의 합으로 네트워크를 정의하는 것은 같지만, 전자는 단순히 최종 합만 높으면 되기 때문에 다른 레이어에 대해 none of my business인 반면 후자는 최종 합을 높이는 것에 더해 개별 레이어 간 최적의 파라미터 구성을 찾아내는 것이 목표가 됩니다. 그 과정에서 전자에 비해 overfitting을 완화하게 될 것이란 기대도 해볼 수 있습니다.

한 편, 이 부분에서 몇 가지 의문점도 생깁니다.

  • Collaborative FF는 오차역전파 대비 충분한 메모리 이득이 있는가?
    오차역전파가 메모리를 많이 사용하는 이유는 계산을 하기 위해 네트워크 전체를 메모리에 올려야 할 필요가 있기 때문입니다. 물론 Collaborative FF는 가중치 전체를 몰라도 개별 goodness 값만 알면 되기 때문에 조금 더 경량화시킬 순 있겠지만, 메모리 활용 측면에서 충분한 이득이 되지 않는다면 굳이 성능적 우위를 버리고 FF 계열 알고리즘으로 갈아탈 이유가 없겠죠.
  • 레이어의 목적함수를 유기적으로 선택할 수 있는가?
    예를 들어 1번 레이어는 MSE를 사용하지만, 2번 레이어는 MAE를 사용한다고 가정해봅시다. Original FF에서 개별 레이어의 최적화는 타 레이어의 최적화와 별로 상관이 없기 때문에 두 레이어의 목적함수가 반드시 같을 필요가 없습니다. 하지만 Collaborative FF는 각각의 레이어들의 goodness가 유기적으로 global goodness를 구성하기 때문에 개별 레이어의 목적함수에 큰 영향을 받을 가능성이 높습니다. 그렇다면 서로 다른 역할의 모듈을 유기적으로 연결했을 때 성능 저하가 발생하지 않을까요?

Entropic view of layer collaboration

여기서부터 흥미로운 부분입니다.

Probability measure μ(z)\mu(z)를 갖는 공간 Z\mathcal{Z}에서 정의되는 임의의 함수 h(z)h(z)가 있다고 가정해 보겠습니다. h(z)h(z)는 레이어를 나타내는 함수이고, h(z)≥0h(z)\geq0의 functional entropy는 다음과 같습니다.

Entμ(h)=ΔEz∼μ[h(z)log⁡(h(z))Ez∼μ[h(z)]](4)\text{Ent}_\mu(h)\overset{\Delta}{=}\mathbb{E}_{z\sim\mu}\left[h(z)\log(h(z))\over \mathbb{E}_{z\sim\mu}[h(z)]\right]\qquad(4)

분모에 Ez∼μ[h(z)]\mathbb{E}_{z\sim\mu}[h(z)]가 붙는 이유는 엔트로피의 정의에 맞게 scaling을 해주기 위해서입니다. 만약 h(z)h(z)가 상수라면 식 (4)의 값은 0이 되겠죠.

여기서 layer h(z)=Δ∥f1:i(x,y)∥2h(z)\overset{\Delta}{=}\lVert f_{1:i}(x,y)\rVert^2의 prior를 p(z)p(z), posterior를 q(z)q(z)라고 하면 다음과 같습니다. 여기서 prior는 데이터의 분포를 의미하고, posterior는 레이어가 근사한 분포를 가리킵니다. Representation이라고 봐도 됩니다.

p(z)=Δdμ(z),q(z)=Δp(z)h(z)Ez∼μ[h(z)]p(z)\overset{\Delta}{=}d\mu(z),\qquad q(z)\overset{\Delta}{=}{p(z)h(z)\over \mathbb{E}_{z\sim\mu}[h(z)]}

q(z)≥0q(z)\geq0 이고 Ez∼μ[q(z)]=1\mathbb{E}_{z\sim\mu}[q(z)]=1 이므로 q(z)q(z)를 확률분포로 해석할 수 있습니다. 결과적으로 식 (4)를 layer의 prior & posterior간의 scaled KL Divergence로 해석할 수 있습니다.

Entz∼μ(h)=Ez∼μ[h(z)]⋅KL(q∣∣p)(5)\text{Ent}_{z\sim\mu}(h)=\mathbb{E}_{z\sim\mu}[h(z)]\cdot KL(q||p)\qquad(5)

식 (5)의 우변을 보면 해당 레이어의 엔트로피는 p(z)p(z)와 q(z)q(z) 간의 KL Divergence 값에 따라 scaling 됩니다. 즉, KL Divergence 항을 레이어의 학습량에 대한 지표로 해석할 수 있습니다.

Forward-Forward 알고리즘을 사용해서 contrastive learning을 하는 예시를 생각해봅시다. 순전파에 해당하는 positive forward 시에는 레이어가 prior를 근사하는 방향으로 학습이 진행되므로 KL divergence가 감소합니다. 반대로 negative forward 시에는 레이어가 prior에서 멀어지려고 하므로 KL divergence가 증가하게 됩니다. 즉, positive pass에서는 positive representation Entpos(h)\text{Ent}_{pos}(h)에 대한 엔트로피가 작아지고 negative pass에서는 negative representation Entneg(h)\text{Ent}_{neg}(h)에 대한 엔트로피가 커지게 되겠죠.

그런데 잘 생각해보면 negative sample에 대해 네트워크의 엔트로피가 커져서 별로 좋을 것이 없습니다. Negative representation의 엔트로피가 커진다는 것은 representation space 상에서 negative로 취급되는 영역이 넓어지는 것과 같은 의미로, positive region이 감소하는 것과 같습니다. 즉, contrastive learning과 마찬가지로 regularization term으로 작용한다는 뜻인데 FF 알고리즘은 레이어간 정보 교환이 거의 일어나지 않습니다. 쉽게 말해서 주어진 정보량은 한정돼 있는데 regularization이 과도한 상황인 것이죠. 당연히 overfitting이 일어나기 매우 쉬운 상태가 됩니다.

그렇다고 해서 positive sample에 대해서 엔트로피가 감소하는 것도 마냥 좋지만은 않습니다. 당연하지만 shortcut을 학습해버려 overfitting이 발생할 위험이 증가하기 때문입니다. 따라서 KL divergence 값을 감소시키되, 완벽하게 input의 분포를 모사하기보다는 중요한 정보를 중심으로 추출하는 것이 핵심입니다. (이와 관련하여 유명한 선행 연구가 있습니다.)

여기서 레이어간 정보를 원활하게 전달할 수 있는 Collaborative FF를 사용한다면 negative sample이 지나치게 제약으로 작용하는 상황을 방지할 수 있으므로 overfitting이 상대적으로 완화됩니다.

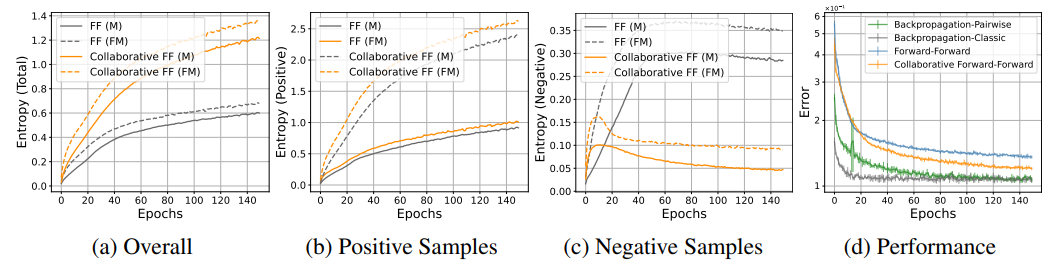
실제로 실험 결과를 보면 negative sample에 대한 엔트로피가 original FF보다 훨씬 빠른 속도로 감소합니다. 반대로 positive sample에 대한 엔트로피는 증가하였는데 이는 각 레이어가 고려하는 정보량이 증가하여 representation space에서 positive / negative region의 상대적 균형이 어느 정도 보정되었다는 것을 의미합니다.

Entropy-based optimization

저자들은 original FF가 내부의 functional entropy를 최대화하려는 경향이 있다는 점에 착안하여 maximize entropy optimization을 시도하였습니다. 수식으로 나타내면 다음과 같습니다.

Entμ2[h(⋅,⋅,i)]=E[h(x,y,i)log⁡(h(x,y,i)E[h(x,y,i)])]\text{Ent}_{\mu_2}[h(\cdot,\cdot,i)]=\mathbb{E}\left[h(x,y,i)\log\left({h(x,y,i)\over\mathbb{E}[h(x,y,i)]}\right)\right]

복잡해 보이지만 그냥 ii번째 레이어에 대해 식 (4)를 maximize한 것입니다.

성능적으로는 기존의 최적화 방법과 큰 차이가 없었지만 (FashionMNIST 기준 original FF 대비 -0.1%, Collaborative FF 대비 -0.9%), 원래 방법과 비교하여 별도의 θ\theta 값이 필요 없고 sigmoid function도 사용하지 않는다는 장점이 있습니다.

Limitations

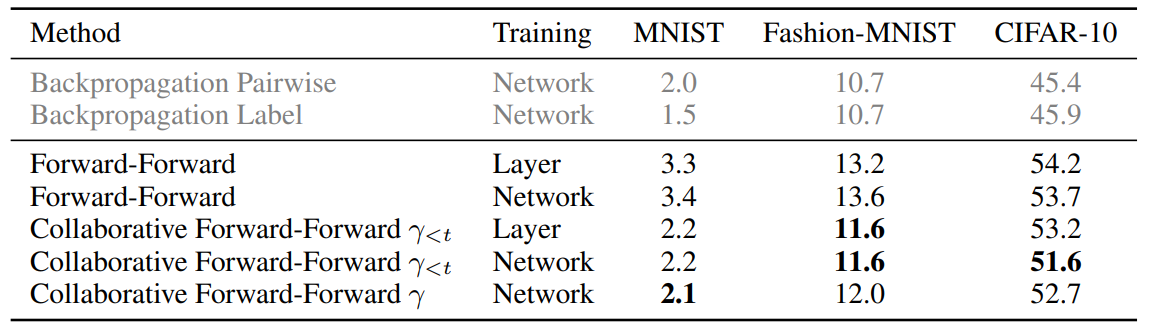
Layer는 개별 레이어를 먼저 최적화시킨 것이고, Network는 전체 네트워크를 동시에 최적화시킨 것입니다. Collaborative FF의 최고 성능과 오차역전파의 최저 성능을 비교해 봤을 때, MNIST는 -5%, Fashion-MNIST는 -8.4%, CIFAR-10에서는 -12.4%로 여전히 큰 성능적 격차가 존재합니다.

profile
Ethan
재미있게 살고 싶은 대학원생
이전 포스트

[NLP] Attention Is All You Need (Transformer)

다음 포스트

[딥러닝] Bootstrap Your Own Latent : A New Approach to Self-Supervised Learning (BYOL)

0개의 댓글