
너비 우선 탐색도 그래프를 완전 탐색하는 방법 중 하나로, 시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘
그래프 완전 탐색
- FIFO 탐색
- Queue 자료구조 이용
시간 복잡도 ( 노드 수 : V, 에지 수 : E ) : O(V+E)
선입선출 방식으로 탐색하므로 큐를 이용해 구현, 또한 탐색 시작 노드와 가까운 노드를 우선하여 탐색하므로 목표 노드에 도착하는 경로가 여러 개일 때 최단 경로를 보장한다.
-
BFS를 시작할 노드를 정한 후 사용할 자료구조 초기화 하기
방문했떤 노드는 다시 방문하지 않으므로 방문할 노드를 체크하기 위한 배열이 필요하다. 스택이 아닌 큐를 사용한다 -
큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입
큐에서 노드를 꺼내면서 인접 노드를 큐에 삽입한다. 이때 방문 배열을 체크하여 이미 방문한 노드는 큐에 삽입하지 않는다. 또한 큐에서 꺼낸 노드는 탐색 순서에 기록한다. -
큐 자료구조에 값이 없을 때까지 반복한다
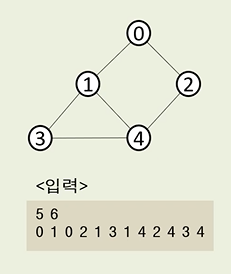
public class Main {
static final int MAX_N = 10;
static int N,E;
static int[][] Graph = new int[MAX_N][MAX_N];
static void bfs(int node) {
boolean[] visited = new boolean[MAX_N];
Queue<Integer> myqueue = new LinkedList<>();
visited[node] = true; // 방문한 노드 재방문 안하기위해 마킹
myqueue.add(node);
while(!myqueue.isEmpty()) {
int curr = myqueue.remove();
System.out.print(curr+" ");
for(int next = 0; next < N; next++) {
if(!visited[next]&&Graph[curr][next] != 0) {
visited[next] = true;
myqueue.add(next);
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
E = sc.nextInt();
for(int i=0; i<E; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
Graph[u][v] = Graph[v][u] = 1; // 방향성이 없다는걸 의미
}
bfs(0);
}
} //0 1 2 3 4 
// 최단경로 구하기
public class Main {
static final int MAX_N = 10;
static int[][] D = {{-1,0},{1,0},{0,-1},{0,1}};
static int N;
static int[][] Board = new int[MAX_N][MAX_N];
static class Point {
Point(int r,int c, int d) {
row=r; col=c; dist=d;
}
int row,col,dist;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
Board[i][j] = sc.nextInt();
int sRow,sCol,dRow,dCol;
sRow = sc.nextInt(); sCol=sc.nextInt();
dRow=sc.nextInt(); dCol=sc.nextInt();
System.out.println(bfs(sRow,sCol,dRow,dCol));
}
static int bfs(int sRow, int sCol, int dRow, int dCol) {
boolean[][] visited = new boolean[MAX_N][MAX_N];
Queue<Point> myqueue = new LinkedList<>();
visited[sRow][sCol]=true;
myqueue.add(new Point(sRow,sCol,0));
while(!myqueue.isEmpty()) {
Point curr = myqueue.remove();
if(curr.row == dRow && curr.col == dCol)
return curr.dist;
for(int i=0; i<4; i++) {
int nr = curr.row + D[i][0], nc = curr.col + D[i][1];
if(nr < 0 || nr > N-1 || nc < 0 || nc > N-1) continue;
if(visited[nr][nc]) continue;
if(Board[nr][nc]==1) continue;
visited[nr][nc] = true;
myqueue.add(new Point(nr,nc,curr.dist + 1));
}
}
return -1;
}
} // 11// 파이썬
from collections import deque
# BFS 메서드 정의
def bfs(graph,start,visited):
# Queue 구현을 위해 deque 라이브러리 사용
queue = deque([start])
# 현재 노드를 방문 처리
visited[start] = true
# 큐가 빌 때 까지 반복
while queue:
# 큐에서 하나의 원소를 뽑아 출력하기
v = queue.popleft()
print(v,end=' ')
# 아직 방문하기 않은 인접한 원소들을 큐에 삽입
for i in graph[v]:
if not visited[i]:
queue,append(i)
visited[i] = True
# 각 노드가 연결된 정보를 표현(2차원 리스트)
graph = [
[],
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
# 각 노드가 방문된 정보를 표현(1차원 리스트)
visited = [False]*9
# 정의된 BFS 함수 호출
bfs(graph, 1, visited)
// 1 2 3 8 7 4 5 6N X M 크기의 얼음 틀이 있다. 구멍이 뚫려 있는 부분은 0, 칸막이가 존재하는 부분은 1로 표시한다. 구멍이 뚫려 있는 부분끼리 상,하,좌,우로 붙어있는 경우 서로 연결되어 있는것으로 간주한다. 이때 얼음 틀의 모양이 주어졌을 떄 생성되는 총 아이크스림의 개수를 구하는 프로그램을 작성.
4 5
00110
00011
11111
00000 // 3
이 문제는 DFS 혹은 BFS로 해결할 수 있다
DFS를 활용하는 알고리즘은 다음과 같다
1. 특정한 지점의 주변 상,하,좌,우를 살펴본 뒤에 주변 지점중에서 값이 '0' 이면서 아직 방문하지 않은 지점이 있다면 해당 지점을 방문한다
2. 방문한 지점에서 다시 상,하,좌,우를 살펴보면서 방문을 진행하는 과정을 반복하면, 연결된 모든 지점을 방문할 수 있다
3. 모든 노드에 대하여 1~2번 과정을 반복하며, 방문하지 않은 지점의 수를 카운트한다
