크루스칼 알고리즘이란?

• 그래프의 각 정점을 최소 비용으로 연결하기 위해 사용하는 알고리즘
• 이는 신장 트리에서 간선의 가중치가 최소가 되는 트리를 구하는 과정과 동일함

신장 트리(Spanning Tree)

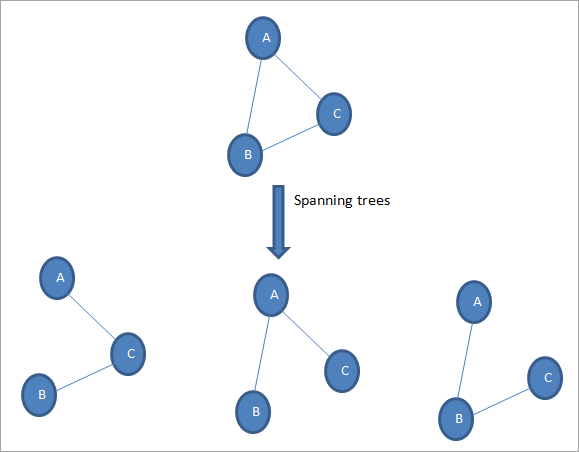
• 신장 트리란 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미
  이는 트리의 성립 조건과도 일치함
• 최소 신장 트리는 여러 신장 트리 중에서 간선의 가중치합이 최소가 되는 트리를 의미함

알고리즘 동작 과정

1. 간선을 가중치 순서대로 정렬
2. 가중치가 작은 간선부터 시작해 각 정점을 연결해줌, 이 때 신장 트리를 만족하는 조건을 확인하기 위해서는 Union-Find알고리즘 사용
   Union-Find 알고리즘: 각 정점마다 연결된 조상 노드를 체크해 두 정점의 부모 노드가 같으면 동일한 트리에 이미 연결된 것으로 판단하는 알고리즘

예시

프로그래머스 - 섬 연결하기

문제

n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.

다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.

제한 사항

• 섬의 개수 n은 1 이상 100 이하입니다.
• costs의 길이는 ((n-1) * n) / 2이하입니다.
• 임의의 i에 대해, costs[i][0] 와 costs[i][1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i][2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
• 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
• 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
• 연결할 수 없는 섬은 주어지지 않습니다.

입출력 예

섬의 개수가 7개이고, 배열이 [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] 인 경우 출력은 4가 되어야 함

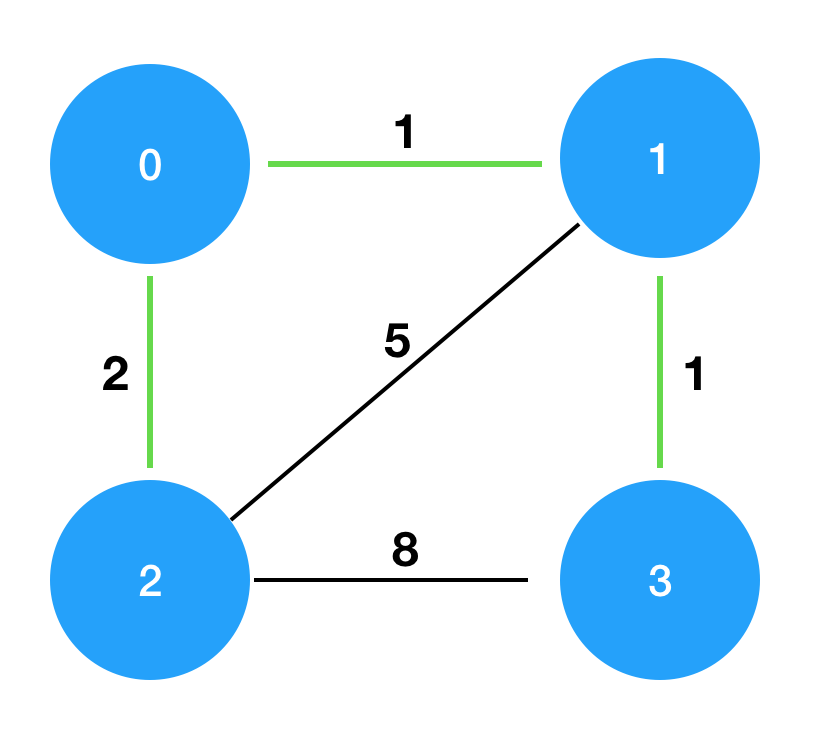
풀이

function solution(n, costs) {
  	// 각 간선을 가중치 순서대로 정렬해줌
    const roadMap = costs.sort((a, b) => a[2] - b[2]);
  
  	// 자신의 부모 노드를 표시해주는 배열을 생성, 이 때 초기값은 자기자신으로 설정
    const connected = [];
    for (let i = 0; i < n; i++) connected.push(i);
  
    let answer = 0;
  	// 가중치가 작은값부터 순회를 진행
    for (let i = 0; i < roadMap.length; i++) {
        const [start, end, length] = roadMap[i];
        const parentStart = getParent(connected, start);
        const parentEnd = getParent(connected, end);
      
      	// 간선에 붙은 정점의 조상 노드를 확인해 같으면(=이미 연결되어있으면) 생략
        if (parentStart === parentEnd) continue;
      	// 두 신장 트리를 하나의 신장 트리로 합치는 과정
      	// 이 때 방향의 일관성을 위해 조상노드의 값을 비교해 조상노드값이 작은쪽이 부모가 되도록 트리를 붙여줌
        if (parentStart < parentEnd) connected[parentEnd] = start;
        else connected[parentStart] = end;
      
      	// 가중치값 더해주기
        answer += length;
    }
    return answer;
}

// 조상 노드를 확인하는 함수
// 부모 노드를 거슬러 올라가 parent를 반환함
function getParent(array, n) {
    if (array[n] === n) return n;
    else return getParent(array, array[n]);
}