Multi-Head Attention(MHA)

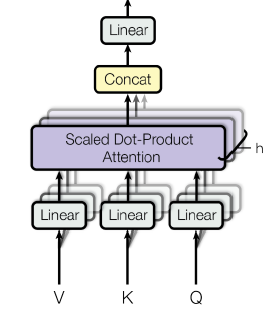
기본 구조는 이전 포스팅에서 다룬 transformer와 동일하게 Q, K, V를 입력으로 받고 Scaled-Dot Product Attention을 수행해서 Encoding vector를 얻는다.

다른 점은 transformer가 겹쳐있는 구조라는 것이다. 즉, 하나의 입력 세트인 Q, K, V를 공유하지만 병렬적으로 서로 다른 Attention 연산을 수행한다. 후에는 산출된 여러 개의 Encoding vector를 concatenate해서 하나의 encoding vector를 얻고 이에 대해서 linear transform을 수행한다.

이를 수식화하면 아래와 같다.

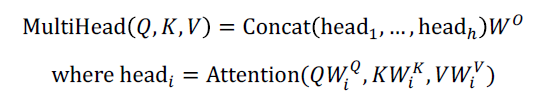
Q, K, V는 동일하지만 W는 i번째 head에 대해서 개별적으로 존재한다. 동일한 입력에 대해서 전혀 다른 attention 연산을 수행하도록 하기 위함이다. 이 때 사용되는 서로 다른 Attention들을 head라고 부르고, 이러한 head들이 여러개 있기 때문에 Multi-head attention이다.

Multi-head인 이유

하나의 attention에서 하나의 feature를 바라본다는 관점인 것 같다. 가령, 특정 문장의 행동을 중점적으로 바라보는 attention이 있을 수 있다. 혹은 문장에서 나타나는 장소들에 대해서 중점적으로 바라보는 attention들이 있을 수 있다. 이러한 attention들을 모아서 한번에 여러 개의 의미들을 뽑을 수 있는 모듈을 기대하기 위함이다.

도식화

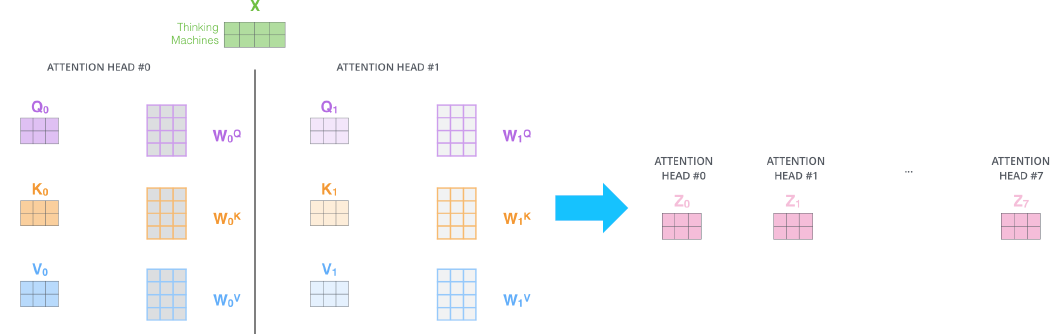
하나의 attention의 수행 과정은 이전 포스팅에서 다룬 것과 동일하다. 단지 이러한 attention을 병렬적으로 수행해서 여러 개의 encoding vector를 얻는 것이 다른 점이다.

뽑아낸 encoding vector들을 concatenate해보자.

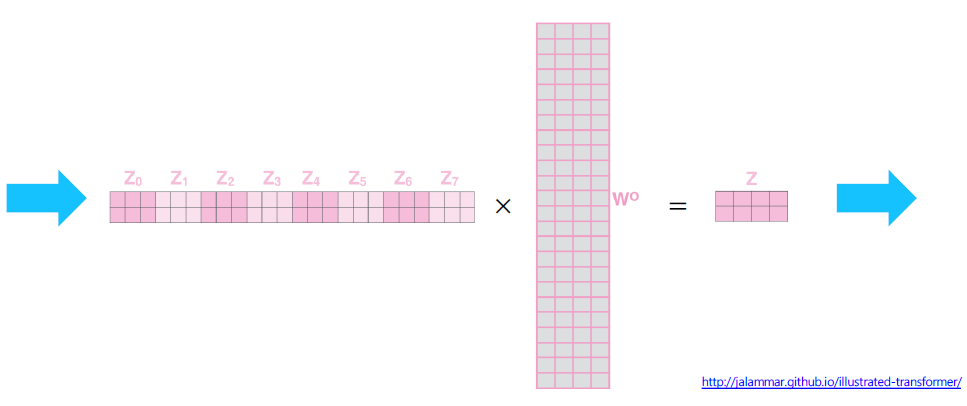
concatenate된 vector에 linear transform을 수행한다. 여기서 기대하는 것은 차원 수를 줄이는 것이다.

Complexity

• $n$: sequence length
• $d$: dimensino of representation
• $k$: kernel size of convolutions
• $r$: size of the neighborhood in restricted self-attention

Complexity per Layer

Self-Attention

Self-Attention의 하나의 layer에서 계산되어야 하는 수식은 아래와 같다.

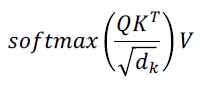
여기서 주된 연산은 $QK^T$이다. $QK^T$는 shape은 $(n\times d)\times (d\times n)$이고 이는 $d$번의 곱셈 연산을 $n^2$번 수행하는 것과 동일하다. 즉, 여기서의 time complexity를 Big O로 표현하며 $O(n^2\cdot d)$이다.

하지만 행렬 연산의 병렬화에 특화된 장치로써 GPU를 사용하는 것이 일반적이다. 따라서 GPU 자원이 무한정 많다는 가정하에, Sequence의 길이가 아무리 길어져도 $QK^T$는 $O(1)$의 complexity를 가진다고 생각할 수 있다.

Recurrent

RNN에서의 complexity는 $O(n \cdot d^2)$이다.

RNN hidden state의 dimension을 d라고 하자. 매 step마다 hidden state에 linear transform 연산을 수행해서 다시 hidden state vector를 출력해야하기 때문에, $W_h$의 dimension은 (d, d)라고 할 수 있다.

즉, 매 step마다 d번의 곱셈을 d번 수행하는 한번의 행렬 내적 연산을 수행한다. 이러한 과정을 sequence의 길이만큼 n번 수행해야 하기 때문에 $O(n \cdot d^2)$의 complexity를 계산할 수 있다.

이 또한 GPU 자원이 무한히 큰 가정을 가정해서 complexity를 다시 생각해볼 수 있지만, 그럼에도 time complexity는 $O(n)$으로 밖에 줄이지 못한다. 왜냐하면 근본적으로 n번의 step을 수행해야 되는 RNN의 특성 상, 병렬화를 통해 n번의 step을 구현할 수 없기 때문이다.

Memory

위 표에서 메모리에 관한 내용을 분석할 수 있다.

$d$는 hyperparamter이다. 사용자의 컴퓨팅 환경에 따라서 가변적으로 변할 수 있다.
하지만 $n$은 sequence의 길이이기 때문에, 사용자가 관여할 수 없는 값이다.

모델이 메모리를 사용한다는 것의 의미는 backward-propagation과 forward-propagation을 수행한 결과들이 메모리에 저장된다는 것이다. 이 때, 메모리에 저장되는 값들의 크기에 관여하는 것은 $n$이다.

Transformer의 경우 Q, K, V를 통해 한꺼번에 행렬들이 계산되어야한다. 마치 time complexity가 $O(n^2\cdot d)$로 계산된 것과 같이 $n^2$에 비례하는 형태로 메모리 요구된다.

반면 RNN은 $n$에 비례하게 메모리가 요구된다.

Path length

최악의 경우를 가정하기 위해서 sequence의 끝단에 위치한 token이 sequence의 처음에 위치한 token에 접근하기 위해서 필요한 path lenght를 계산해보자.

• Transformer: $O(1)$이다.
  key와 value로 접근이 한번에 이루어지기 때문이다. 왜냐하면 근접해있는 token이든 굉장히 멀리 있는 token이든 attention의 가중치를 크고 낮게 해줌에 따라 한번에 해당 token의 정보르 사용하기 때문이다.
• RNN: $O(n)$이다. n번의 step을 거쳐야 하기 때문이다.

요약

• Transformer: 더 빠른 학습, 더 많은 메모리, 빠른 path 접근
• RNN: 느린 학습, 더 적은 메모리, 느린 path 접근

Transformer: Block-Based Model

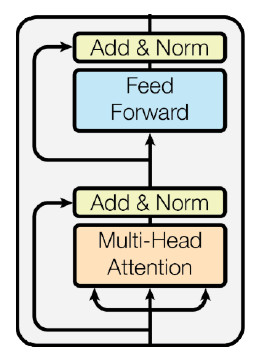
Multi-head attention을 재료로하여 하나의 transformer block을 만들 수 있다.

Residual connection

network의 layer가 깊어질 때, gradient vanishing을 해결하고 학습을 안정화시켜준다. ResNet이 이전의 network들과는 다르게 layer가 깊어질 수록 학습이 잘 되는 효과를 기대할 ㅅ 있다.

$LayerNorm(x+sublayer(x))$

Residual connection에서는 단순히 입력과 네트워크 출력을 더해줘서 새로운 출력을 만든다. 즉, 입력과 출력에 대한 차이를 네트워크가 출력하도록 하는 것이다. 이를 수식화하며 아래와 같다.

$H(x) = F(x) + x$
$F(x) = H(x) - x$

block-based model의 출력을 H(x)라 하고, Multi-head attention의 출력을 F(x)라고 하자. Residual block에서는 위와 같이 H(x)가 정의되기 때문에 Multi-head attention의 원하고자하는 출력에 대한 차이값을 학습하게 된다.

Residual connection의 dimension

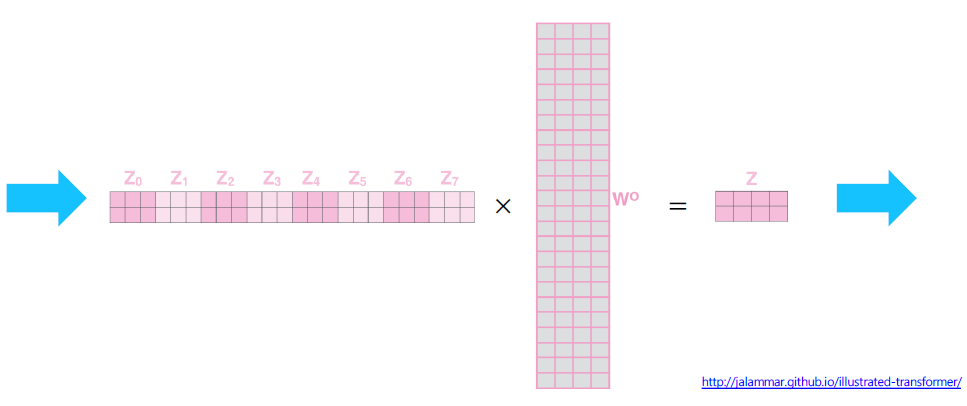
Multi-head attention에서 concatenate된 정보를 줄이는 이유가 여기있다. 왜냐하면 Residual connection을 통해서 $F(x)$와 $x$를 더하기 위해서는 vector의 차원이 동일해야하기 때문이다.

Layer normalization

variables의 평균을 0, 분산을 1로 만들고 우리가 원하는 평균과 분산을 주입하기 위한 선형변환 과정이다.

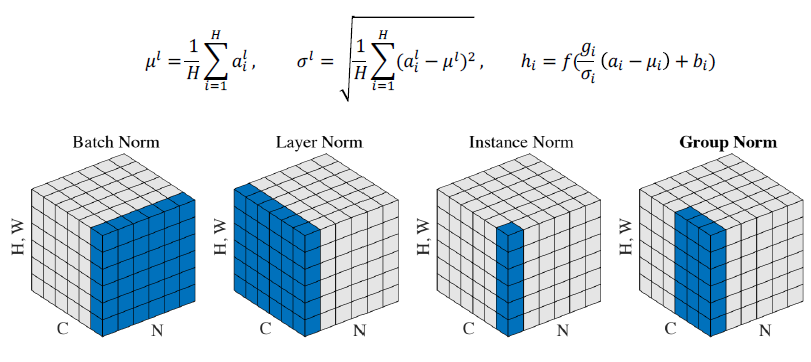
normalization 진행 과정
1. input vector로 [3, 5, -2]가 들어왔다고 하자.
2. normalization은 이 값들을 평균이 0, 분산이 1이 되도록 변형한다.
3. $y=ax+b$에 input vector를 넣는다.
4. input vector는 $y$로 선형변환되는데, $x$에 비해서 분산은 $a$배, 평균은 $+b$가 된다.
5. model은 gradient descent와 같은 학습 과정을 통해 layer마다 적절한 $a와 b$를 학습한다.

---

Layer normalization 수행 과정

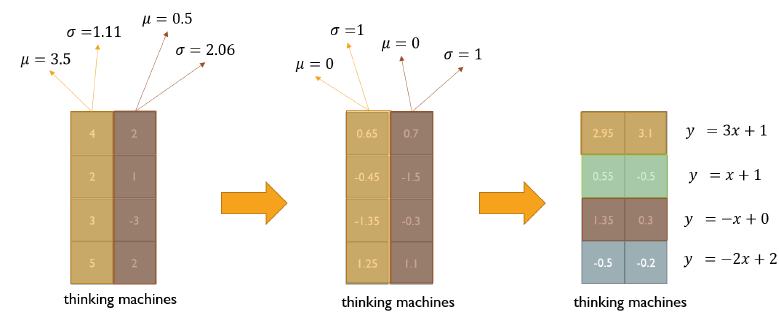
1. word 별로 평균을 0, 분산을 1로 만들어준다. (vector의 column 기준)
2. vector의 row별로 affine transformation을 수행한다.

ref: affine transformation wiki

Feed Forward

Fully connected layer다. 이외의 residual connection, layer normalization은 이전과 동일하다.

정리

입력의 word vector와 동일한 형식으로 output vector가 출력된다.

Positional encoding

transformer에서의 순서성

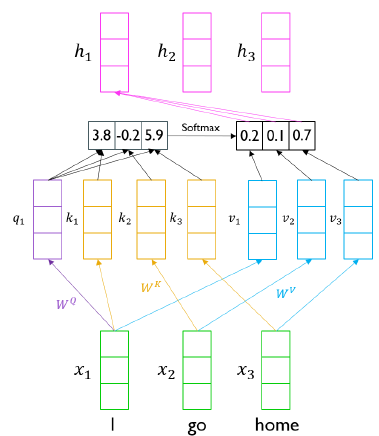
Q, V, C 계산을 위한 도식을 다시 보자. 입력 vector인 [I, go, home]은 순서가 달라져도 결과에 영향을 끼치지 않는다. 즉, [home, go, I]로 바뀐다하더라도 'I'에 해당하는 encoding vector의 내용은 순서가 바뀔지언정 내용물이 바뀌지 않을 것이다.

즉, RNN과 같이 순서에 민감하게 반응하는 network와 다르게 transformer는 입력 vector를 집합과 같이 인식한다. Sequence의 순서성을 transformer에서 고려하기 위해 고안된 것이 positional encoding이다.

e.g., 첫번째 인덱스에는 1000을 더해주자!

sin, cos

transformer에서는 sin, cos 함수를 통해 positinoal encoding을 구현했다.

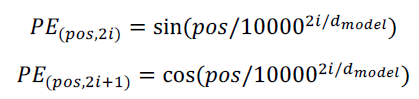
짝수번째 dimension에서는 sin을, 홀수번째 dimension에서는 cos을 사용했다.

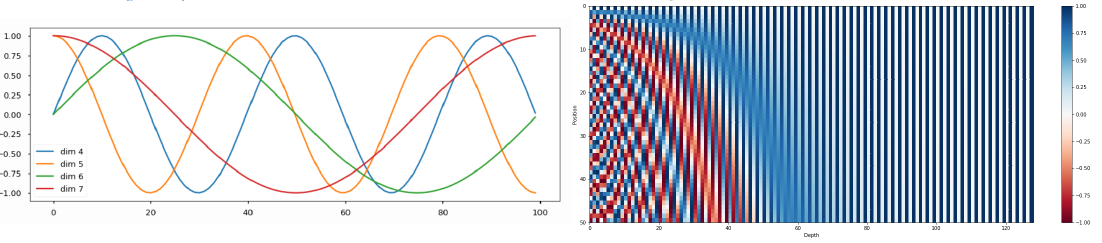
단순한 정수의 배열(e.g., 1, 2, 3, ...)이 아니라 sin, cos을 사용하는지에 대해 내가 이해하고 부스트캠프 팀원들끼리 이해한 바는 다음과 같다.
1. unique한 값을 어느 정도 보장.
2. 주기성을 갖기 때문에 쉽게 표현 가능.

이에 대한 답은 아래 링크에 있는 것 같은데 아직 제대로 이해하지 못했다.
ref: https://skyjwoo.tistory.com/entry/positional-encoding%EC%9D%B4%EB%9E%80-%EB%AC%B4%EC%97%87%EC%9D%B8%EA%B0%80

Warm-up learning rate scheduler

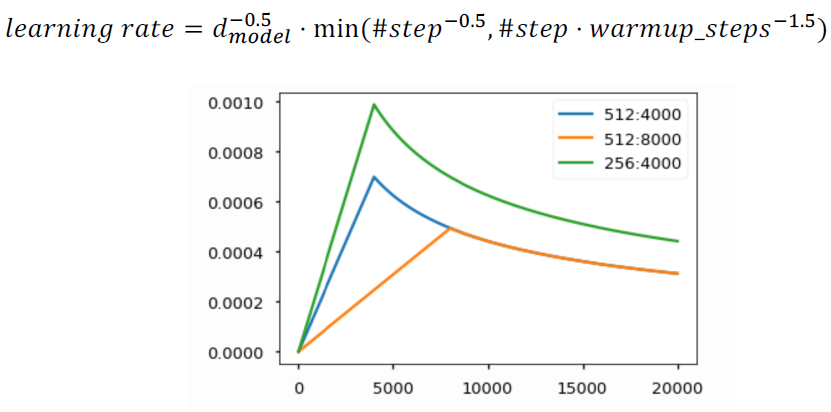
요점은 gradient가 클 때는 보다 큰 learning rate를, gradient가 작을 때는 보다 작은 learning rate를 적용하고자 하는 것이다.

transformer에서는 이를 실현하기 위해 위 수식과 같이 step별로 다른 leraning rate를 적용하도록 적용했다고 한다. 즉, gradient의 값에 따라 learning rate가 달라지는 것이 아니라 step에 의존되도록 learning rate scheduler를 구현했다.

Encoder 정리

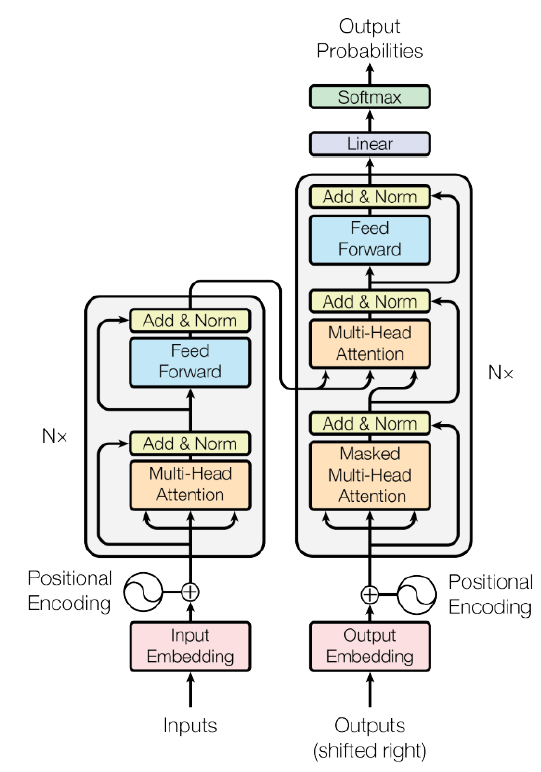
1. Input으로 word vector를 준다.
2. Positional Encoding을 통해 순서성을 부여한다.
3. 도식에서 'Nx'이라고 보이는데, 이는 Block-based model을 N번 쌓는다는 의미다. 보통 6, 12, 24개로 쌓는다.
4. Input vector와 같은 차원의 Encoding vector를 얻는다.

시각화

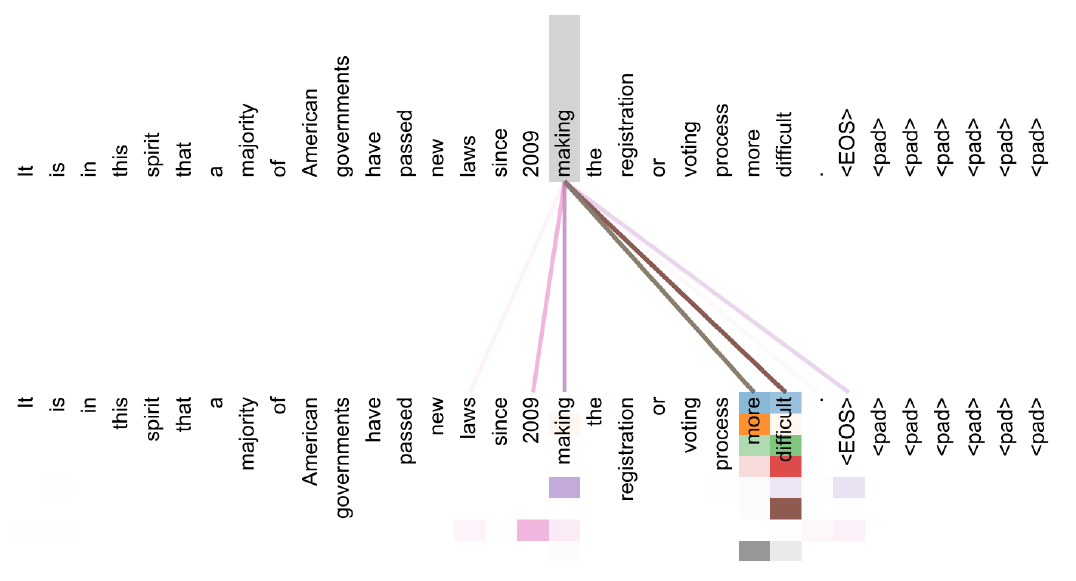
아래의 문장이 input이고 위 문장이 attention에서 input을 어떻게 바라보는지 나타낸 것이다.
아래 문장을 보면 하나의 단어에 대해서 여러 grid가 발생하는데, MHA의 여러 출력을 나타낸 것이다.

making이라는 단어는 2009라는 시간 정보와 more, difficult를 매우 중점적으로 보고 있음을 알 수 있다.

Decoder

• Outputs: 'I go home'이 input이었다면 '나는 집에 간다'가 outputs일 것이다. 이를 Shifted right해서 '[SoS] 나는 집에 간다'를 Embedding vector로서 decoder에 넣는다.
• Positional encoding: encoding의 그것과 동일하다.
• Masked MHA, Add & Norm: Seq2Seq with attention에서 decoder의 hidden state를 뽑는 과정과 동일하다고 생각하면 된다.
• MHA: encoding vector는 Value와 key로, decoder hidden state는 query로 들어간다. Seq2Seq with attention에서 encoder hidden state에 가중치를 걸어서 decoder hidden state와 결합하는 부분에 해당한다.
• Linear: decoder vector를 language vocabulary만큼 변환해준다. 한글 vocabulary vector의 dimension이 10만개라면, decoder vector를 10만 차원으로 변환한다.
• Softmax: language vocabulary에 대응되도록 vector가 만들어졌기 때문에 softmax를 통과시키는 것만으로도 다음 단어를 예측할 수 있다.

Masked self-attention

순서를 고려하지 않는 transformer의 특성 때문에 sequence의 모든 정보들이 Q와 K를 곱할 때 계산된다. 하지만 seuqence 상에서 앞단에 위치한 정보들이 뒷단에 위치한 정보들을 보지 말아야 하는 경우도 존재한다.

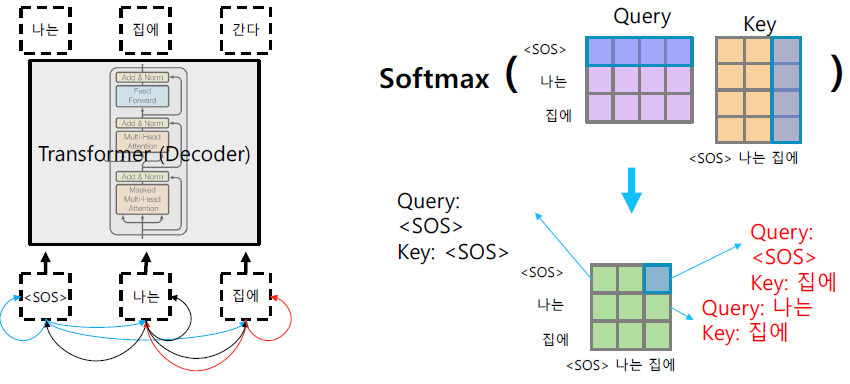
가령, 모델을 구성할 때 [SOS]는 [SOS]만을 참조해야 하고, '나는'은 뒤에 오는 '집에'를 참조하지 말아야 한다고 해보자. 그리고 보통의 경우 이렇게 뒷단의 정보를 보지 말아야 하는 경우가 발생한다!

이러한 정보들간의 참조 결과는 위 도식과 같이 $Softmax(QK^T)$에 표현된다. sequence의 후단 정보들을 무시하기 위해서 아래와 같은 기법을 사용한다.

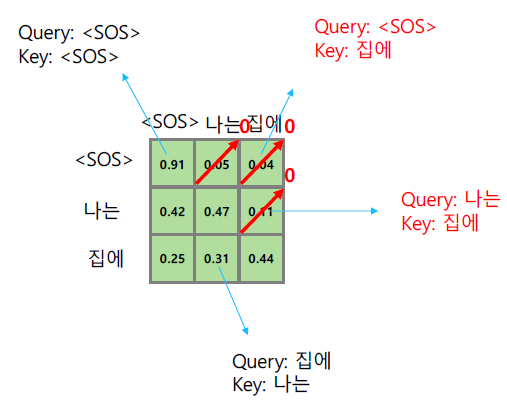
1. 대각성분 위의 정보들을 0으로 만든다.
2. 나머지 softmax 결과값들은 row를 기준으로 합이 1이 되도록 조정한다.

Performance

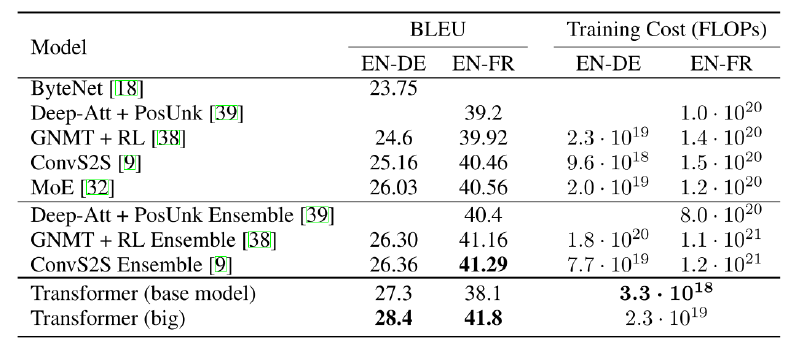
기존의 방법론들과 transformer 모두 BLEU score가 20, 40 정도이다. BLUE는 최대치가 100이기 때문에 매우 좋지 않은 성능이라고 생각할 수 있다. 하지만, bi, tri gram 등을 통해 측정한 수치이기 때문에 저 정도 수치만 되도 상용 번역기의 성능이라고 한다.
BLEU 포스팅에서 다뤘듯이 '나는 수학을 공부한다.'와 '나는 수학을 열심히 공부한다.'는 다른 문장이기 때문에 발생하는 이슈다.