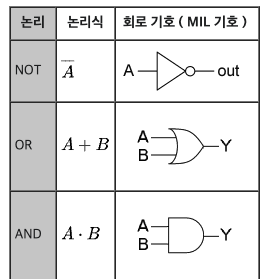
지금까지 정리한 논리 게이트를 모아보면 아래와 같이 NOT, AND, OR, NAND, NOR게이트가 있다.
 |
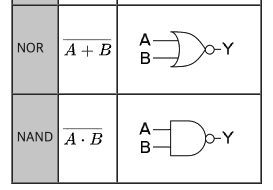 |
위 그림에 보면 논리식이라고 해서 식이 나와 있다. 즉, 논리게이트(논리연산)를 논리식으로 표현이 가능하다. 여기서 나온 논리식은 부울 대수식을 사용한다. CPU나 메모리를 만들려면 논리게이트(전자회로)의 조합으로 만들 수 있는데 이 과정을 수식화하면 이해가 빠르게 될 것 같다.
기본 연산
-
NOT 연산
NOT게이트의 진리표와 같이 NOT연산은 아래와 같다.(프라임부호(')가 붙으면 NOT연산이다.)0' = 1 | 1' = 0 -
AND 연산
AND게이트의 진리표와 같이 AND연산은 아래와 같고, 마치 곱하기처럼 표현할 수 있다.0•0 = 0 | 0•1 = 0 | 1•0 = 0 | 1•1 = 1아래 그림은 Y = A•B 또는 Y = AB 라고 표현할 수 있다.
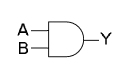
-
OR 연산
OR 게이트의 진리표와 같이 OR연산은 아래와 같고, 마치 더하기처럼 표현할 수 있다.0 + 0 = 0 | 0 + 1 = 1 | 1 + 0 = 1 | 1 + 1 = 1아래 그림에서는 Y = A + B 라고 표현할 수 있다.
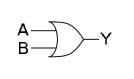
그러면 아래 그림은 어떻게 표현할까?(이게 바로 XOR게이트이다.)
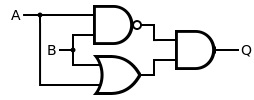
NAND게이트는 (AB)' , OR게이트는 A + B , NAND게이트와 OR게이트를 AND게이트로 묶으니까 Q = (AB)'(A+B)라고 표현할 수 있다.
기본 법칙
gpt선생님의 도움을 아래와 같이 받았다.
부울 대수식에는 여러 가지 중요한 기본 정리가 있습니다. 이러한 정리들은 부울 대수식을 단순화하고 논리 회로를 최적화하는 데 도움을 줍니다. 아래는 부울 대수식의 주요 기본 정리 중 일부입니다:
등가성 정리 (Identity Theorem):
- A + 0 = A
- A * 1 = A
이 정리는 OR 게이트에서 0을 더하거나 AND 게이트에서 1을 곱할 때 결과가 변하지 않음을 의미합니다.
- 지배적 정리 (Domination Theorem):
- A + A'B = A
- A * A' = 0
이 정리는 어떤 신호 A와 그의 상반신호 A'가 함께 있을 때, A는 A'B에 의해 지배된다는 것을 의미합니다.
- 공항법칙 (Idempotent Law):
- A + A = A
- A * A = A
이 정리는 같은 신호를 OR 게이트나 AND 게이트에 여러 번 연결하더라도 결과가 변하지 않음을 의미합니다.
- 보수 법칙 (Complement Law):
- A + A' = 1
- A * A' = 0
이 정리는 어떤 신호 A와 그의 보수 A'를 OR 게이트나 AND 게이트에 연결하면 항상 1 또는 0이 됨을 의미합니다.
- 교환법칙 (Commutative Law):
- A + B = B + A
- A B = B A
이 정리는 OR 또는 AND 연산에서 입력의 순서를 바꿔도 결과가 같음을 의미합니다.
- 분배법칙 (Distributive Law):
- A (B + C) = (A B) + (A * C)
- A + (B C) = (A + B) (A + C)
이 정리는 곱셈과 덧셈 간의 분배 법칙을 나타냅니다.
- 드모르간의 정리 (De Morgan's Theorem):
- (A + B)' = A' * B'
- (A * B)' = A' + B'
이 정리는 논리 회로의 NAND 또는 NOR 게이트를 AND와 OR 게이트로 변환하는 데 사용됩니다.
이러한 기본 정리들을 적절하게 조합하고 활용하여 부울 대수식을 단순화하고 논리 회로를 최적화할 수 있습니다. 부울 대수식을 잘 이해하고 이러한 정리를 활용하는 것은 디지털 논리 회로 설계와 관련된 작업에서 중요합니다.
위 정리들을 보면 대부분 일반적인 수식과 같이 받아들여지는데 2가지 정도가 직관적으로 이해가 안 된다. 하나는 분배법칙 중 A + (B C) = (A + B) (A + C) 이고, 다른 하나는 드보르간의 정리이다. 그래서 이 2가지를 증명해보도록 하겠다.
-
A + (B C) = (A + B) (A + C) 증명
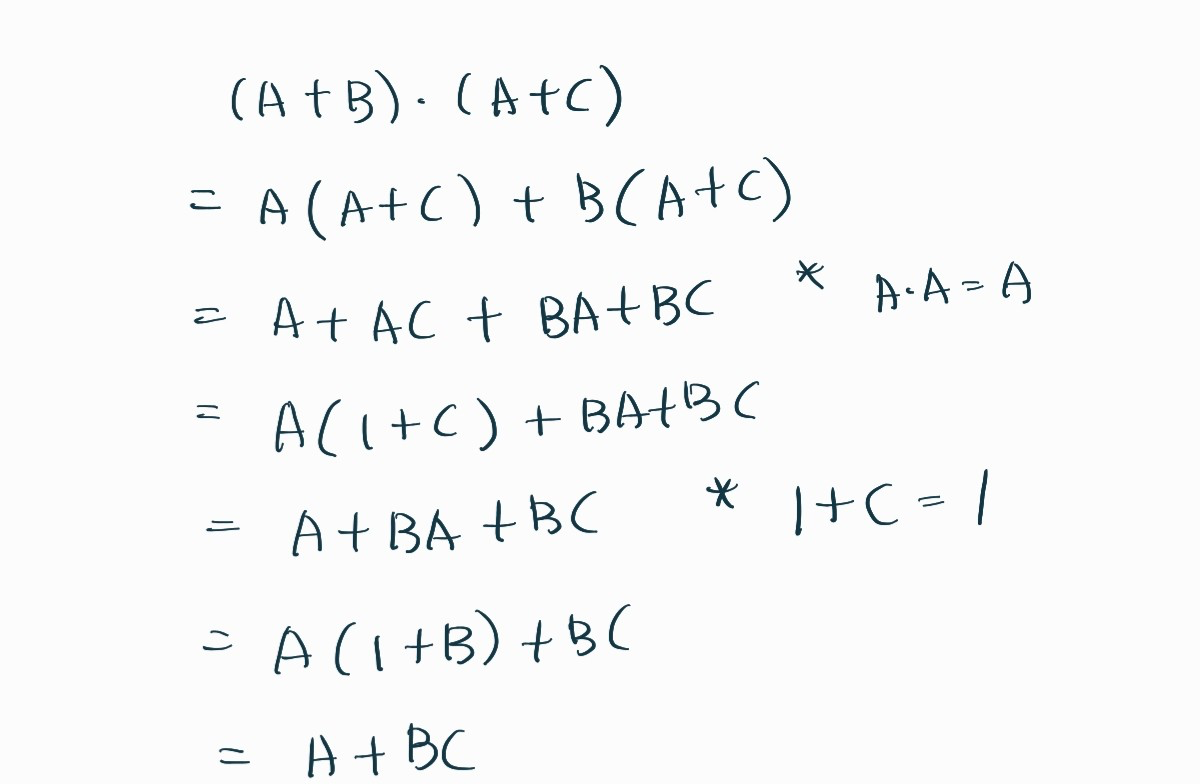
-
(A * B)' = A' + B' 증명
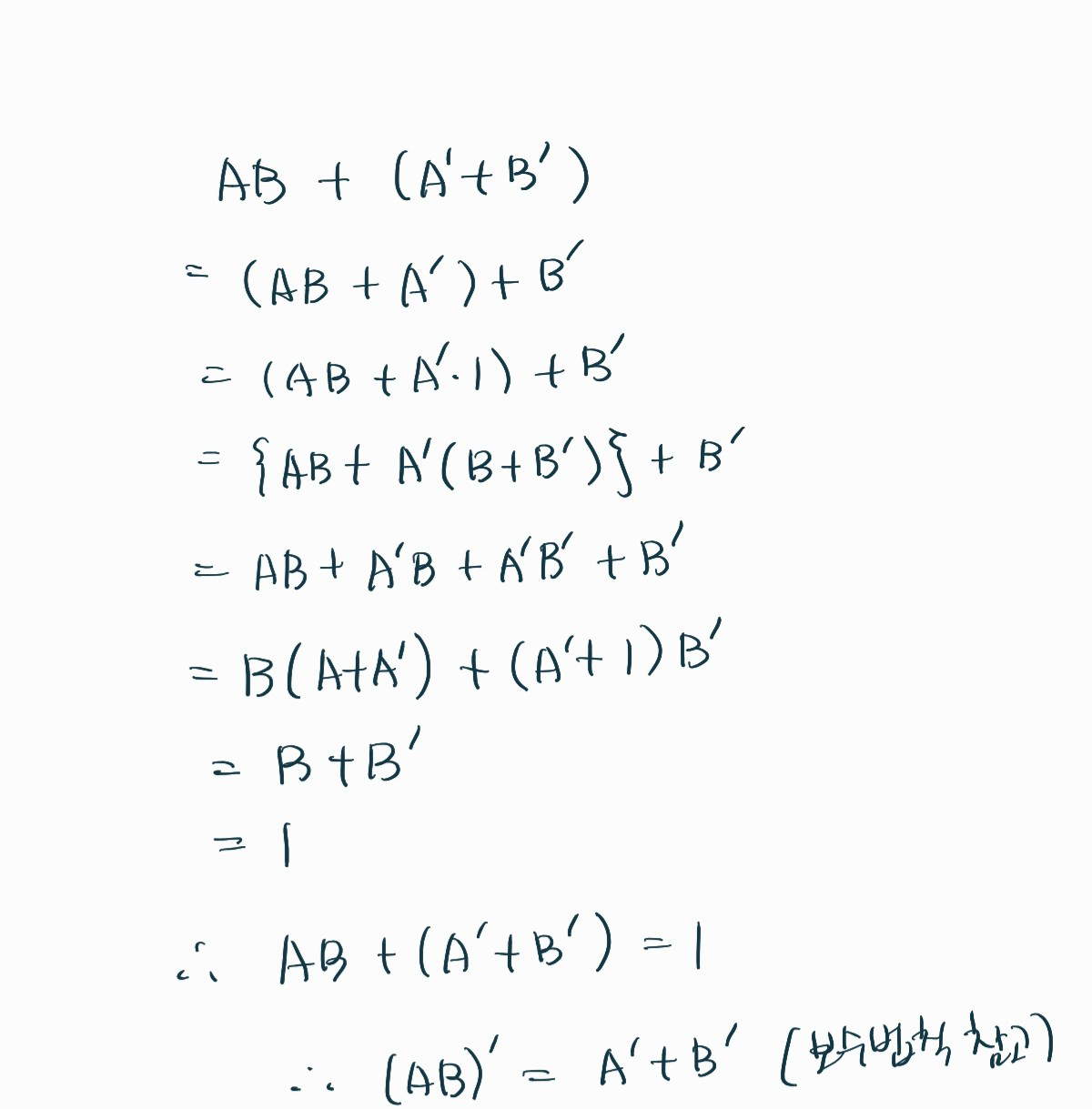
이쯤하니 증명은 괜히 했다 싶으다...
참고사이트 :
https://ko.wikipedia.org/wiki/XOR_%EA%B2%8C%EC%9D%B4%ED%8A%B8
https://ko.wikipedia.org/wiki/%EB%85%BC%EB%A6%AC_%ED%9A%8C%EB%A1%9C
