지금까지 정리한 논리게이트들을 모아서 가산기(덧셈 연산을 수행하는 논리회로)를 만들어보자. 가산기를 만들기 전에 비트의 개념을 알고 가자. 처음엔 1bit 가산기를 만들 것이기 때문이다.
bit
bit는 binary digit의 약자이다. 즉, 하나의 비트는 2진수의 한자리로 0이나 1의 값을 가질 수 있다.
XOR게이트
A와 B가 0과 1만의 값을 가질 때(즉, A와 B가 각각 1bit일때), 자리 올림을 무시하고 A와 B를 더하는 경우의 수를 생각해보자.
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
위 표처럼 A와 B를 더하면 C로 표현이 될 것이다. A와 B 모두 1인 경우가 C가 0이 되는 것은 일단 자리올림을 무시했기 때문이다.(나중에 자리올림도 처리한다.)
지금까지 정리한 NOT, AND, OR, NAND, NOR게이트 중에 위의 표처럼 값을 출력할 수 있는 회로는 없었다. 그래서 똑똑한 사람들이 논리게이트를 섞어서 위의 표와 같이 출력이 가능한 아래 그림과 같은 XOR게이트를 만들었다.
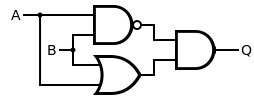
전에 부울 대수식으로 표현하면 위 회로는 Q = (AB)'(A+B)라고 표현 가능하다. 이 식을 잘 정리하면 Q = A'B + AB'이다. 즉, A와 B가 다른 값을 가져야만 Q가 1이 되어 위에 A와 B를 더하는 경우와 같이 표현 가능하다. XOR게이트도 자주 쓰이기 때문에 아래와 같은 심벌을 가지고 있다.
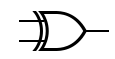
반가산기
XOR게이트는 A와 B 각 1bit를 더할 때 자리올림수는 표현하지 못 했다. 이번에는 자리올림수까지 표현이 가능한 회로를 만들어보자. 자리올림을 carry라고 하여 자리올림수를 C라고 하고, 1의 자리수를 S(sum)라고 하자. 그러면 A와 B가 각 1bit일 때 더하는 경우는 다음 표와 같다.
| A B | C S |
|---|---|
| 0 0 | 0 0 |
| 1 0 | 0 1 |
| 0 1 | 0 1 |
| 1 1 | 1 0 |
위의 표와 같이 나타낼 수 있는 회로는 XOR게이트와 AND게이트를 섞어서 아래 그림과 같이 만들 수 있다.(진짜 똑똑한 사람들 많은 것 같다.)
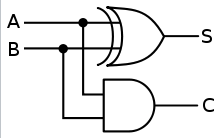
이렇게 두 bit를 덧셈할 수 있는 회로를 반가산기(half adder)라고 한다.
참고사이트 :
https://ko.wikipedia.org/wiki/%EA%B0%80%EC%82%B0%EA%B8%B0
https://ko.wikipedia.org/wiki/XOR_%EA%B2%8C%EC%9D%B4%ED%8A%B8
https://ko.wikipedia.org/wiki/%EB%B9%84%ED%8A%B8_(%EB%8B%A8%EC%9C%84)
