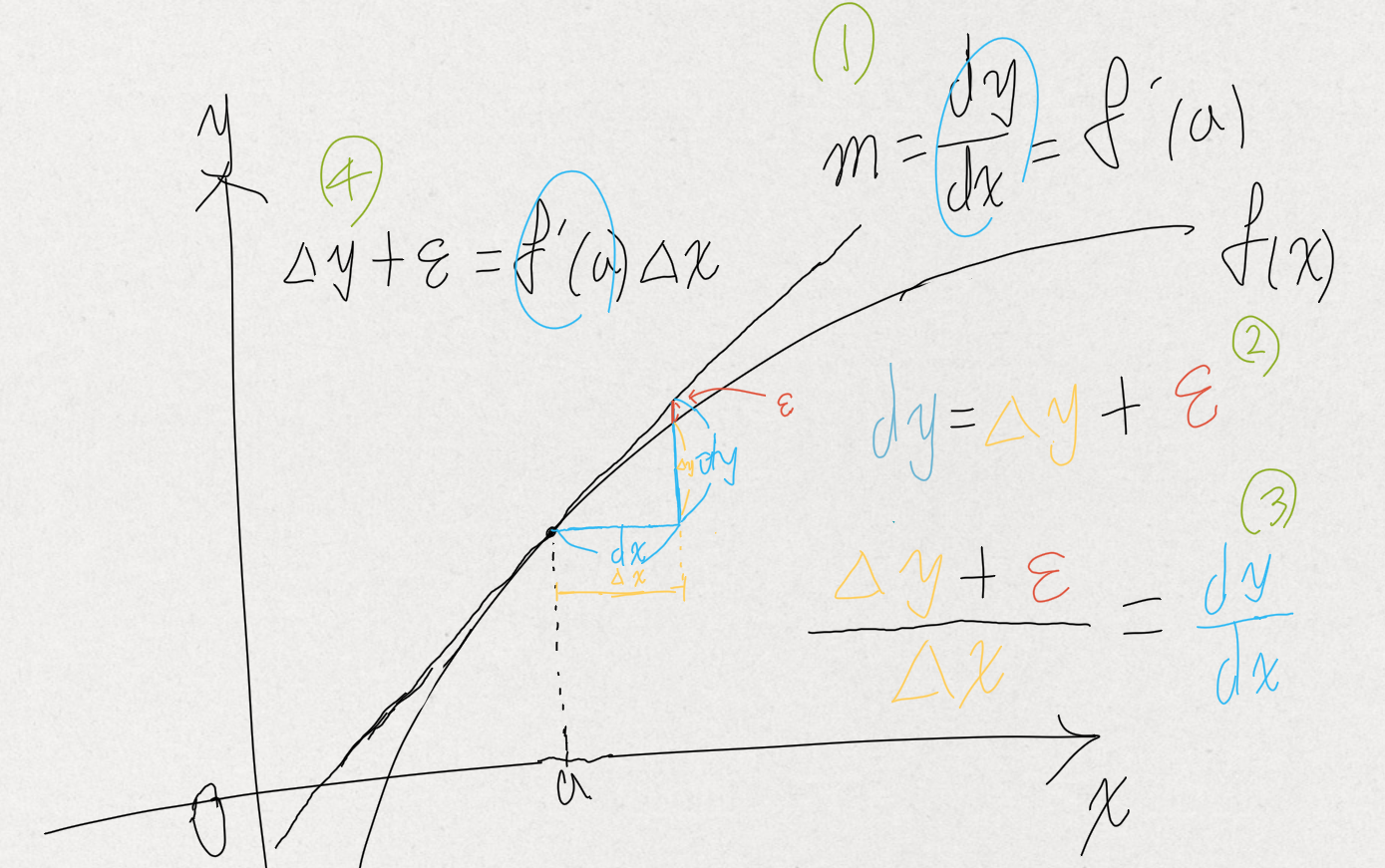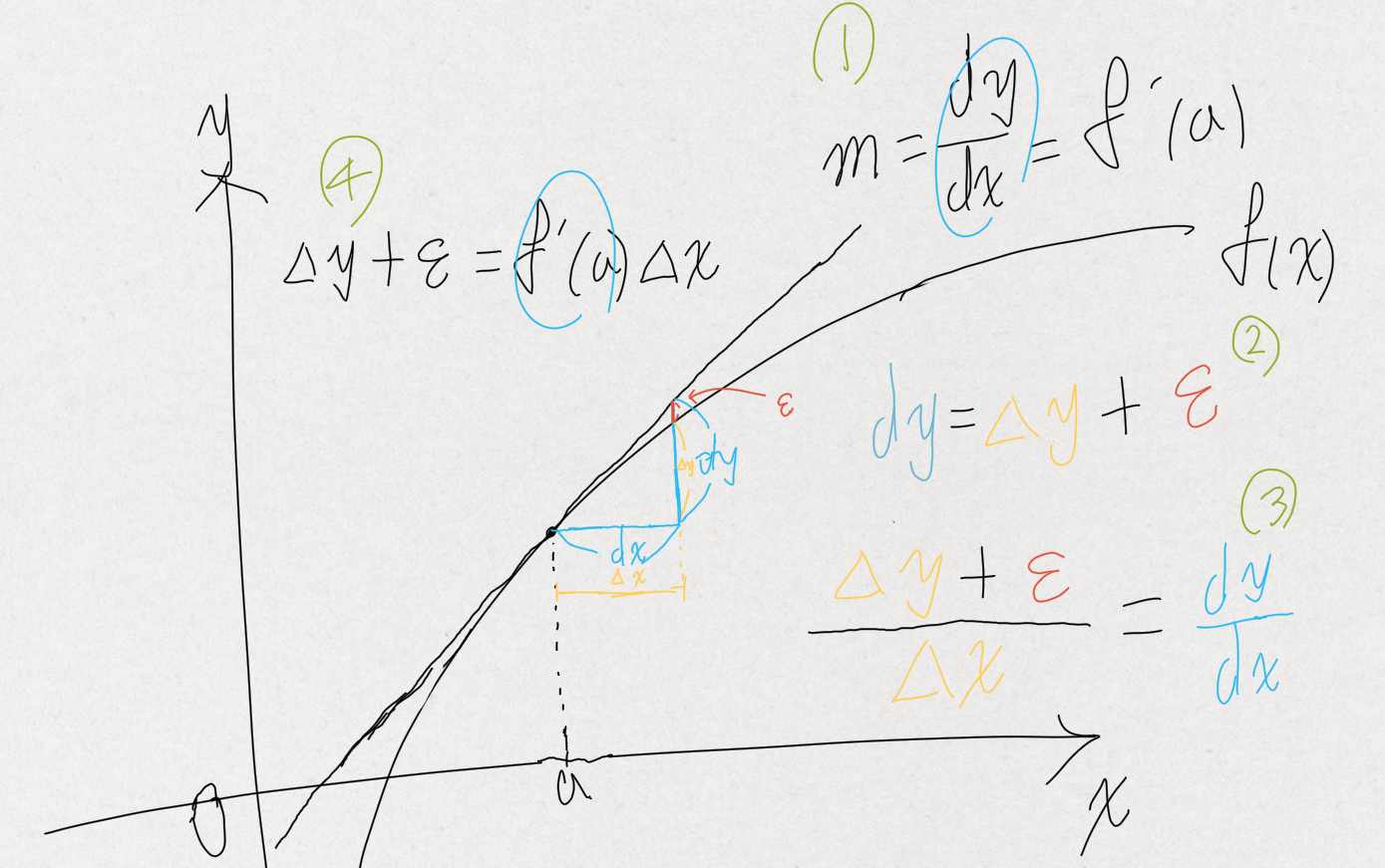필자가 보는 책(Man Sik Min · Hyeong Chul Jeong · Hyejung Lee, 『CALCULUS』, 한티미디어)에는 Chain Rule 의 증명이 소개되어 있지 않기에, Stewart 선생님의 Calculus 를 보고 그 내용을 정리하려 한다.

0. 주의

 필자는 수포자이며, 수학을 전공하지도 않았다. 필자가 공부한 내용을 잊지 않고 환기하기 위해 정리한 글이므로 잘못된, 혹은 더 나아가 틀린 설명이 존재할 수 있다.

 따라서 이하의 내용은 어느정도 걸러듣고, 틀린 내용에 대해선 가감없이 댓글 작성 부탁드립니다.

1. The Chain Rule

If $f(u)$ is differentiable at the point $u = g(x)$ and $g(x)$ is differentiable at $x$, then the composite function $(f \circ g)(x) = f(g(x))$ is differentiable at $x$, and...

$(f \cdot g)(x) = f'(g(x)) \bullet g'(x)$

In Leibniz's notation, if $y = f(u)$ and $u = g(x)$, then

$\cfrac{dy}{dx} = \cfrac{dy}{du} \cdot \cfrac{du}{dx}$

where $dy/du$ is evaluated $u = g(x)$.

 필자가 읽고 있는 책에서는 다음과 같이 Chain Rule 을 소개하고 있다. 위 내용은 어느 정도 납득 가능한 수준의 내용이다. 왜냐하면 Leibniz 의 표기를 통해 $du$ 의 변화에 따른 $dy$, 그리고 $dx$ 의 변화에 따른 $du$ 는 곧 합성 함수의 변화율을 의미하기 때문이다.

 $u$ 가 $x$ 에 대해 두 배 빠르게 증가하고 $y$ 가 $u$ 에 대해 세 배 빠르게 증가한다면 $x$ 에 대한 $y$ 의 변화는 6 배 빠르게 이뤄진다고 생각해볼 수 있다.

2. Proof of the chain rule (Incomplete)

$\Delta{u}$ 를 $\Delta{x}$ 에 대한 $u$ 의 변화량이라고 한다면 아래와 같이 작성할 수 있다:

위와 마찬가지로 $y$ 의 변화량은 다음과 같이 쓸 수 있다:

이를 # 1. The Chain Rule 에 나온 Leibniz 표기법을 통해 작성하게 되면 이하와 같다:

$\lim\limits_{\Delta{x} \to 0}{\cfrac{\Delta{y}}{\Delta{u}}}$ 와 $\lim\limits_{\Delta{x} \to 0}{\cfrac{\Delta{u}}{\Delta{x}}}$ 는 모두 수렴하므로 위와 같이 limits law 에 따라 분리가 가능하다.

- The reasons that converge

1. $\lim\limits_{\Delta{x} \to 0}{\cfrac{\Delta{u}}{\Delta{x}}}$ 는 이미 선행 조건으로 $g(x)$ 가 differentiable 하다고 했으므로 당연히 수렴. Pass

2. $\lim\limits_{\Delta{x} \to 0}{\cfrac{\Delta{y}}{\Delta{u}}}$ 에 대해서는 한번 생각을 해봐야 하는데...

   • $y = f(u)$ 는 미분 가능(선행 조건)하다. 따라서 다음의 식은 수렴한다(극한값이 존재한다): $\lim\limits_{\Delta{u} \to 0}{\cfrac{\Delta{y}}{\Delta{u}}}$
   • $g(x)$ 가 미분 가능하므로 연속이고, 연속이 되기 위해선 $\lim\limits_{\Delta{x} \to 0}\{{g(x + \Delta{x}) - g(x)}\} = 0$ 가 성립해야 한다. ($x$ 인 순간의 극한값과 함수값이 동일해야 하므로 빼면 $0$ 이 나와야 한다)
   • 그러므로 $\Delta{x} \to 0$ 는 곧 $\Delta{u} \to 0$ 를 의미한다.
   • 따라서 $\lim\limits_{\Delta{x} \to 0}{\cfrac{\Delta{y}}{\Delta{u}}} = \lim\limits_{\Delta{u} \to 0}{\cfrac{\Delta{y}}{\Delta{u}}}$ 이므로 수렴.

---

 이어서 $\Delta{x} \to 0$ 가 $\Delta{u} \to 0$ 인것을 확인 했으므로 다시 아래와 같이 정리할 수 있다:

 얼핏보면 완벽한 증명으로 보이지만 실제론 반쪽짜리 증명이다. 왜냐하면 ($\Delta{x} \neq 0$ 인 순간에도) $\Delta{u} = 0$ 인 경우에는 써먹을 수 없기(0 으로 나누는 행위는 수학적으로 정의되지 않기) 때문이다.

 그러나 Chain Rule 은 $\Delta{u}$ 가 $0$ 인 순간에도 사용 가능한 공식이다. 그러므로 실제 증명에서는 위와 같은 (분모가 0 이 되는 상황을 만드는) 방식으로 접근하지 않는다.

3. How to prove the Chain Rule

- Background

$y = f(x)$ 에 대해서 $x$ 의 값이 $a$ 에서 $a + \Delta{x}$ 으로 변할 때, $y$ 의 증분을 아래와 같이 표현한다:

미분의 정의에 따라 $f'(a)$ 는 아래와 같이 쓸 수 있다:

여기에 $\varepsilon$ 이라는 것이 있고 이는 $\cfrac{\Delta{y}}{\Delta{x}}$ 와 $f'(a)$ 의 차로 정의된다고 했을 때

 미분에 정의에 따라 위와 같이 쓸 수 있고, 또한 $\varepsilon$ 을 $\Delta{x} = 0$ 일때 $0$ 이라 정의하게 되면, $\varepsilon$ 은 $\Delta{x}$ 에 대해 연속인 함수가 된다. (극한값과 함수값이 같으므로)

 $\varepsilon$ 에 대한 식을 $\Delta{y}$ 에 대한 식으로 정리하면 아래와 같이 쓸 수 있게 된다:

 왜 $\Delta{y} = f'(a)\Delta{x} - \varepsilon\Delta{x}$ 인지 쉽게 이해가 되지 않을 수 있다. 여기에서 말하는 $\Delta{x}$ 그리고 $\Delta{y}$ 는 $f'(x)$ 의 $dy/dx$ 와는 약간 다르므로 아래의 삽화를 준비했다:

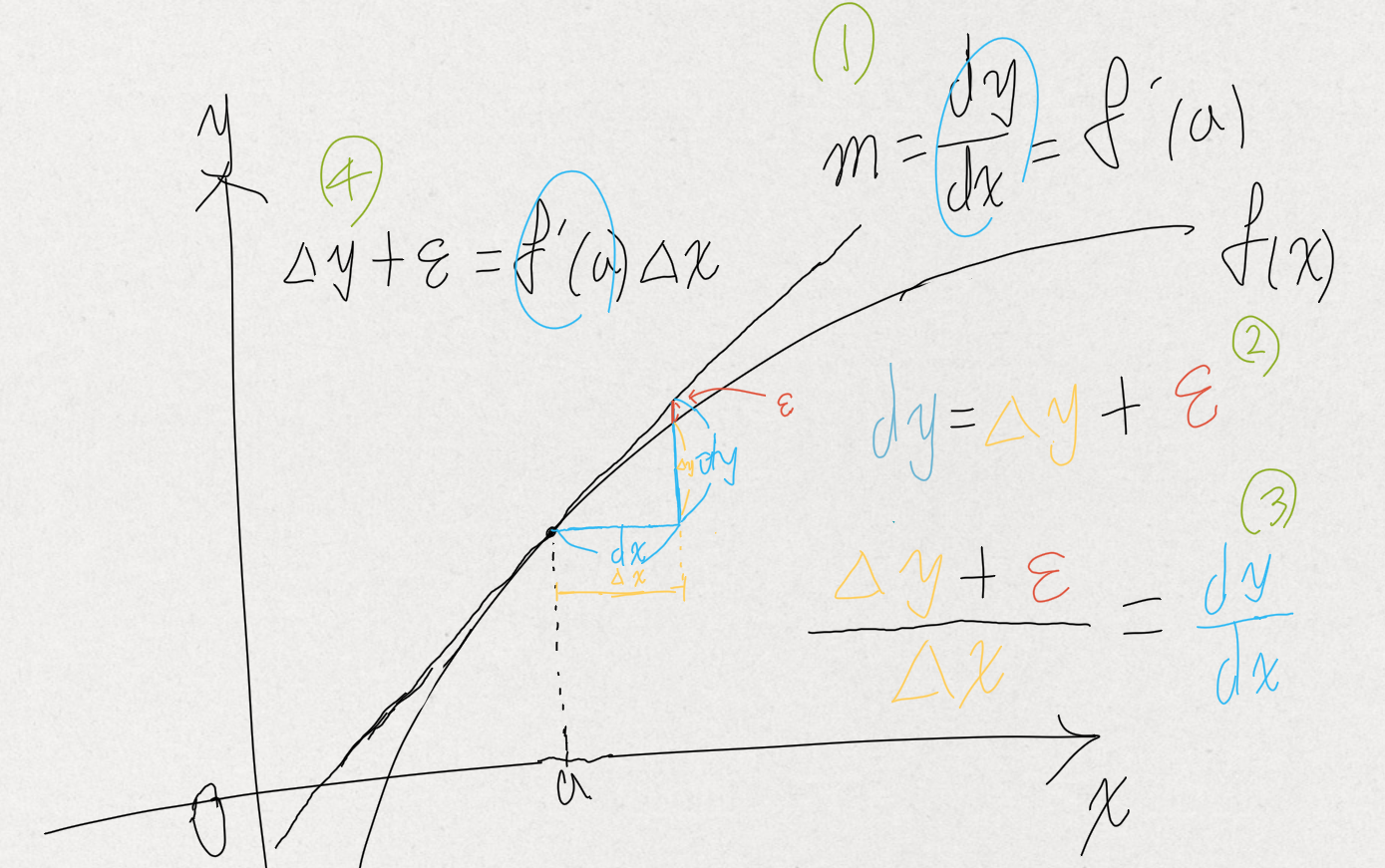
 위에서 보는 것처럼 $dx/dy$ 자체는 $f'(a)$ 순간에서의 기울기를 나타내고 있으나 실제 함수 $f(x)$ 와 비교하면 아주 근소한 차이가 존재한다. 이를 의미하는 $\varepsilon$ 으로 이해해야 한다.

 또한 $\varepsilon$ 은 $\Delta{x}$ 가 $0$ 인 순간에는 $0$ 으로 정의된다는 것을 주목하라. 이를 통해 $\varepsilon$ 이 $\Delta{x}$ 에 대해 연속인 함수가 될 수 있기 때문이다.

 위에서 정의한 $\varepsilon$ 을 기반으로 하여 Chain Rule 을 증명해보려 한다.

- Proof of the Chain Rule

 $u = g(x)$ 가 $a$ 에서 미분 가능하고, $y = f(u)$ 가 $b = g(a)$ 에서 미분 가능하다. $\Delta{x}$ 를 $x$ 의 증분, 그리고 $\Delta{u}$ 와 $\Delta{y}$ 가 각각 $u$ 와 $y$ 의 증분이라 한다면, 우리는 위에서 정의한 $\varepsilon$ 을 이용해 아래와 같이 정의가 가능하다:

위와 마찬가지로 $\Delta{y}$ 역시 아래와 같이 정의되어질 수 있다:

$\Delta{y}$ 방정식의 등장하는 $\Delta{u}$ 를 치환하여 아래의 식을 얻을 수 있다:

구하고자 하는 $dx/dy$ 는 아래와 같다:

 The reasons that converge 에서 설명했듯이 $\Delta{x} \to 0$ 는 $\Delta{u} \to 0$ 와 동일하므로 $\varepsilon_1$ 과 $\varepsilon_2$ 모두 $0$ 으로 가게 된다. 따라서 위 극한을 전개하여 풀어쓰면 아래와 같다:

이로써 Chain Rule 이 성립함을 증명하였다.

출처

[책] Man Sik Min · Hyeong Chul Jeong · Hyejung Lee, 『CALCULUS』, 한티미디어, p104.
[사이트] https://vegatrash.tistory.com/17
[동영상] https://www.youtube.com/watch?v=yAG2acoURtk