프로그래머스 Lv.2 | 타겟 넘버

깊이/너비 우선 탐색(DFS/BFS)

출처 : 위키백과

1. 깊이 우선 탐색 (DFS)

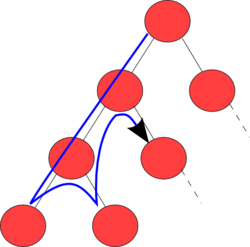
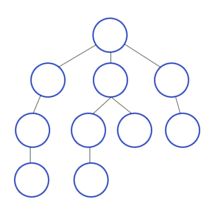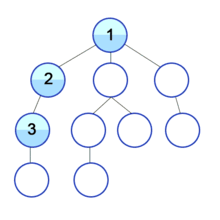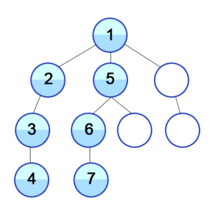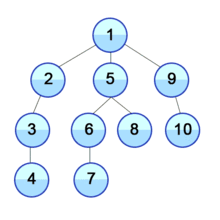
def DFS( 그래프(리스트), 시작점, 방문여부 확인할 리스트=[ ] ):
	방문 여부 확인할 리스트.append(시작점)
	
	for 노드 in그래프[시작점]:
		if 노드가 방문하지 않은 거라면 (node not in 리스트):
			DFS(그래프(리스트), 노드, 방문여부 확인 리스트)
	return 방문여부 리스트

DFS(graph, 'A')

2. 너비 우선 탐색 (BFS)

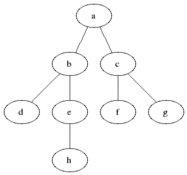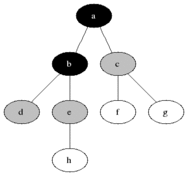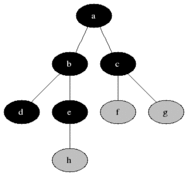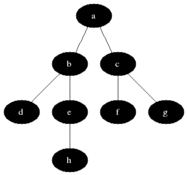
보통 큐를 사용해서 BFS를 사용한다.

graph = {
'A' :  ['B']
'B' :  ['C', 'D', 'E']
....
}

def BFS(graph, start_node):
    visited = [ ]
    queue = [ ]

    queue.append(start_node)
    
    while queue:
        node = queue.pop(0) #FIFO 구조를 지키기 위해?
        if node not in visit: # 방문 경로에 없으면 노드를 추가해준다.
            visit.append(node)
            queue.extend(graph[node]) 
    return visited  

[ 추가 설명 ]
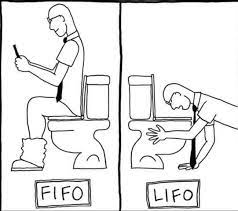
Queue : FIFO 구조 (First in, First Out)
Stack : LIFO 구조 (Last in , First Out)

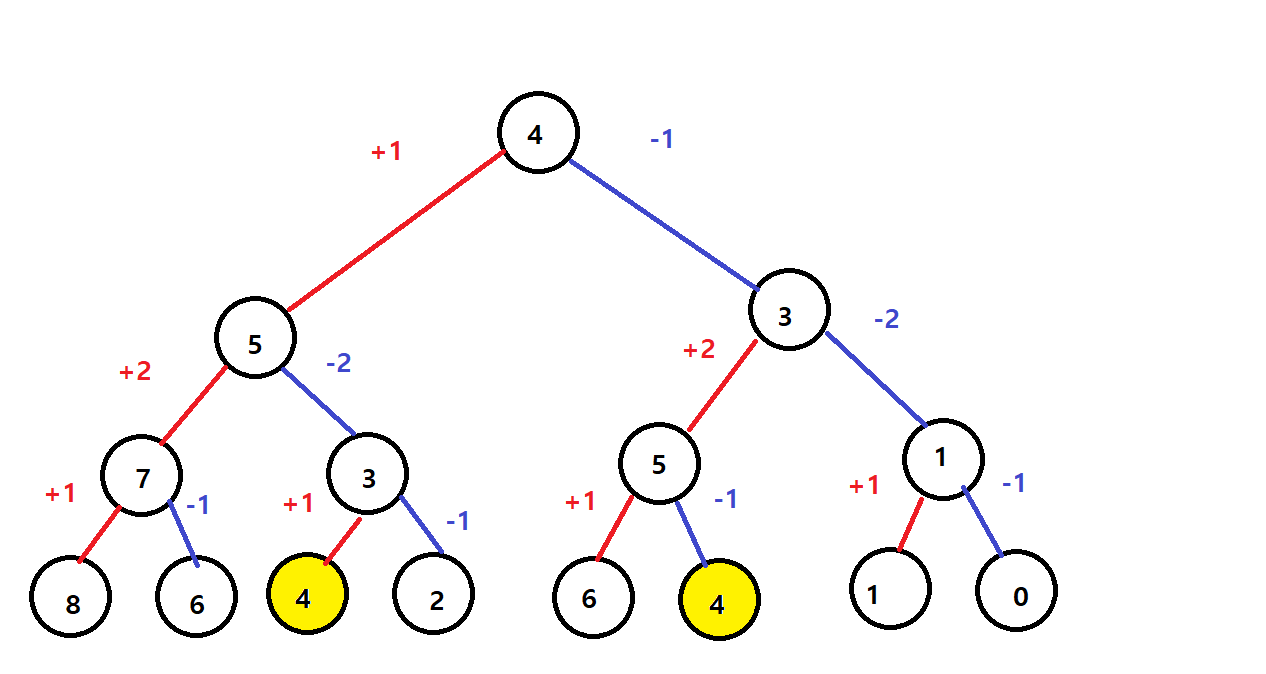
문제

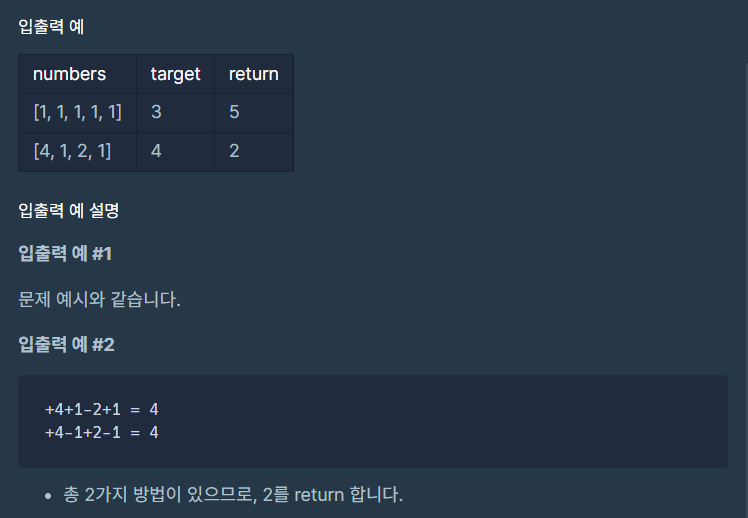
어떻게 해야할까

계산되는 경우의 수를 세주는 방법이다.
다행히 곱하거나 나누는 방식은 없다. 더하거나 빼기만 하면 된다.

문제의 유형이 DFS/BFS 다. DFS/BFS는 진짜 기억이 잘 안난다. 잠시 구글링을 하고 와야지..
DFS => 깊이 우선 탐색 (스택 또는 재귀함수), BFS => 너비 우선 탐색(큐)
왼쪽은 더하기 오른쪽은 빼기 해서 맨 밑에 나오는 값이 원하는 값으로 나오는 부분을 더하면 되려나?
(옛날에 알고리즘이나 자료구조에 비슷한 과제를 했었던 것같다.)

일단 그냥 일반적으로 for문을 돈다하면 시간 복잡도가 무시무시하게 커질 것이 분명하다. DFS일 것 같은 느낌이 든다. 스택 또는 재귀 함수로 구현을 하라고? 아마 재귀가 제일 편리할 것같은데 문제는 내가 재귀에 진짜 취약하다는 점😱

이러다가 하루종일 걸릴 것같아서 질문 글을 살짝 보았는데 뭔가 힌트를 잡은 것같아서 한번 다시 생각 시작.
아예 처음부터 다 더하고 거기서 원하는 목표의 숫자를 빼기. 그러면 얼마만큼의 숫자가 필요한지 알게된다. 그걸 다시 분해해서 계산하기..?

재귀함수로 어떻게 해야하지?

이건 그냥 배워가는 느낌으로 문제를 풀어야겠다. 다음 유형땐 잘 풀면 되지 뭐 ㅎㅎ,,
일단 내가 바로 앞에서 생각한 순서도를 만들어봤다.

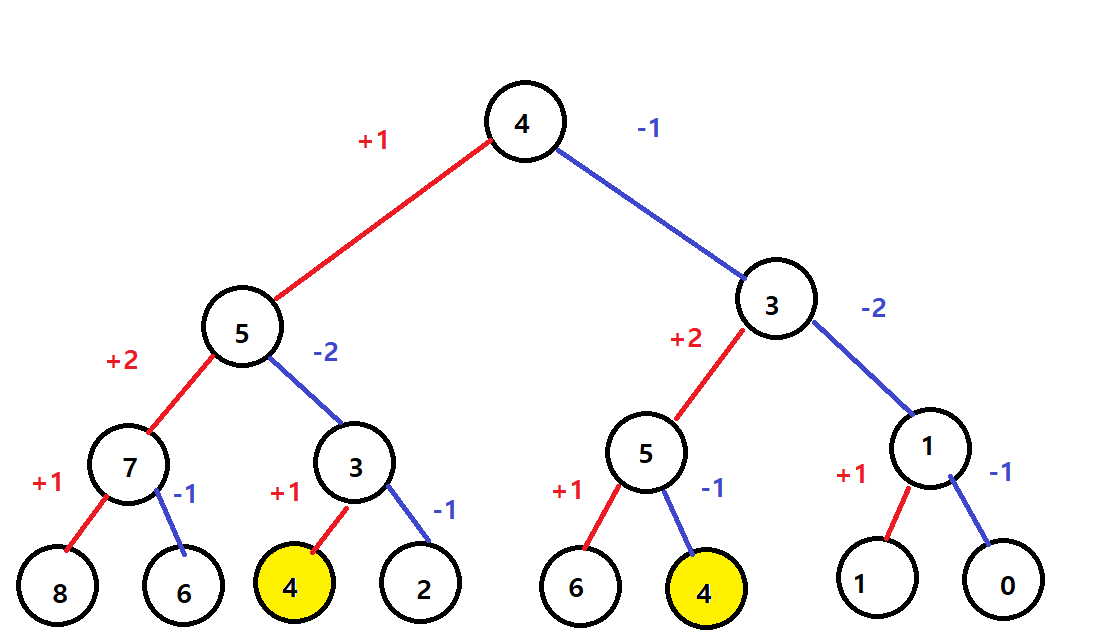
이걸 어떻게 재귀함수랑 엮냐 이거지.. 내가 아는 재귀함수는 팩토리얼이나 피보나치밖에 없는데요 ㅠㅠ

def recursive(array, n):
	n+=1
	if n == len(array):
		return 
	return array[n]*1 (or -1)

대충 이런식이려나?

코드

DFS는 높이로 탐색하니까 재귀함수의 break point는 높이가 MAX인 상태일 때.
재귀할 땐 어떤 기준으로 나눠줘야할까. 일단 더하기 빼기이니까 -1를 곱하거나 아닐 때.
구글링했을 때 내 접근 방식과 매우 비슷한 재귀함수를 선택했다.

최종코드

맞추긴 했는데 이건 그냥 참고하면서 한거랑 마찬가지라서 그냥... 배워간다 생각하자.
어떻게 바로 생각이 나시는걸까.. ㅠㅠㅠ