CH 9 Priority Queues, Heaps, and Graphs

Huisu·2021년 12월 11일

C python 자료구조

DataStructure

목록 보기

9/10

Priority Queues

Priority Queue

Queue의 item들 사이에 우선 순위가 존재하는 것
- ex1) item 값이 클수록 우선 순위가 높다
- ex2) item 값이 작을수록 우선 순위가 높다
높은 우선 순위를 가진 요소가 언제라도 접근 가능한 위치에 존재하는 Queue
Dequeue를 실행했을 때 우선 순위가 높은 순서대로 Dequeue

Implementation Level

Unsorted List
- 우선 순위가 높은 item 찾기 O(N)
- 우선 순위가 높은 item Dequeue O(1)
- item이 삭제된 자리가 비어 있기 때문에 뒤에 존재하는 item들 한 칸씩 앞으로 Shift O(N)
Array-Based Sorted List
- 우선 순위로 정렬돼 있기 때문에 item 삭제는 O(1) 삭제된 부분을 메꾸기 위해 Shift O(N)
- Enqueue 진행하면 우선 순위에 따른 item 위치 찾기 O(N), Insert O(1), 넣을 자리 마련하기 위해 item들 뒤로 한 칸씩 Shift O(N)
Linked Sorted List
- Enqueue 시에 new item의 우선 순위에 따른 위치를 찾기 위해 O(N)
Binary Tree
- 평균적으로 item의 위치를 찾는 데 O(log N)
- 정렬 리스트를 tree로 구현한 것처럼 tree가 선형이라면 item 위치 탐색에 O(N)
- Enqueue와 Dequeue 모두 평균적으로 O(log N)
Heap
- Priority Queue를 저장하기에 제일 자연스러운 방식
- 찾기, Enqueue, Dequeue 모두 O(log N)

PQType.h

class FullPQ {};
class EmptyPQ {};
#include "Max_Heap.h"

template<class ItemType>
class PQType
{
public:
	PQType(int max);        
	~PQType();            
	void MakeEmpty();
	bool IsEmpty() const;
	bool IsFull() const;
	void Enqueue(ItemType newItem);
	void Dequeue(ItemType& item);
private:
	int length;
	HeapType<ItemType> items;
	int maxItems;
};

PQType Method

Enqueue
- length ++
- element 마지막에 newitem 넣기
- ReHeapUp으로 우선 순위로 정렬

template<class ItemType>
void PQType<ItemType>::Enqueue(ItemType newItem)
{
	if (length == maxItems)
		throw FullPQ();
	else
	{
		length++;
		items.elements[length - 1] = newItem;
		items.ReheapUp(0, length - 1);
	}
}

Dequeue
- item에 제일 우선 순위가 높은 elements[0] 저장
- elements[0] 자리에 우선 순위가 낮은 length-1 번째 item 덮어씌우기
- length-1 번째 아이템 삭제 (length --)
- ReHeapDown

template<class ItemType>
void PQType<ItemType>::Dequeue(ItemType& item)
{
	if (length == 0)
		throw EmptyPQ();
	else
	{
		item = items.elements[0];
		items.elements[0] = items.elements[length - 1];
		length--;
		items.ReheapDown(0, length - 1);
	}
}

PQType.cpp

template<class ItemType>
PQType<ItemType>::PQType(int max)
{
	maxItems = max;
	items.elements = new ItemType[max];
	length = 0;
}

template<class ItemType>
void PQType<ItemType>::MakeEmpty()
{
	length = 0;
}

template<class ItemType>
PQType<ItemType>::~PQType()
{
	delete[] items.elements;
}

template<class ItemType>
void PQType<ItemType>::Dequeue(ItemType& item)
{
	if (length == 0)
		throw EmptyPQ();
	else
	{
		item = items.elements[0];
		items.elements[0] = items.elements[length - 1];
		length--;
		items.ReheapDown(0, length - 1);
	}
}

template<class ItemType>
void PQType<ItemType>::Enqueue(ItemType newItem)
{
	if (length == maxItems)
		throw FullPQ();
	else
	{
		length++;
		items.elements[length - 1] = newItem;
		items.ReheapUp(0, length - 1);
	}
}

template<class ItemType>
bool PQType<ItemType>::IsFull() const
{
	return length == maxItems;
}

template<class ItemType>
bool PQType<ItemType>::IsEmpty() const
{
	return length == 0;
}

Time Complexcity

Implementation	Enqueue	Dequeue
Heap	O(logN)	O(logN)
Linked-List	O(N)	O(N)
BST (Balanced)	O(logN)	O(logN)
BST (Skewed)	O(N)	O(N)

Heaps

Heap

조건 1 모양, 조건 2 순서
모양: Complete Binary Tree
- 어떤 node가 child node를 하나만 가지는 경우 left child에만 존재해야 함
Max heap
- 모든 node에 대해 그 값이 children보다 크거나 같아야 함
- 최대값이 root에 존재
Min heap
- 모든 node에 대해 그 값이 children보다 작거나 같아야 함
- 최소값이 root에 존재
Array Representation
- Heap은 Complete tree이기 때문에 array 구현이 간편
- Binary Search Tree와 다르게 Array 중간이 비는 경우가 없음
- 다음 depth로 내려가기 위해서는 해당 depth의 모든 칸이 채워져야 하는 Complete tree이기 때문
- Linked list보다 Array 구현이 간편
- 실제 Heap은 Array로 구현되어 있고 Complete tree 모양은 관념적으로 기억

ReHeapDown

node를 delete했을 때 중간 부분이 비어 complete tree가 되지 않음
위에서 heap이 깨졌을 때 밑으로 가면서 heap으로 다시 만들어 주는 함수
자신과 자신의 Child랑 비교했을 때 Child 중에 자기 자신보다 큰 애가 있는 경우
해당 node와 child node 중 큰 node랑 swap
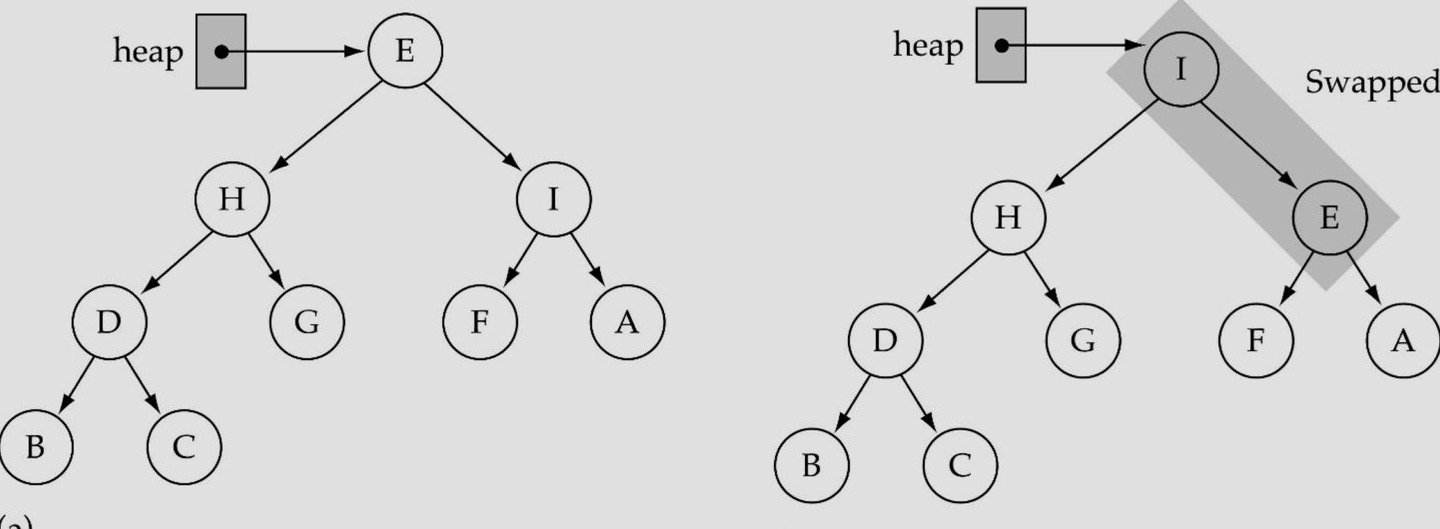
Recursive

template<class ItemType>
void HeapType<ItemType>::ReheapDown_re(int root, int bottom)
{
	int maxChild;
	int leftChild = root * 2 + 1;
	int rightChild = root * 2 + 2;

	if (leftChild <= bottom)
	{
		if (leftChild == bottom)
			maxChild = leftChild;
		else
		{
			if (elements[leftChild] <= elements[rightChild])
				maxChild = rightChild;
			else
				maxChild = leftChild;
		}
		if (elements[maxChild] > elements[root])
		{
			swap(elements[maxChild], elements[root]);
			ReheapDown_re(maxChild, bottom);
		}
	}
}

Iterative

template<class ItemType>
void HeapType<ItemType>::ReheapDown(int root, int bottom)
{
	int maxChild, leftChild, rightChild;
	bool reheaped = false;
	leftChild = root * 2 + 1;
	while (leftChild <= bottom && !reheaped) {
		if (leftChild == bottom)
			maxChild = leftChild;
		else {
			rightChild = root * 2 + 2;
			maxChild = (elements[leftChild] <= elements[rightChild]) ? elements[rightChild] : elements[leftChild];
		}
		if (elements[root] < elements[maxChild]) {
			Swap(elements[root], elements[maxChild]);
			root = maxChild;
			leftChild = root * 2 + 1;
		}
		else
			reheaped = true;
	}
}

maxChild: root 기준 child node 중에 최대값을 가진 node의 위치
elements[leftChild] == elements[bottom]: root가 하나의 child node만 가지는 경우
ReHeapDown(maxChild, bottom): swap된 위치 기준으로 위에서 Heap을 깼던 item이 바뀐 위치에서도 Heap을 깨고 있을 경우 다시 정렬

ReHeapUp

node를 insert 했을 때 Array의 마지막에 삽입되는데, 새로운 node 때문에 Heap이 깨짐
child 중 right most (가장 오른쪽에 있는 item) 때문에 Heap이 깨지는 경우
Heap을 깨는 item을 root 방향으로 올림
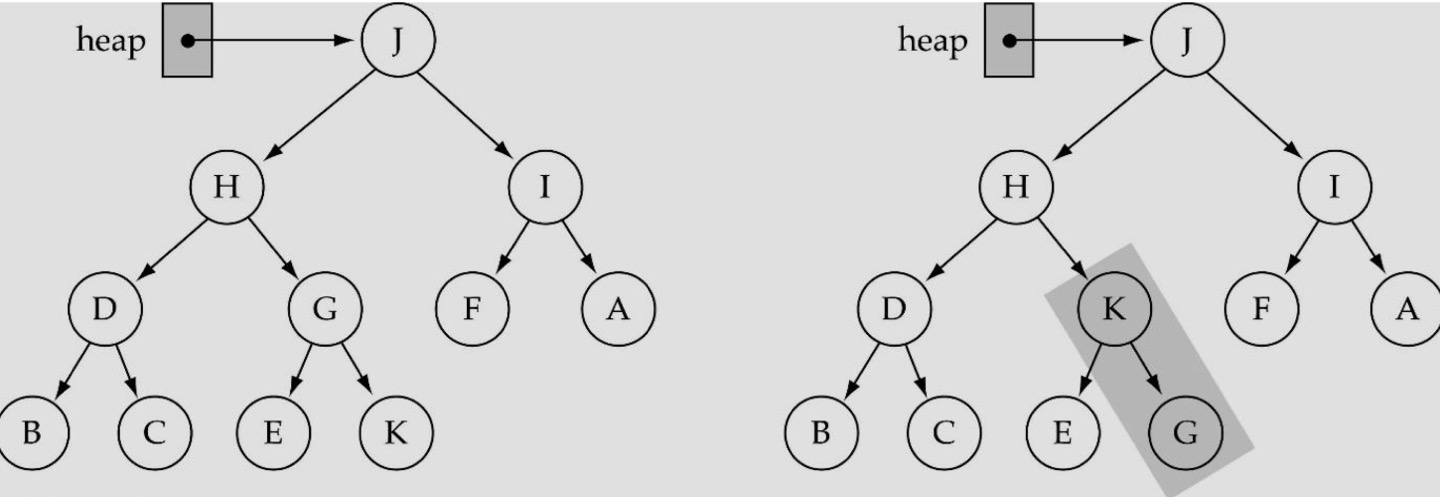
Recursive

template<class ItemType>
void HeapType<ItemType>::ReheapUp(int root, int bottom)
{
	int parent;

	if (bottom > root)
	{
		parent = (bottom - 1) / 2;
		if (elements[parent] < elements[bottom])
		{
			swap(elements[parent], elements[bottom]);
			ReheapUp(root, parent);
		}
	}
}

Iterative

template<class ItemType>
void HeapType<ItemType>::ReheapUp(int root, int bottom)
{
	int parent;
	bool reheaped = false;

	while (bottom > root && !reheaped) {
		parent = (bottom - 1) / 2;
		if (elements[parent] < elements[bottom]) {
			Swap(elements[parent], elements[bottom]);
			bottom = parent;
		}
		else
			reheaped = true;
	}
}

DeleteItem

Heap의 가장 마지막 아이템 (right most item)을 삭제하려는 item의 위치에 덮어씀
Heap의 마지막 아이템 삭제
삭제하려는 item의 위치에 덮어씌워진 heap의 right most item 때문에 위에서 heap이 깨짐
ReHeapDown

InsertItem

새로운 item을 Heap의 가장 마지막에 넣어 줌
새로 넣은 item 때문에 아래에서 Heap이 깨짐
ReHeapUp

Graphs

graph = (Vertex, Edge)의 튜플
- Vertex: 노드
- Edge: 연결
Ected graph
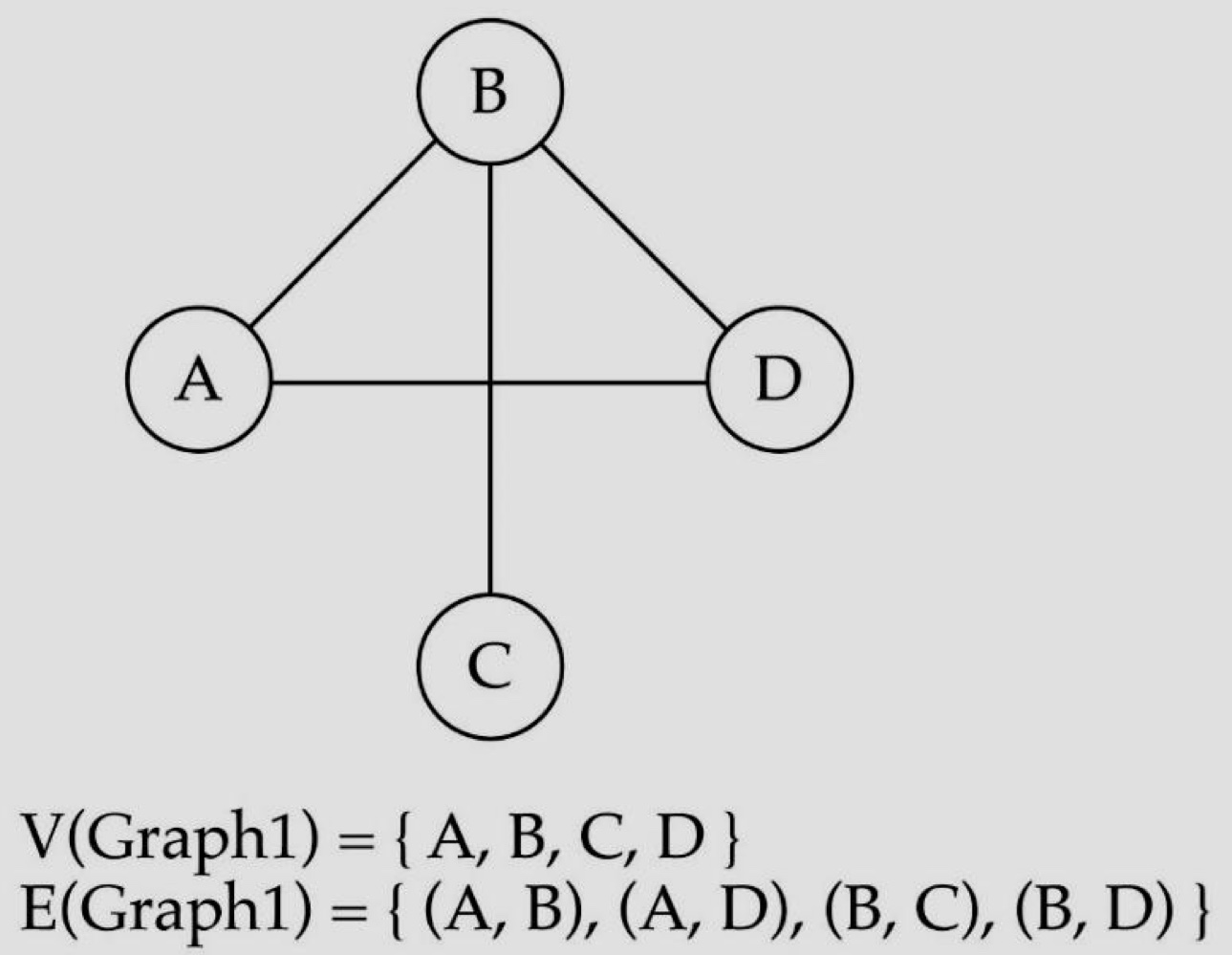
- edge(연결)끼리의 방향성이 존재하지 않는 graph
Directed graph
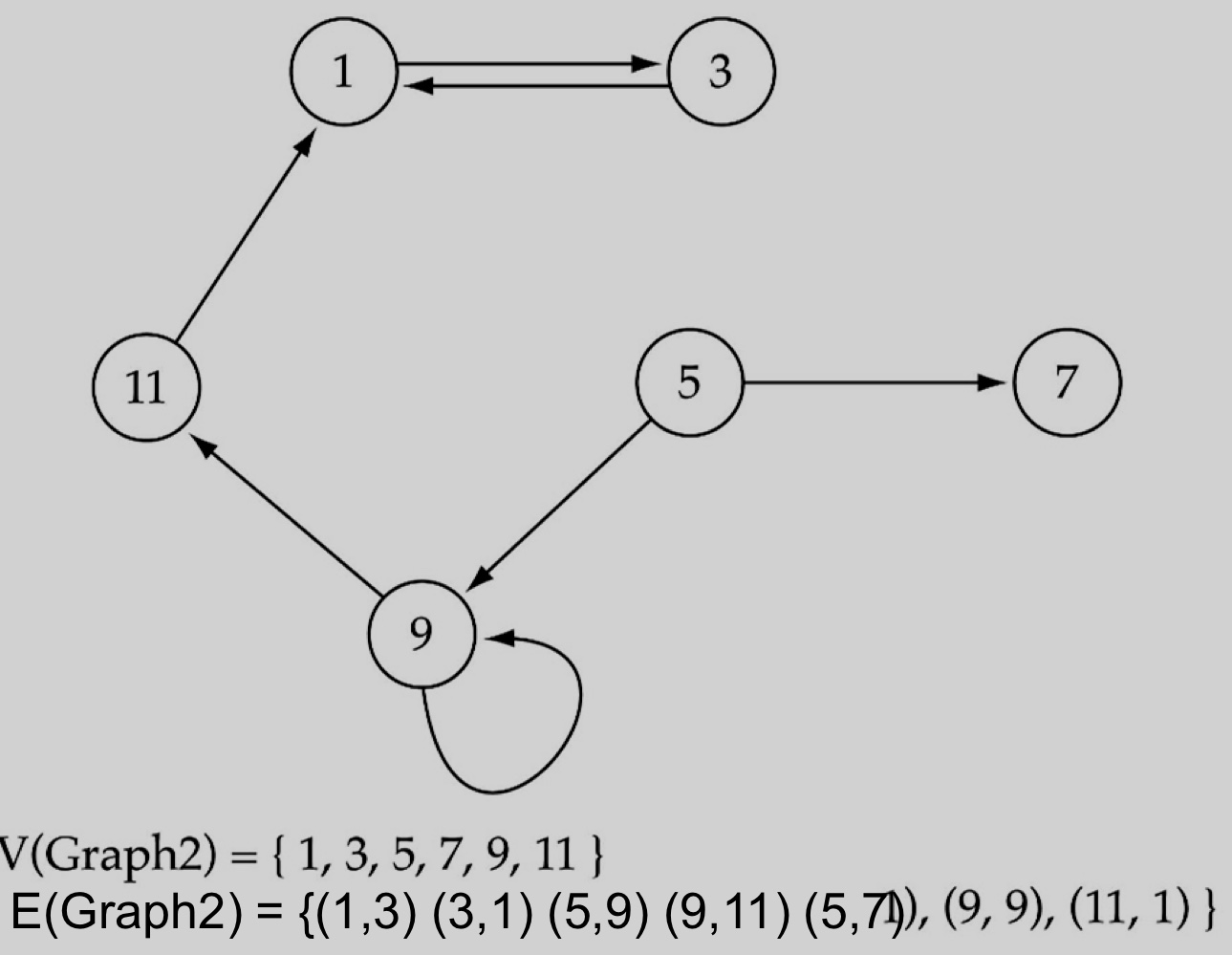
- edge(연결)끼리의 방향성이 존재하는 graph
Tree는 graph의 특이 케이스 중 하나

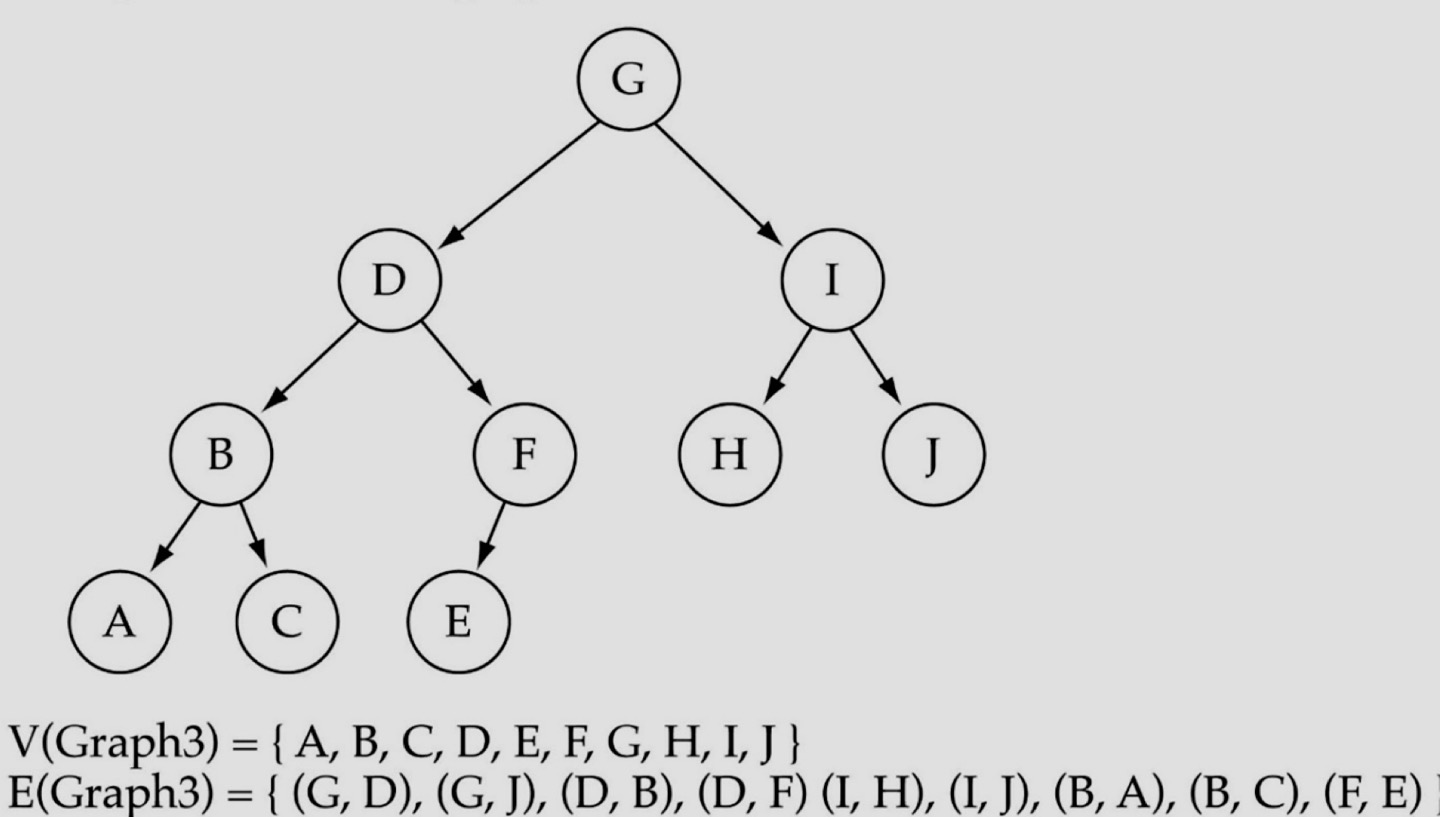
Terminology

Adjacent node: edge로 연결된 이웃 노드
Path: node A에서 node B로 갈 때 지나가는 vertex들의 집합 (순서를 가짐)
Complete graph: 어떤 vertex 쌍을 골라도 edge가 존재하는 graph
- Ected일 경우 연결만 존재하면 됨
  - nC2개의 edge 존재 n * (n-1) / 2
- Directed일 경우 양방향으로 존재
  - nP2개의 edge 존재 n * (n-1)
Weighted graph: edge마다 weight 존재해서 중요도를 다르게 부여한 graph

Graph Implementation

Adjacency Matrix: Array 기본으로 구현
- Vertices: Vertex에 해당하는 index를 알려 주는 1차원 배열
- Adjacency Matrix: Vertex끼리의 edge 존재 유무와 weight를 알려 주는 2차원 배열
- Array Based이기 때문에 충분한 크기를 설정해 둬야 함
- Vertices의 index를 정렬해 놓으면 Searching 시간을 줄일 수 있음
  - Sorted O(logN), Unsorted O(N)
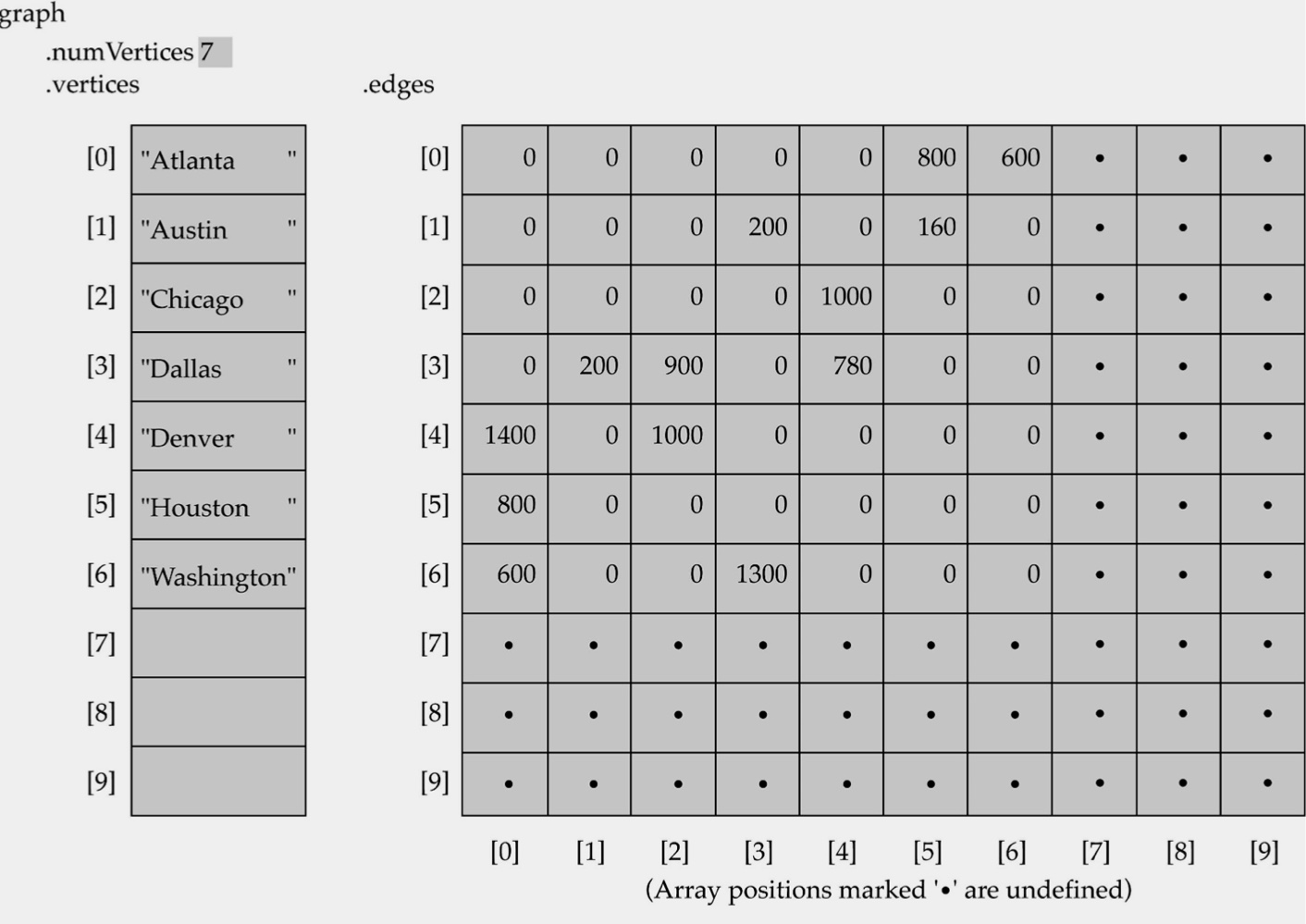
Adjacency List: Linked-List로 구현
- Vertices: Vertex에 해당하는 index를 알려 주는 1차원 배열
- Vertex list: Vertex 마다 edge로 연결된 다른 노드들을 Linked list로 표현
  - 해당 노드에서 뻗어나가는 edge만
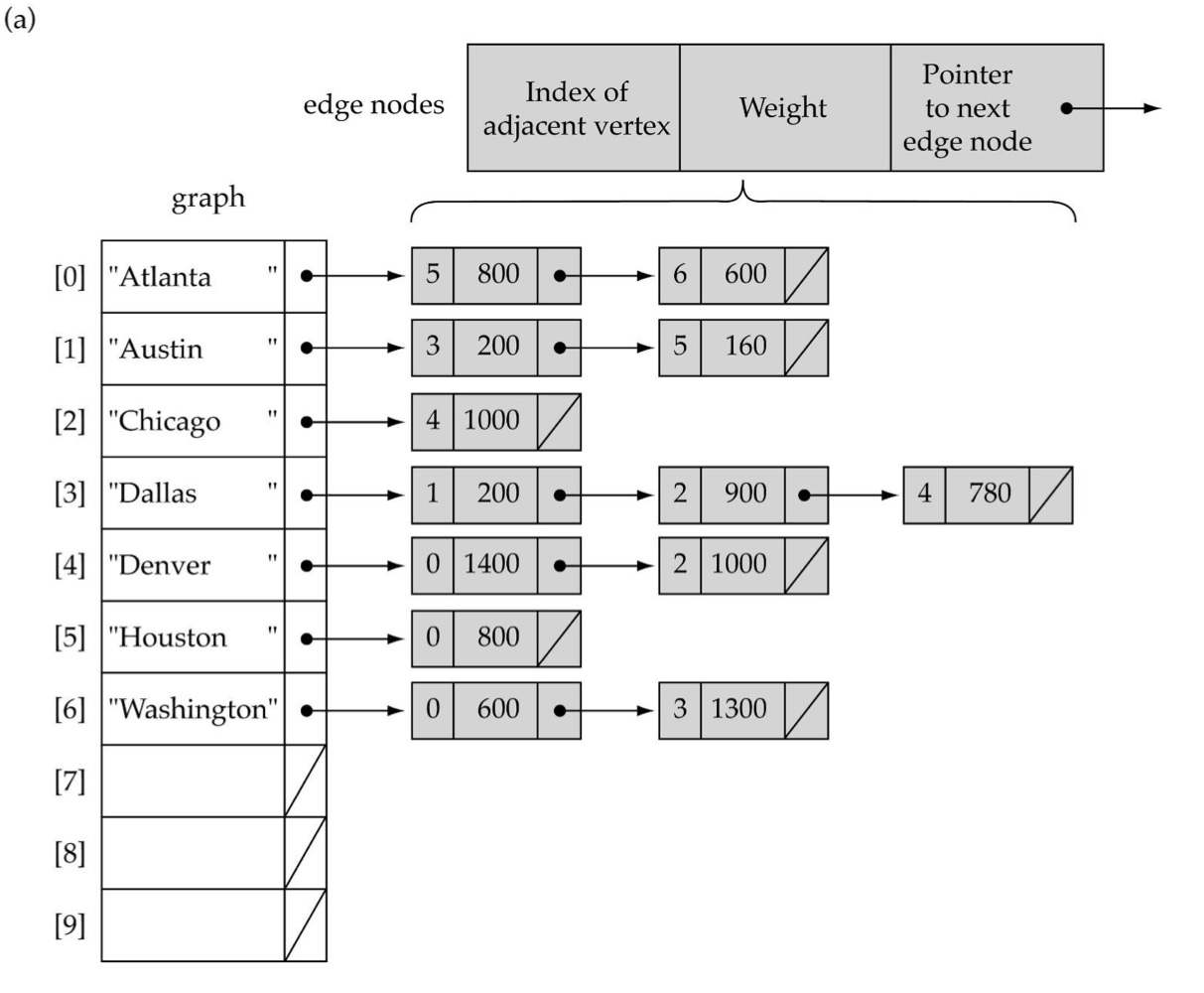
Compare
- Adjacency Graph
  - dense한 graph에 효과적
  - vertex에 비해 edge가 적으면 adjacency matrix 메모리를 많이 낭비하기 때문
  - 두 node 사이의 연결성을 빠르게 찾을 수 있음
  - Memory = Vertex (N) + Adjacency Matrix (N^2) = N^2
- Adjacency List
  - sparse한 graph에 효과적
  - vertex에 연결된 edge가 많을수록 edge node라는 공간을 쓸데없이 많이 잡기 때문
  - 한 Vertex에 연결된 다른 Vertex를 빠르게 찾을 수 있음
  - Memory = Vertex (N) + Adjacency List (N) = N

Adjacency Matrix Graph

Adjacency Matrix Graph ADT

template<class VertexType>
class GraphType
{
public:
	GraphType();             
	GraphType(int maxV);         
	~GraphType();
	void AddVertex(VertexType vertex);
	void AddEdge(VertexType fromVertex, VertexType toVertex, int weight);
	int WeightIs(VertexType fromVertex, VertexType toVertex);
	void ClearMarks();
	bool IsMarked(VertexType vertex);
	void MarkVertex(VertexType vertex);
	void GetToVertices(VertexType vertex, QueType<VertexType>& adjVertices);
private:
	int numVertices;
	int maxVertices;
	VertexType* vertices;
	int edges[50][50];
	bool* marks;
};

Constructor
- vertices라는 vertex 저장하는 1차원 array 생성

template<class VertexType>
GraphType<VertexType>::GraphType()
{
	numVertices = 0;
	maxVertices = 50;
	vertices = new VertexType[50];
	marks = new bool[50];
}

Destructor
- for 문 돌면서 vertex에 해당하는 edge들도 삭제

template<class VertexType>
GraphType<VertexType>::~GraphType()
{
	delete[] vertices;
	for (int i - 0; i < maxVertices; i++)
		delete[] edges[i];
	delete[] marks;
}

AddVertex
- vertex array에 새로운 vertex 넣어 주기
- 새로운 vertex와 연결된 edge는 모두 NULL 값으로 초기화
- numVertices 수 1 증가

template<class VertexType>
void GraphType<VertexType>::AddVertex(VertexType vertex)
{
	vertices[numVertices] = vertex;

	for (int index = 0; index < numVertices; index++)
	{
		edges[numVertices][index] = NULL_EDGE;
		edges[index][numVertices] = NULL_EDGE;
	}
	numVertices++;
}

AddEdges
- IndexIs: vertex의 index 정보를 저장하는 1차원 배열 vertices와 찾고자 하는 vertex 정보를 입력하면 해당 vertex의 index를 반환해 주는 함수
- row에는 edge가 뻗어나가는 vertex index 저장
- col에는 edge가 들어오는 vertex index 저장
- adjacenct matrix에서 row, col 위치에 해당하는 곳에 edge 삽입

template<class VertexType>
int IndexIs(VertexType* vertices, VertexType vertex)
{
	int index = 0;

	while (!(vertex == vertices[index]))
		index++;
	return index;
}

template<class VertexType>
void GraphType<VertexType>::AddEdge(VertexType fromVertex, VertexType toVertex, int weight)
{
	int row;
	int col;

	row = IndexIs(vertices, fromVertex);
	col = IndexIs(vertices, toVertex);
	edges[row][col] = weight;
}

WeightIs
- IndexIs: vertex의 index 정보를 저장하는 1차원 배열 vertices와 찾고자 하는 vertex 정보를 입력하면 해당 vertex의 index를 반환해 주는 함수
- row에는 edge가 뻗어나가는 vertex index 저장
- col에는 edge가 들어오는 vertex index 저장
- adjacenct matrix에서 row, col 위치에 해당하는 곳의 edge 반환

template<class VertexType>
int GraphType<VertexType>::WeightIs (VertexType fromVertex, VertexType toVertex)
{
	int row;
	int col;

	row = IndexIs(vertices, fromVertex);
	col = IndexIs(vertices, toVertex);
	return edges[row][col];
}

ClearMarks
- travel 시에 방문했는 기록을 남기는 marks Array 초기화

template<class VertexType>
void GraphType<VertexType>::ClearMarks()
{
	for (int i = 0; i < numVertices; i++)
		marks[i] = false;
}

IsMarked
- 해당 vertex가 방문한 기록이 있는지 물어보는 메소드

template<class VertexType>
bool GraphType<VertexType>::IsMarked(VertexType vertex)
{
	index = IndexIs(vertices, vertex);
	return (marks[index] == true);
}

MarkVertex
- 해당 vertex를 방문했다고 기록하는 메소드

template<class VertexType>
void GraphType<VertexType>::MarkVertex(VertexType vertex)
{
	index = IndexIs(vertices, vertex);
	marks[index] = true;
}

GetToVertices
- vertex에서 뻗어나간 edge랑 연결된 vertex를 adjVertices에 Enqueue하는 메소드

template<class VertexType>
void GraphType<VertexType>::GetToVertices(VertexType vertex, QueType<VertexType>& adjVertices)
{
	int fromIndex;
	int toIndex;

	fromIndex = IndexIs(vertices, vertex);
	for (toIndex = 0; toIndex < numVertices; toIndex++)
		if (edges[fromIndex][toIndex] != NULL_EDGE)
			adjVertices.Enqueue(vertices[toIndex]);
}

Adjacency List

Graph Searching

DFS (Depth-First-Search)

가장 깊이 있는 노드부터 travel하는 방법
stack으로 구현 가능
원하는 것 찾을 때까지 stack에서 Pop
Pop method 결과로 나온 item과 직접 연결된 node들 다시 push
stack의 last in, first out 방식이 가장 얕은 곳에 있는 item이 먼저 pop 되도록 해 줌

template<class VertexType>
void GraphType<VertexType>::DepthFirstSearch(VertexType startVertex, VertexType endVertex)
{
	StackType<VertexType> stack;
	QueType<VertexType> vertexQ;
	bool found = false;
	VertexType vertex;
	VertexType item;

	ClearMarks();
	stack.Push(startVertex);

	while (!stack.IsEmpty() && !found)
	{
		stack.Pop(vertex);
		if (vertex == endVertex)
		{
			std::cout << vertex << std::endl;
			found = true;
		}
		else
		{
			if (!IsMarked(vertex))
			{
				MarkVertex(vertex);
				std::cout << vertex << std::endl;
				GetToVertices(vertex, vertexQ);
				while (!vertexQ.IsEmpty())
				{
					vertexQ.Dequeue(item);
					if (!IsMarked(item))
						stack.Push(item);
				}
			}
		}
	}
	if (!found)
		std::cout << "Path not found." << std::endl;
}

BFS (Breadth-First-Search)

same depth를 다 둘러보고 다음 level의 노드들을 살피는 travel 방식
queue로 구현 가능
원하는 것 찾을 때까지 queue에서 Dequeue
Dequeue의 결과로 나온 item과 직접 연결된 node들 다시 Enqueue
queue의 first in, first out 방식이 같은 depth에 있는 item들부터 나오도록 해 줌

template<class VertexType>
void GraphType<VertexType>::BreathFirstSearch(VertexType startVertex, VertexType endVertex)
{
	QueType<VertexType> queue;
	QueType<VertexType> vertexQ;

	bool found = false;
	VertexType vertex;
	VertexType item;

	ClearMarks();
	queue.Enqueue(startVertex);

	while (!queue.IsEmpty() && !found)
	{
		queue.Dequeue(vertex);

		if (vertex == endVertex)
		{
			std::cout << vertex << std::endl;
			found = true;
		}
		else
		{
			if (!IsMarked(vertex))
			{
				MarkVertex(vertex);
				std::cout << vertex << std::endl;
				GetToVertices(vertex, vertexQ);

				while (!vertexQ.IsEmpty())
				{
					vertexQ.Dequeue(item);
					if (!IsMarked(item))
						queue.Enqueue(item);
				}
			}
		}
	}
	if (!found)
		std::cout << "Path not found." << std::endl;
}

LAP

DeleteEdge

Edge를 삭제해 주는 method

template<class VertexType>
void GraphType<VertexType>::DeleteEdge(VertexType fromVertex, VertexType toVertex)
{
	int row;
	int col;
	row = IndexIs(vertices, fromVertex);
	col = IndexIs(vertices, toVertex);
	edges[row][col] = NULL_EDGE;
}

DepthFirstSearch_Recursive

stack을 사용하지 않고 재귀적 방법으로 DFS 하는 방법
base case: 시작 위치와 종료 위치가 같을 때
vertexQ에 시작 위치와 연결된 노드들 Enqueue
하나씩 Dequeue하여 startVertex와 비교 (Marked 검사)
같지 않을 경우 꺼낸 item을 start로 하여 DFS 실행

template<class VertexType>
bool GraphType<VertexType>::DepthFirstSearch_re(VertexType startVertex, VertexType endVertex)
{
	QueType<VertexType> vertexQ;
	VertexType vertex;

	if (startVertex == endVertex)
	{
		std::cout << endVertex << std::endl;
		return true;
	}

	GetToVertices(startVertex, vertexQ);
	while (!vertexQ.IsEmpty())
	{
		vertexQ.Dequeue(vertex);
		if (vertex != startVertex)
		{
			if (DepthFirstSearch_re(vertex, endVertex))
			{
				std::cout << startVertex << std::endl;
				return true;
			}
		}
		else
			continue;
	}
	return false;
}

PP

Max_Heap

class HeapType:
    elements = []
    numElemnents = 0

    def ReHeapUp(self, root, bottom):
        reheaped = False
        while(bottom > root and not reheaped):
            parent = (bottom - 1) / 2
            if (self.elements[parent] < self.elements[bottom]):
                self.elements[parent], self.elements[bottom] = self.elements[bottom], self.elements[parent]
                bottom = parent
            else:
                reheaped = True

    def ReHeapDown(self, root, bottom):
        reheaped = False
        leftChild = root * 2 + 1

        while(leftChild <= bottom and not reheaped):
            if(leftChild == bottom):
                maxChild = leftChild
            else:
                rightChild = root * 2 + 2
                if (self.elements[leftChild] <= self.elements[rightChild]):
                    maxChild = rightChild
                else:
                    maxChild = leftChild
            if(self.elements[root] < self.elements[maxChild]):
                self.elements[root], self.elements[maxChild] = self.elements[maxChild], self.elements[root]
                root = maxChild
                leftChild = root * 2 + 1
            else:
                reheaped = True

Min_Heap

class HeapType:
    elements = []
    numElemnents = 0

    def ReHeapUp(self, root, bottom):
        reheaped = False
        while(bottom > root and not reheaped):
            parent = (bottom - 1) / 2
            if (self.elements[parent] > self.elements[bottom]):
                self.elements[parent], self.elements[bottom] = self.elements[bottom], self.elements[parent]
                bottom = parent
            else:
                reheaped = True

    def ReHeapDown(self, root, bottom):
        reheaped = False
        leftChild = root * 2 + 1

        while(leftChild <= bottom and not reheaped):
            if(leftChild == bottom):
                minChild = leftChild
            else:
                rightChild = root * 2 + 2
                if (self.elements[leftChild] >= self.elements[rightChild]):
                    minChild = rightChild
                else:
                    minChild = leftChild
            if(self.elements[root] > self.elements[minChild]):
                self.elements[root], self.elements[minChild] = self.elements[minChild], self.elements[root]
                root = minChild
                leftChild = root * 2 + 1
            else:
                reheaped = True

PQType

from Max_Heap import *

MAX_ITEMS = 100

class PQType():
    def __init__(self):
        self.items = HeapType()
        self.length = 0
    
    def make_empty(self):
        self.length = 0

    def enqueue(self, newitem):
        if(not self.length == MAX_ITEMS):
            self.length += 1
            self.items.elements[self.length-1] = newitem
            self.items.ReHeapUp(0, self.length-1)
    
    def dequeue(self):
        if(not self.length == 0):
            item = self.items.elements[0]
            self.items.elements[0] = self.items.elements[self.length-1]
            self.length -= 1
            self.items.ReHeapDown(0, self.length -1)
            return item
    
    def is_full(self):
        return self.length == MAX_ITEMS

    def is_empty(self):
        return self.length == 0

Graph

from QueType import *
from StackType import *

NULL_EDGE = 0

def index_is(vertices, vertex):
    index = 0

    while index < len(vertices) and vertex != vertices[index]:
        index += 1

    if not index < len(vertices):
        return -1
    else:
        return index

class GraphType:
    def __init__(self, maxV=50):
        self.numVertices = 0
        self.maxVertices = maxV
        self.vertices = [None] * maxV
        self.edges = [[NULL_EDGE] * maxV for _ in range(maxV)]
        self.marks = [None] * maxV

    def add_vertex(self, vertex):
        self.vertices[self.numVertices] = vertex
        for index in range(self.numVertices):
            self.edges[self.numVertices][index] = NULL_EDGE
            self.edges[index][self.numVertices] = NULL_EDGE
        self.numVertices += 1

    def add_edge(self, fromVertex, toVertex, weight):
        row = index_is(self.vertices, fromVertex)
        col = index_is(self.vertices, toVertex)
        self.edges[row][col] = weight


    def weight_is(self, fromVertex, toVertex):
        row = index_is(self.vertices, fromVertex)
        col = index_is(self.vertices, toVertex)
        return self.edges[row][col]


    def get_to_vertices(self, vertex, adjVertices):
        fromIndex = index_is(self.vertices, vertex)
        for toIndex in range(self.numVertices):
            if(self.edges[fromIndex][toIndex] != NULL_EDGE):
                adjVertices.enqueue(self.vertices[toIndex])


    def clear_marks(self):
        for index in range(self.numVertices):
            self.marks[index] = False


    def is_marked(self, vertex):
        index = index_is(self.vertices, vertex)
        return self.marks[index]


    def mark_vertex(self, vertex):
        index = index_is(self.vertices, vertex)
        self.marks[index] = True


    def delete_edge(self, fromVertex, toVertex):
        row = index_is(self.vertices, fromVertex)
        col = index_is(self.vertices, toVertex)
        self.edges[row][col] = NULL_EDGE

DepthFistSearch

from GraphType import *

def depth_first_search(graph, startVertex, endVertex):
    stack = StackType()
    vertexQ = QueType()
    found = False
    graph.clear_marks()
    stack.push(startVertex)

    while(not stack.is_empty() and not found):
        vertex = stack.top()
        stack.pop()
        if(vertex == endVertex):
            print(endVertex)
            found = True
        else:
            if(not graph.is_marked(vertex)):
                graph.mark_vertex(vertex)
                print(vertex)
                graph.get_to_vertices(vertex, vertexQ)

                while(not vertexQ.is_empty()):
                    item = vertexQ.dequeue()
                    if(not graph.is_marked(item)):
                        stack.push(item)
    if(not found):
        print("Path not found.")

BreathFirstSearch

from GraphType import *

def breadth_first_search(graph, startVertex, endVertex):
    queue = QueType()
    vertexQ = QueType()
    found = False
    graph.clear_marks()
    queue.enqueue(startVertex)

    while(not queue.is_empty() and not found):
        vertex = queue.dequeue()
        if(vertex == endVertex):
            print(endVertex)
            found = True
        else:
            if(not graph.is_marked(vertex)):
                graph.mark_vertex(vertex)
                print(vertex)
                graph.get_to_vertices(vertex, vertexQ)

                while(not vertexQ.is_empty()):
                    item = vertexQ.dequeue()
                    if(not graph.is_marked(item)):
                        queue.enqueue(item)
    if(not found):
        print("Path not found.")

Huisu

이전 포스트

CH 08 Binary Search Tree

다음 포스트

CH 9 Priority Queues, Heaps, and Graphs

DataStructure

Priority Queues

Priority Queue

Implementation Level

PQType.h

PQType Method

PQType.cpp

Time Complexcity

Heaps

Heap

ReHeapDown

ReHeapUp

DeleteItem

InsertItem

Graphs

Graphs

Terminology

Graph Implementation

Adjacency Matrix Graph

Adjacency List

Graph Searching

DFS (Depth-First-Search)

BFS (Breadth-First-Search)

LAP

DeleteEdge

DepthFirstSearch_Recursive

PP

Max_Heap

Min_Heap

PQType

Graph

DepthFistSearch

BreathFirstSearch

CH 08 Binary Search Tree

CH 10 Sorting and Searching Algorithm

0개의 댓글