
Simple Sorting
Sorting
- 비교 가능한 element끼리 정렬
- ascending: 오름차순
- descending: 내림차순
- 비교 대상인 key 값은 비교 가능하고 unique해야 함
Straight Selection Sorting
- 배열을 정렬된 부분과 정렬되지 않은 부분으로 나눔
- 정렬되지 않은 부분에서 가장 작은 애랑 자리 Swap
- 바꾼 자리 다음부터 위 작업 반복
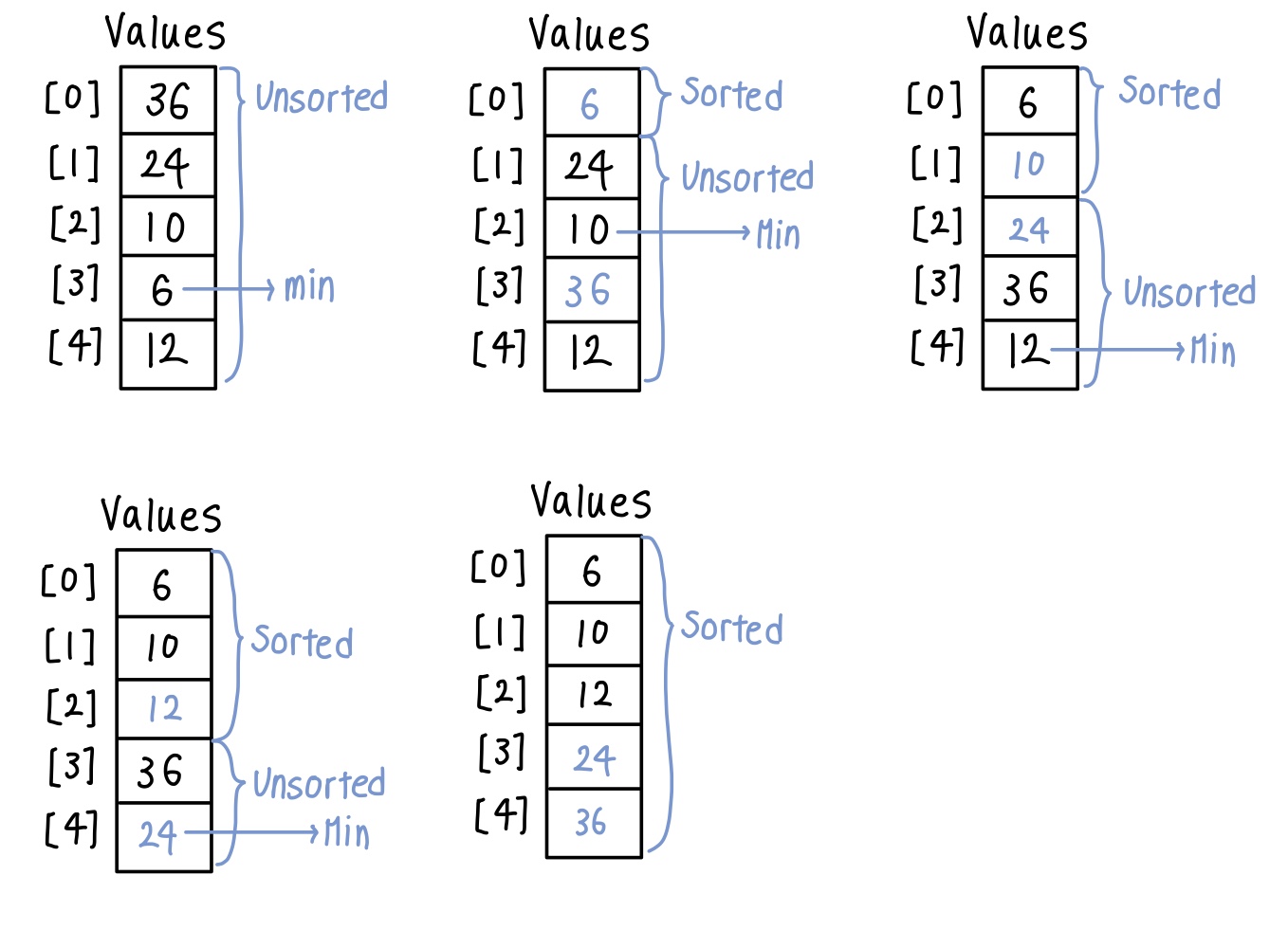
- N개의 item이 존재할 때 n*(N-1) / 2 번 비교
- 계산 복잡도 O(N^2)
int minIndex(ItemType values[], int start, int end)
{
int indexOfMin = start;
for (int index = start + 1; index <= end; index++)
{
if (values[index] < values[indexOfMin])
indexOfMin = index;
}
return indexOfMin
}
template<class ItemType>
void SelectionSort(ItemType values[], int numValues)
{
int endIndex = numValues - 1;
for (int current = 0; current < endIndex; current++)
{
Swap(values[current], values[minIndex(values, current, endIndex)]);
}
}Bubble Sort
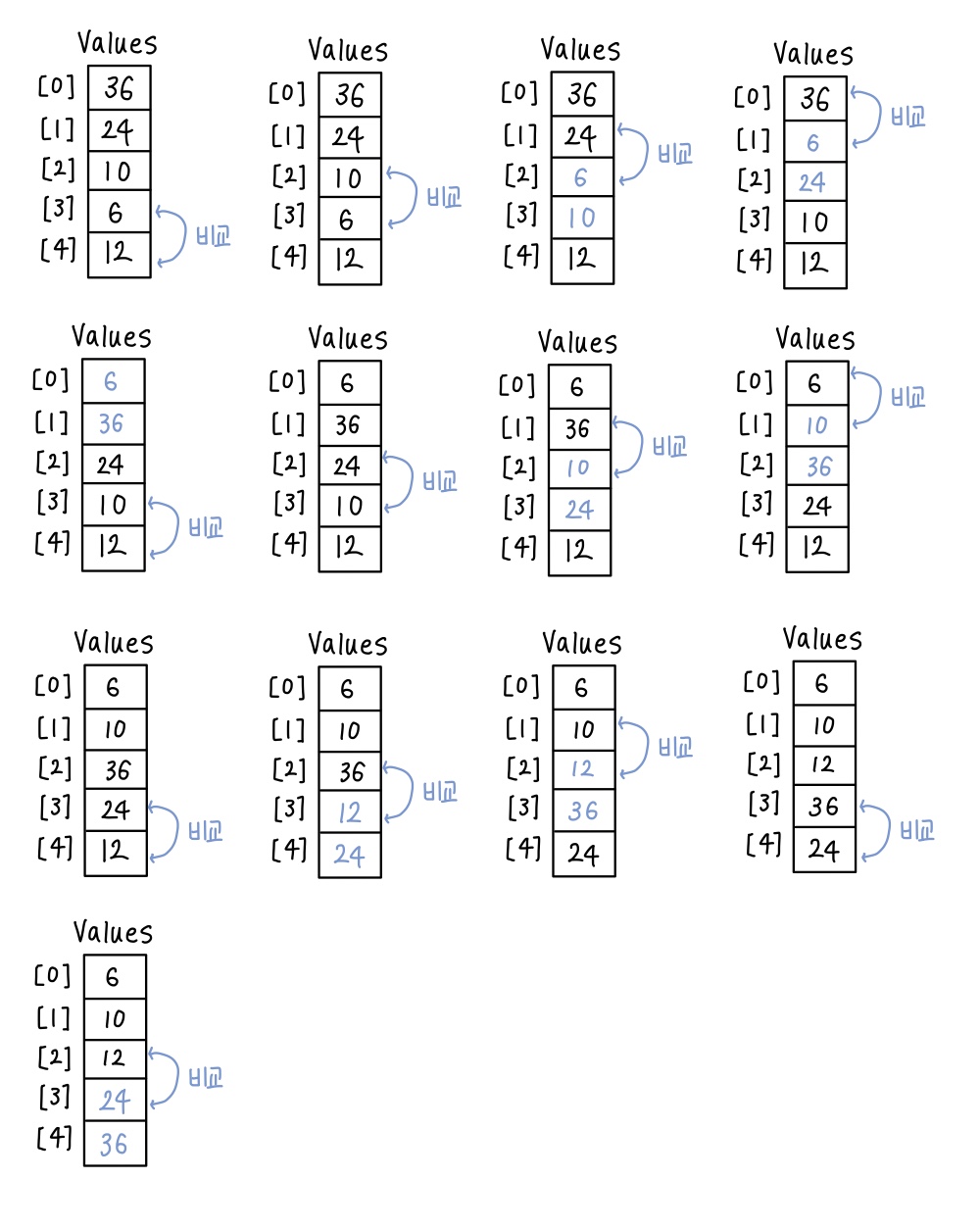
- 이웃 노드랑 비교해서 잘못된 위치가 있다면 하나씩 위치 swap
- 바른 위치에 갈수 있도록 하나하나씩 조정해 나가는 방식
- item 하나당 N 번씩 bubble 이동
- O(N)
template<class ItemType>
void BubbleUp(ItemType values[], int startIndex, int endIndex)
{
for (int index = endIndex; index > startIndex; index--)
{
if (values[index] > values[index - 1])
Swap(values[index], values[index - 1]);
}
}
template<class ItemType>
void BubbleSort(ItemType values[], int numValues)
{
int current = 0;
while (current < numValues - 1)
{
BubbleUp(values, current, numValues - 1);
current++;
}
}Insertion Sort
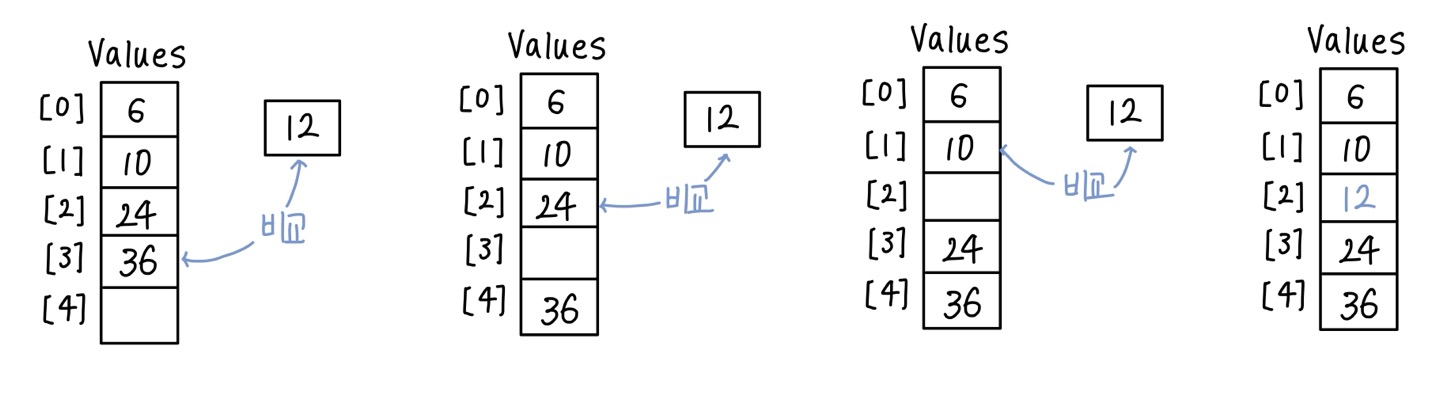
- 구조를 만들 때부터 Sorting된 상태로 생성하는 방법
- 끝부터 시작해서 insert하는 새로운 item의 위치를 찾을 때까지 공간을 하나씩 밀어내는 방법
- item 하나에 N 번씩 비교
- O(N^2)
template<class ItemType>
void InsertItem(ItemType values[], int start, int end)
{
bool finished = false;
int current = end;
bool moreToSearch = (current != start);
while (moreToSearch && !finished)
{
if (values[current] < values[current - 1])
{
Swap(values[current], values[current - 1]);
current--;
moreToSearch = (current != start);
}
else
finished = true;
}
}
template<class ItemType>
void InsertionSort(ItemType values[], int numValues)
{
for (int count = 0; count < numValues; count++)
InsertItem(values, 0, count);
}Complex Sorting
Heap Sort
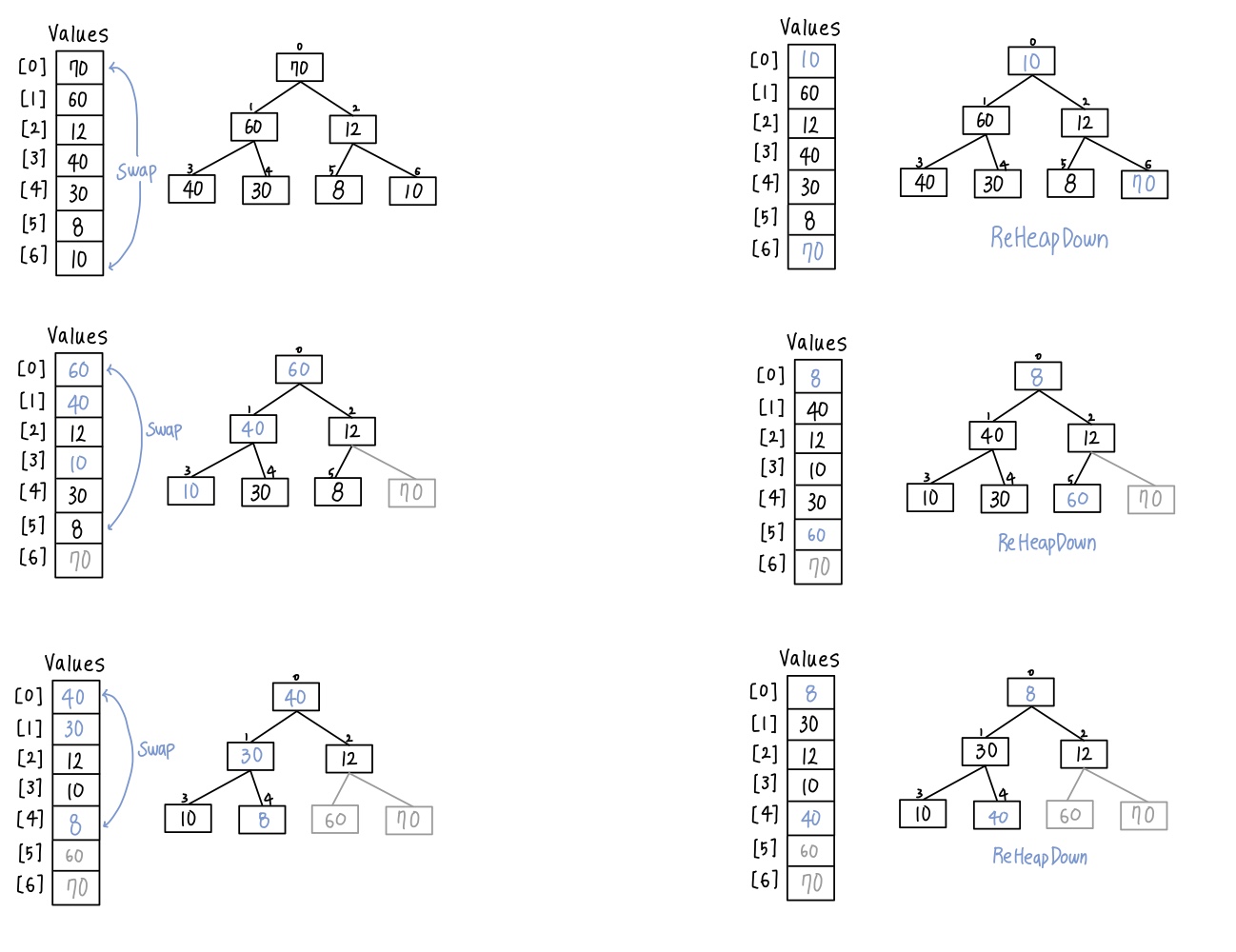
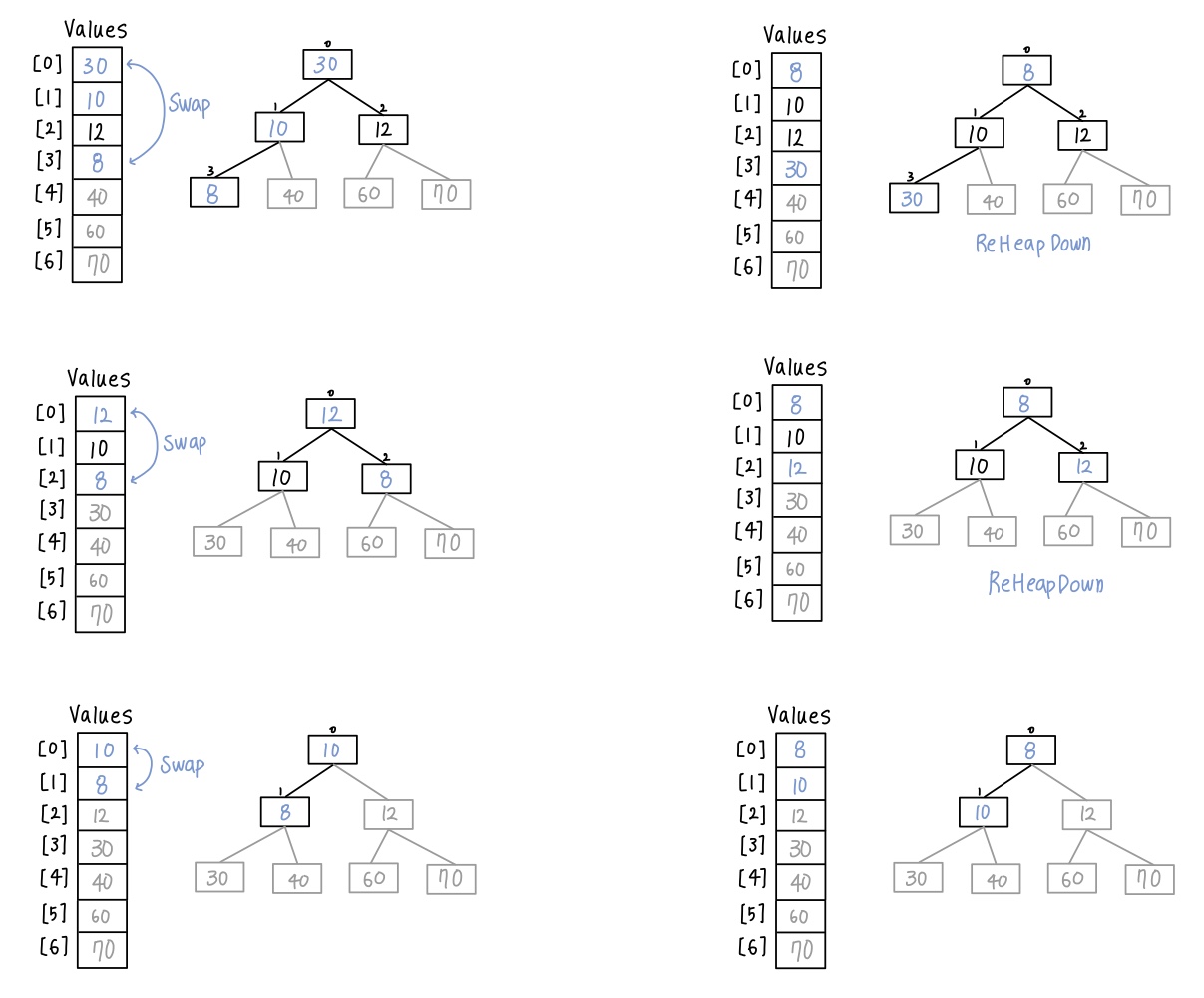
- 정렬되지 않은 구조체들을 Heap으로 만든 다음 root부터 하나씩 꺼냄
- Max Heap: 자기 자신의 child node보다 항상 크거나 같은 값을 갖는 complete tree
- Min Heap: 자기 자신의 child node보다 항상 작거나 같은 값을 갖는 complete tree
- root 부터 꺼낸 뒤 ReHeapDown으로 Heap 유지
- 정렬되지 않은 구조체 heap으로 만들기
- Leaf node는 이미 Heap이기 때문에 위로 하나씩 타고 올라가면서 Heap 모양 만들어 주기
- Non Leaf node의 수 = N/2 - 1
- Time Complexity
- ReHeapDown = O(logN)
- Heap 만들기 = N/2 * logN
- root부터 꺼내서 정렬하기 = N * logN
- 총 알고리즘 O(N * logN)
template<class ItemType>
void HeapSort(ItemType values[], int numValues)
{
// leaf node가 아닌 곳부터 heap으로 만들어 줌
for (int index = numValues / 2 - 1; index >= 0; index--)
{
ReheapDown(values, index, numValues - 1);
}
for (int index = numVales - 1; index > 0; index--)
{
Swap(values[0], values[index]);
ReheapDown(values, 0, index-1);
}
}Quick Sort
- pivot을 중심으로 pivot 앞에는 pivot보다 작은 item, pivot 뒤에는 pivot보다 큰 item으로 나누는 과정을 반복하는 정렬 방식
- Devided Conquar
- 핸들링할 수 있는 수준까지 잘라서 해결
- Time Complexcity
- 이상적으로 반씩 쪼갰을 때
- pivot을 지정하고 split을 실행하는 것 logN 시행
- split이 시행될 때마다 pivot 기준으로 자리를 재배열하는 과정에서 N 소요
- 총 O(N * logN)
- pivot을 지정하고 split을 실행하는 것 logN 시행
- 이미 정렬돼 있는 요소를 정렬했을 때
- split 후 반환되는 splitPoint가 정렬 순서로 나오기 때문에 split N번 실행
- split이 실행될 때마다 pivot과 값 N 번 비교
- 총 O(N^2)
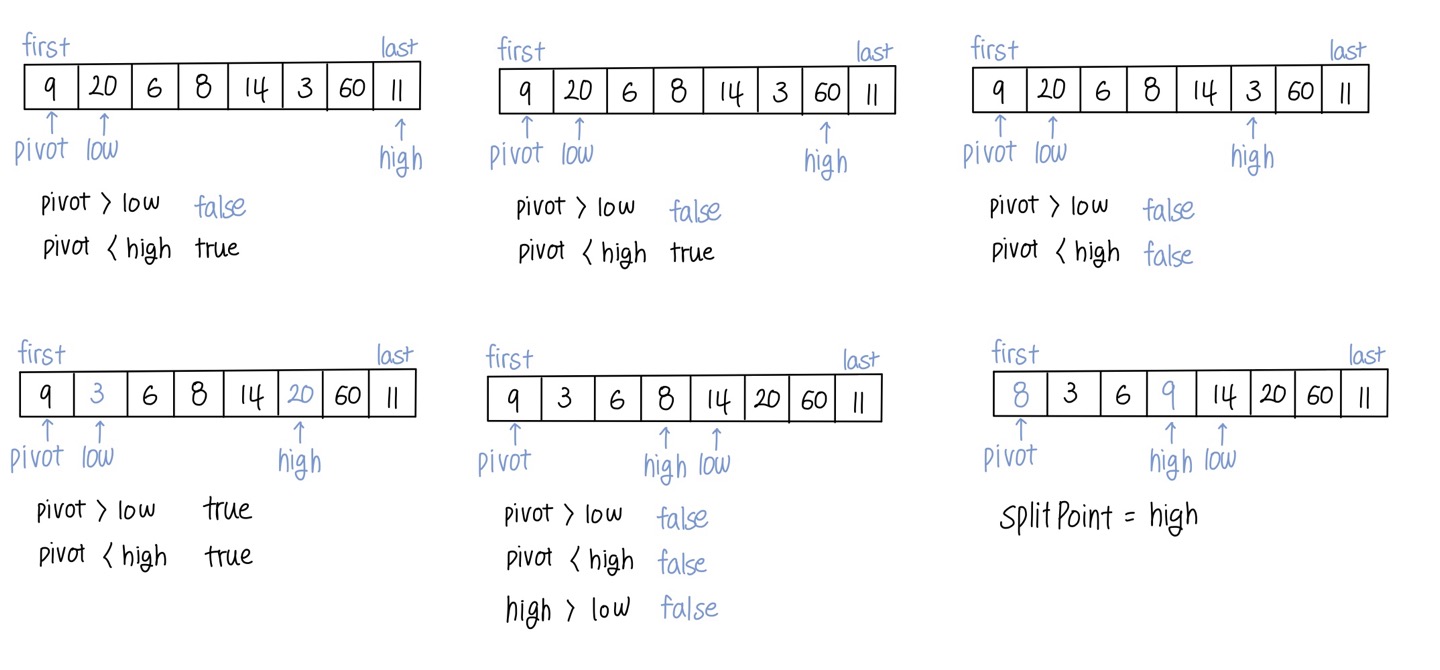
- 이상적으로 반씩 쪼갰을 때
int Split(int values[], int first, int last) {
int pivot, temp;
int low, high;
low = first + 1;
high = last;
pivot = values[first];
while (low < high) {
while (low <= last && values[low] < pivot)
low++;
while (high >= first && values[high] > pivot)
high--;
if (low < high) {
temp = values[low];
values[low] = values[high];
values[high] = temp;
}
}
temp = values[first];
values[first] = values[high];
values[high] = temp;
return high;
}
void QuickSort(int values[], int first, int last) {
if (first < last) {
int splitPoint = Split(values, first, last);
QuickSort(values, first, splitPoint - 1);
QuickSort(values, splitPoint + 1, last);
}
}Merge Sort
- 반씩 잘라서 오른쪽 sorting, 왼쪽 sorting
- 한 개나 두 개의 item만 남을 때까지 쪼개서 병합
- Devided Conquar
- 쪼갠 뒤 다시 합치는 Merge 함수 필요
- 새로운 버퍼를 만들어서 작은 item부터 넣어 합침
- 메모리를 많이 사용하는 알고리즘
- Time Complexcity
- 반씩 쪼개는 작업 logN
- 다시 Copying Back 하는 작업 N
- 총 O(N * logN)
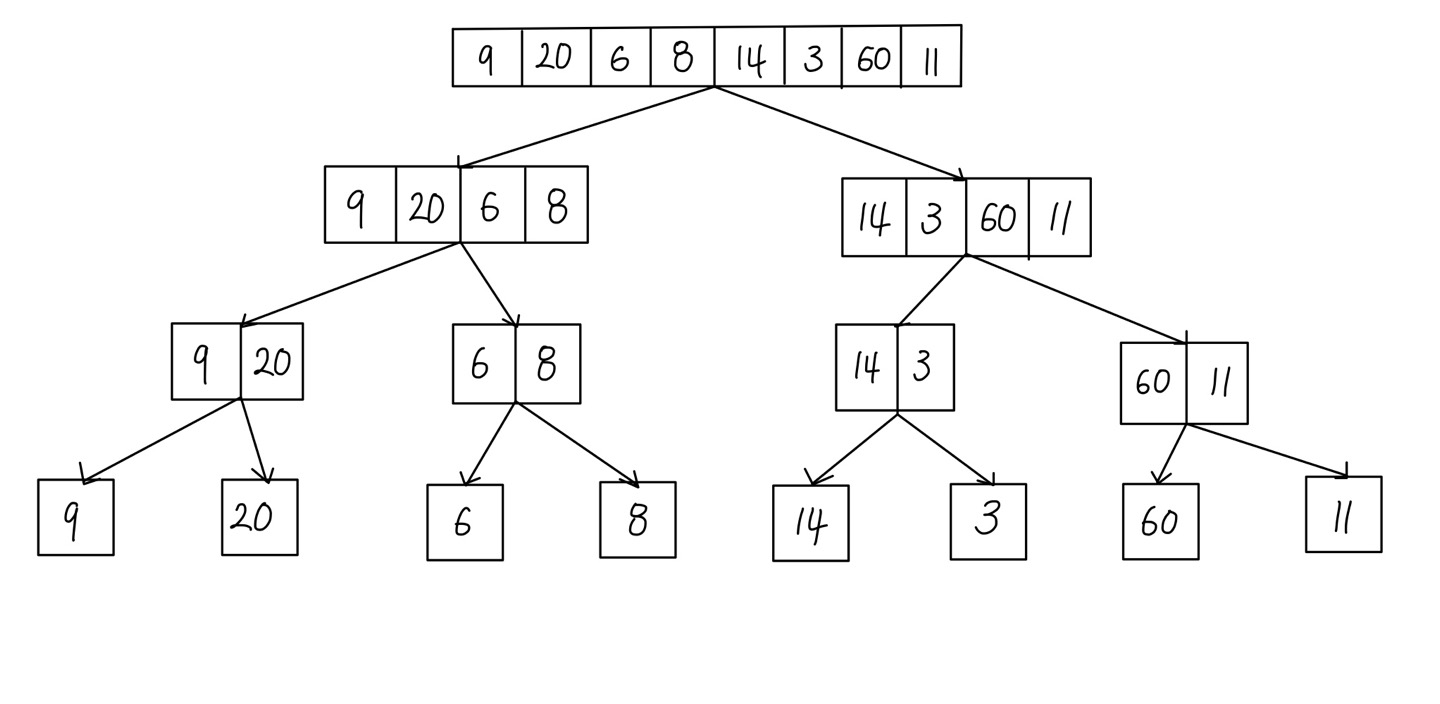

template<class ItemType>
void Merge(ItemType values[], int leftFirst, int leftLast, int rightFirst, int rightLast)
{
ItemType tempArray[SIZE];
int index = leftFirst;
int saveFirst = leftFirst;
while ((leftFirst <= leftLast) && (rightFirst <= rightLast))
{
if (values[leftFirst] < values[rightFirst])
{
tempArray[index] = values[leftFirst];
leftFirst++;
}
else
{
tempArray[index] = values[rightFirst];
rightFirst++;
}
index++;
}
while (leftFirst <= leftLast)
{
tempArray[index] = values[leftFirst];
leftFirst++;
index++;
}
while (rightFirst <= rightLast)
{
tempArray[index] = values[rightFirst];
rightFirst++;
index++;
}
for (index = saveFirst; index <= rightLast; index++)
values[index] = tempArray[index];
}
template<class ItemType>
void MergeSort(ItemType values[], int first, int last)
{
if (first < last)
{
int middle = (first + last) / 2;
MergeSort(values, first, middle);
MergeSort(values, middle + 1, last);
Merge(values, first, middle, middle + 1, last);
}
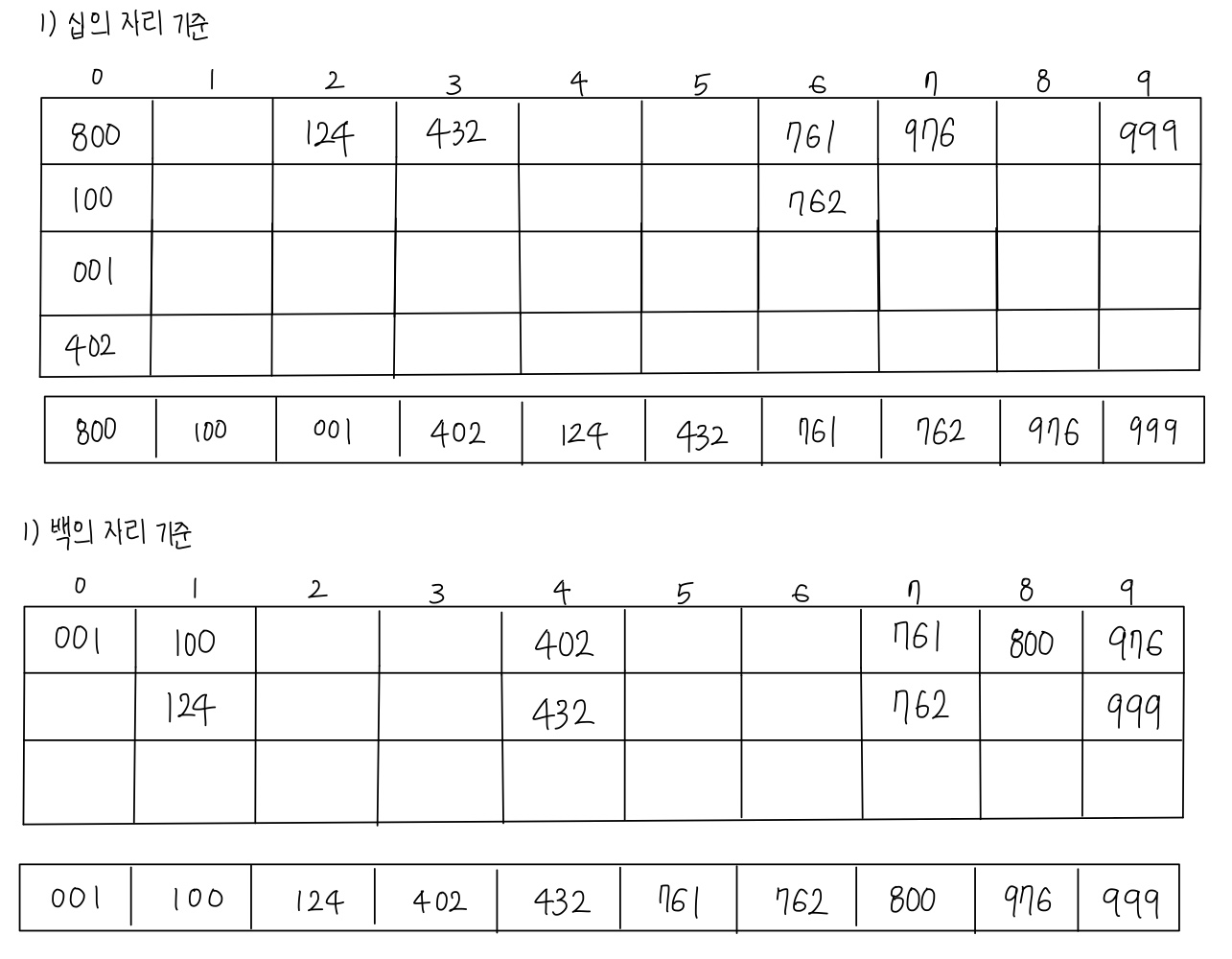
}Radix Sort
- 자릿수가 같은 item들이 저장되어 있을 때
- 뒷자리부터 하나씩 sort
- 0~9 까지 각 자릿수를 위한 Queue가 하나씩 존재
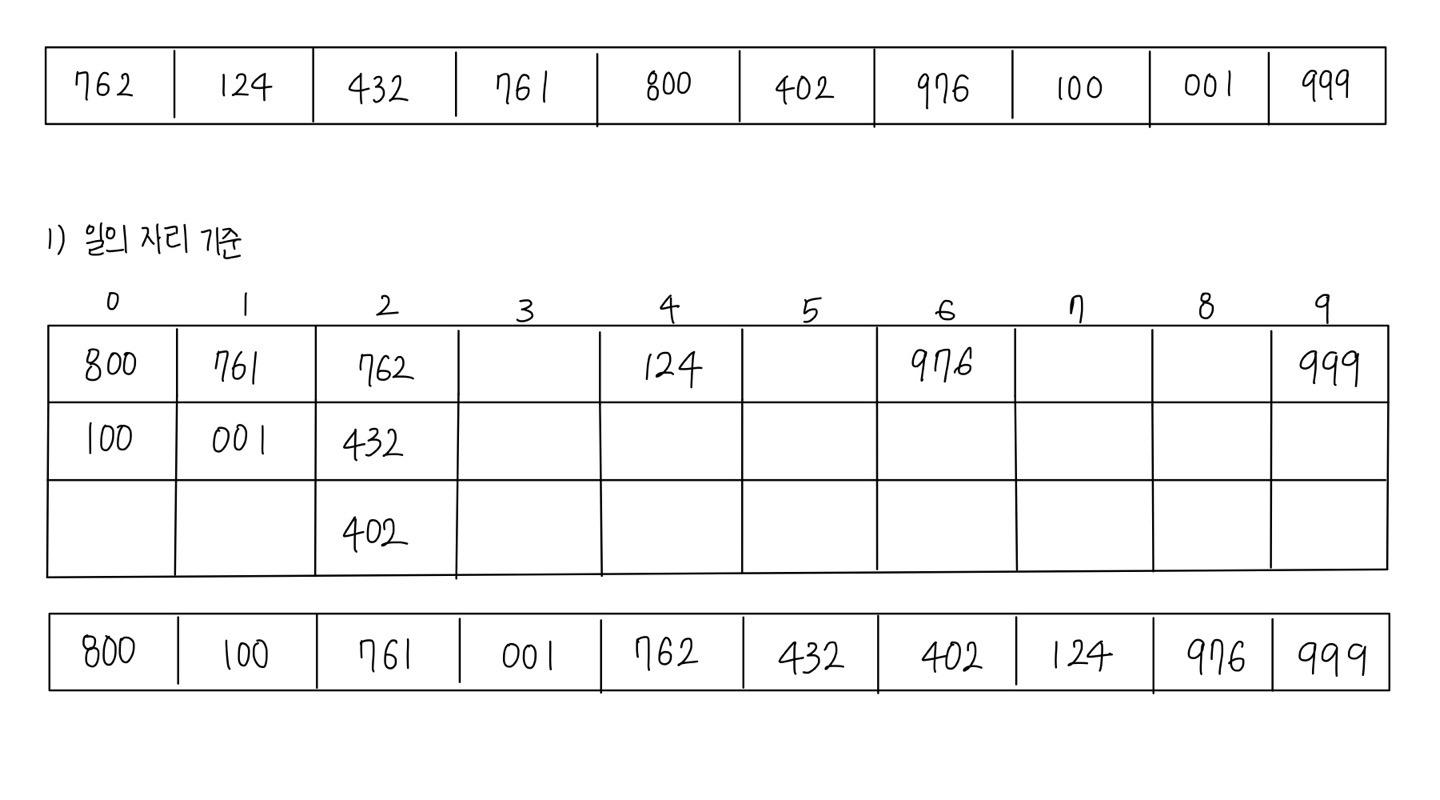
#include "QueType.h"
#include <math.h>
template<class ItemType>
int SubKey(ItemType values, int numPositions, int position)
{
if (values < pow(10, position-1))
return 0;
else
{
int key = (values % static_cast<int>(pow(10, position))) / pow(10, position - 1);
return key;
}
}
template<class ItemType>
void CollectQueues(ItemType values[], QueType<ItemType> queues[], int radix)
{
int index = 0;
ItemType item;
for (int counter = 0; counter < radix; counter++)
{
while (!queues[counter].IsEmpty())
{
queues[counter].Dequeue(item);
values[index] = item;
index++;
}
}
}
template<class ItemType>
void RadixSort(ItemType values[], int numValues, int numPositions, int radix)
{
QueType<int> queues[10];
int whichQueue;
for (int position = 1; position <= numPositions; position++)
{
for (int counter = 0; counter < numValues; counter++)
{
whichQueue = SubKey(values[counter], numPositions, position);
queues[whichQueue].Enqueue(values[counter]);
}
CollectQueues(values, queues, radix);
}
}Big-O Comparison
Big-O Comparison
| Sort | Best Case | Average Case | Worst Case |
|---|---|---|---|
| Selection Sort | O(N^2) | O(N^2) | O(N^2) |
| Bubble Sort | O(N^2) | O(N^2) | O(N^2) |
| Short Bubble Sort | O(N) | O(N^2) | O(N^2) |
| Insertion Sort | O(1) | O(N^2) | O(N^2) |
| Heap Sort | O(N*logN) | O(N*logN) | O(N*logN) |
| Quick Sort | O(N*logN) | O(N*logN) | O(N^2) |
| Merge Sort | O(N*logN) | O(N*logN) | O(N*logN) |
Stability
- 중복된 item이 있을 때, Sorting 후에도 먼저 들어간 item이 앞에 있는 경우
- 중복값들의 순서도 지켜야 할 땐 stable sort 사용
- HeapSort와 QuickSort는 Unstable
Searching
Searching
- Linear Searching
- item을 찾을 확률이 동일할 때 앞에서부터 순차적으로 찾는 방법
- High-Probability Ordering
- item을 찾을 확률이 다를 때 자주 찾는 item은 앞에 배치하는 것
- O(N)
- Key Ordering
- Sorting이 잘 되어 있으면 더 빨리 찾을 수 있음
- Binary Search O(logN)
Hashing
- Hash function을 이용해 한 구조체에 어떤 item이 어느 위치에 저장될지 정해 주는 것
- 데이터들이 고르게 분포하도록 해야 가장 좋은 Hash
- ex 값 1234는 뒤의 두 자리 숫자만 사용하여 34번 index에 저장
- Hash(key) = partNum % 100
- Collision
- 서로 다른 item끼리 같은 위치에 저장되려고 할 때 일어나는 충돌
- 충돌 해결을 위해 Probing 적용
- Linear Probing
- (HashValue + 1) % 100
- (HashValue + constant) % array-size
- Quadratic Probing
+ (HashValue +- i^2) % array-size- 1칸 -> 4칸 -> 9칸 ... 이동
- Random Probing
- (HashValue + random-number) % array-size
Linear Probing
- 충돌을 피하는 방법 중 하나
- 원래의 Hash key에 이미 item이 존재하고 있다면 index를 하나씩 늘려가면서 빈 자리를 찾아서 저장
- Circular 형식으로 마지막 index가 채워져 있을 경우 앞으로 되돌려 다시 탐색
- 쿼리를 이용해 item을 검색할 때도 empty 값까지 찾아봐야 함
- ex) 6702 검색을 위해 2번 index에 접근했더니 3302가 존재할 때
- 3번 index, 4번 index로 넘어가면서 6702 나올 때까지 내려가기
- empty 값이 없는 경우 충돌이 발생했을 때 index를 많이 넘겨야 해서 오래 걸림
- empty가 충분한 table을 만들기 위해 실제 저장되는 item 수보다 여유로운 공간 확보 필요
- Probing이 반복되면 데이터가 뭉쳐진다는 단점 가짐 (데이터끼리 Clustering 생성)
Delete with Linear Probing
| Index | item |
|---|---|
| 0 | empty |
| 1 | 14001 |
| 2 | empty |
| 3 | 50002 |
| 4 | 00104 |
| 5 | 77003 |
| 6 | 42504 |
-
5번 index에 있는 77003을 삭제했을 때
Index item 0 empty 1 14001 2 empty 3 50002 4 00104 5 emty 6 42504 -
42054를 찾기 위해 4번 index 접근
-
Linear Probing으로 5번 index 접근 (Empty)
-
42054는 6번 index에 존재함에도 불구하고 삭제로 인해 없는 아이템이라고 판단
-
item을 삭제할 경우 밑에 있는 item 중에 Linear Probing으로 밀린 item을 다시 위로 올려 주는 작업 필요
Buckets and Chaining
- Bukets
- index 하나에 여러 item들이 저장될 수 있도록 공간 만드는 것
- ex 3개짜리 bucket
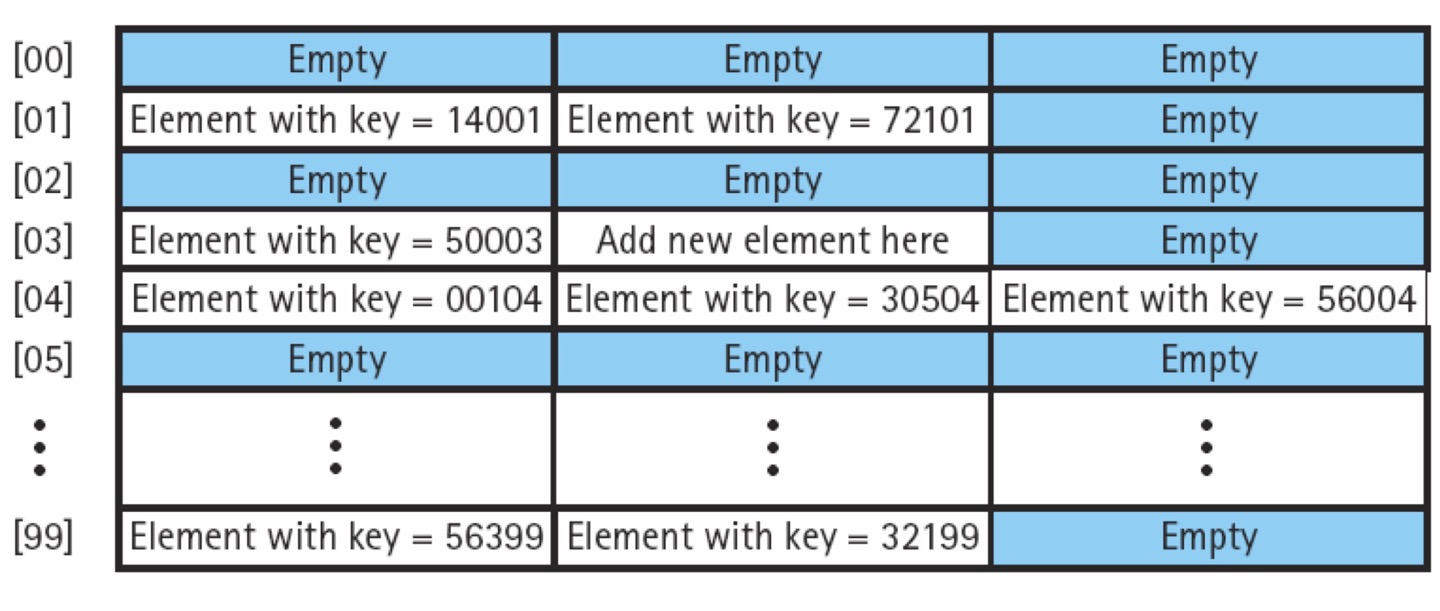
- bucket을 충분하게 설정
- 지나치게 크게 잡을 경우 메모리 낭비
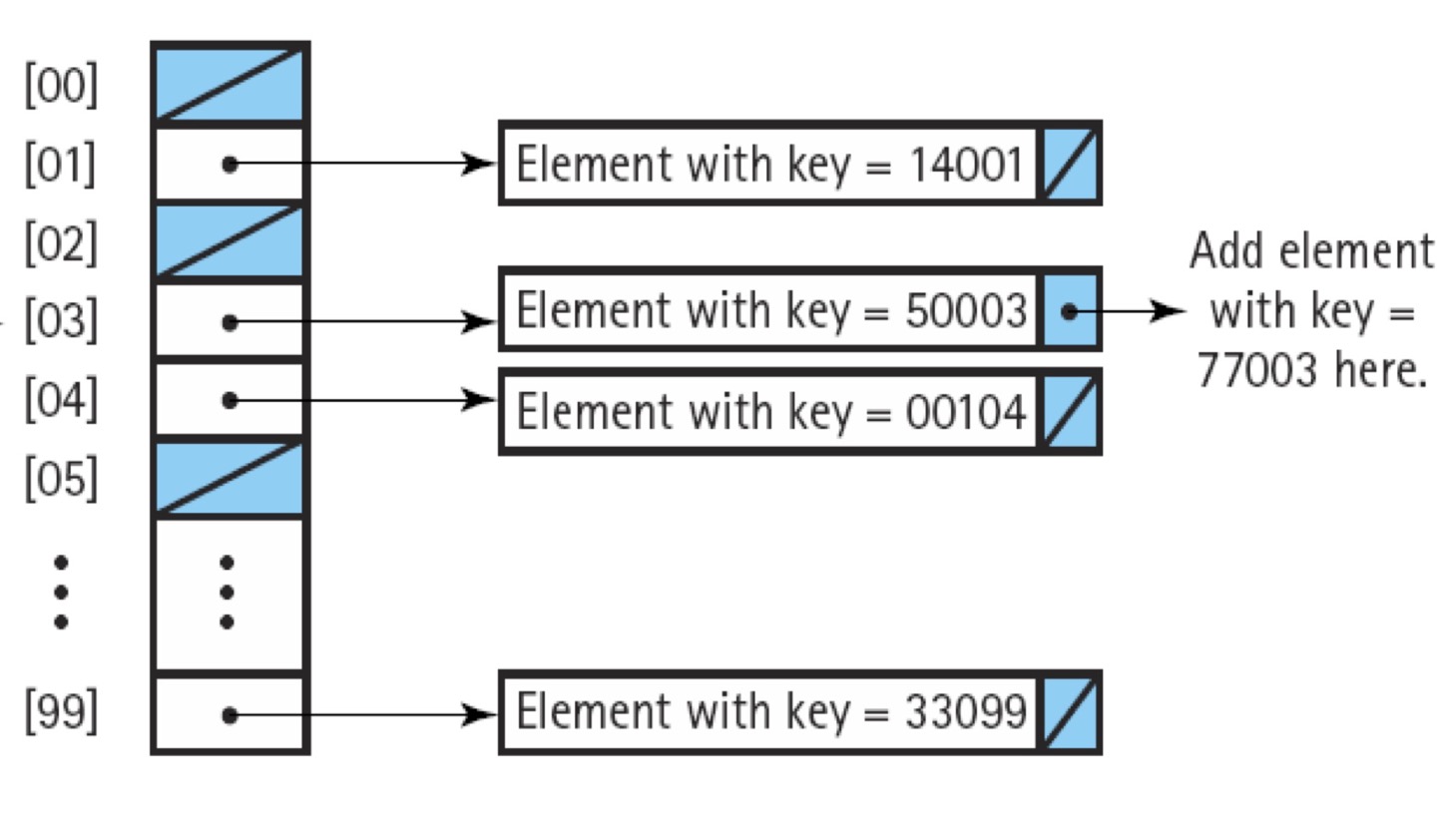
- Chain
- Linked list로 구현
- Probing 불필요
LAP
Student.h
#ifndef _STUDENT_H
#define _STUDENT_H
#include <iostream>
using namespace std;
class Student
{
public:
void Print(ostream& out);
void InitValue(int _id, char* _name, float _gpa);
void getValue(int& _id, char* _name, float& _gpa);
char* getName();
void operator = (Student stu);
private:
int id;
char name[30];
float gpa;
};
void Print(ostream& out, Student stu[], int numelement);
void PrintByPointer(ostream& out, Student* values[], int numValues);
void Print(ostream& out, Student stu[], int numelement)
{
for (int i = 0; i < numelement; i++)
{
stu[i].Print(out);
}
}
void Student::Print(ostream& out)
{
out << id << "\t" << name << "\t" << gpa << endl;
}
void Student::InitValue(int _id, char* _name, float _gpa)
{
id = _id;
strcpy_s(name, sizeof(name), _name);
gpa = _gpa;
}
void Student::getValue(int& _id, char* _name, float& _gpa)
{
_id = id;
strcpy_s(_name, sizeof(name), name);
_gpa = gpa;
}
char* Student::getName()
{
return name;
}
void Student::operator = (Student stu)
{
id = stu.id;
strcpy_s(name, sizeof(name), stu.name);
gpa = stu.gpa;
}
void PrintByPointer(ostream& out, Student* values[], int numValues)
{
for (int i = 0; i < numValues; i++)
{
(*values[i]).Print(out);
}
}
#endifSelection Sort (Name 기준)
#include "Student.h"
#include <string>
int MinIndex(Student values[], int startIndex, int endIndex) {
int IndexOfMin = startIndex;
for (int Index = startIndex + 1; Index <= endIndex; Index++) {
if (strcmp(values[Index].getName(), values[IndexOfMin].getName()) < 0)
IndexOfMin = Index;
}
return IndexOfMin;
}
void SelectionSort(Student values[], int numValues) {
int endIndex = numValues - 1;
for (int current = 0; current < endIndex; current++)
Swap(values[current], values[MinIndex(values, current, endIndex)]);
}Bubble Sort (Name 기준)
#include "Student.h"
void BubbleUp(Student values[], int startIndex, int endIndex) {
for (int index = endIndex; index > startIndex; index--) {
if (strcmp(values[index].getName(), values[index - 1].getName()) < 0)
Swap(values[index], values[index - 1]);
}
}
void BubbleSort(Student values[], int numValues) {
int current = 0;
while (current < numValues - 1) {
BubbleUp(values, current, numValues);
current++;
}
}Insertion Sort (Name 기준)
#include "Student.h"
void InsertItem(Student values[], int startIndex, int endIndex) {
bool finished = false;
int current = endIndex;
bool moreToSearch = (current != startIndex);
while (moreToSearch && !finished) {
if (strcmp(values[current].getName(), values[current - 1].getName()) < 0) {
Swap(values[current], values[current - 1]);
current--;
moreToSearch = (current != startIndex);
}
else
finished = true;
}
}
void InsertionSort(Student values[], int numValues) {
for (int count = 0; count < numValues; count++)
InsertItem(values, 0, count);
}Heap Sort (Name 기준)
template<class ItemType>
void HeapSort(ItemType values[], int numValues) {
int index;
Print(cout, values, 3);
std::cout << std::endl;
for (index = numValues / 2 - 1; index >= 0; index--)
ReheapDown(values, index, numValues - 1);
Print(cout, values, 3);
std::cout << std::endl;
for (index = numValues - 1; index >= 1; index--) {
Swap(values[0], values[index]);
ReheapDown(values, 0, index - 1);
}
}PP
Selection Sort
from typing import MutableMapping
def selection_sort(values):
endIndex = len(values) - 1
for current in range(endIndex):
minIndex = values.index(min(values[current:]))
values[current], values[minIndex] = values[minIndex], values[current]Bubble Sort
def bubble_sort(values):
for i in range(len(values) - 1, 0, -1):
for j in range(i):
if (values[j] > values[j + 1]):
values[j], values[j + 1] = values[j + 1], values[j]Short Bubble Sort
def short_bubble(values, numValues):
current = 0
sorted = False
while(current < numValues - 1 and not sorted):
sorted = bubble_up(values, current, numValues - 1, sorted)
current +=1
def bubble_up(values, startIndex, endIndex, sort):
sorted = True
for index in range(endIndex, startIndex, -1):
if(values[index] < values[index - 1]):
values[index], values[index - 1] = values[index - 1], values[index]
sorted = False
return sorted
Insertion Sort
def insert_item(values, start, end):
finished = False
current = end
moreToSearch = (current != start)
while (moreToSearch and not finished):
if(values[current] < values[current - 1]):
values[current], values[current - 1] = values[current - 1], values[current]
current -= 1
moreToSearch = (current != start)
else:
finished = True
def insertion_sort(values):
for count in range(0, len(values)):
insert_item(values, 0, count)Heap Sort
def reheap_down(elements, root, bottom):
reheaped = False
leftChild = root * 2 + 1
while(leftChild <= bottom and not reheaped):
if(leftChild == bottom):
maxChild = leftChild
else:
rightChild = root * 2 + 2
if (elements[leftChild] <= elements[rightChild]):
maxChild = rightChild
else:
maxChild = leftChild
if(elements[root] < elements[maxChild]):
elements[root], elements[maxChild] = elements[maxChild], elements[root]
root = maxChild
leftChild = root * 2 + 1
else:
reheaped = True
def heap_sort(values, numValues):
for index in range(int(len(values)/2 - 1), 0, -1):
reheap_down(values, index, len(values)-1)
for index in range(int(len(values)-1), 0, -1):
values[0], values[index] = values[index], values[0]
reheap_down(values, 0, index - 1)Quick Sort
def split(values, first, last):
splitvalue = values[first]
saveFirst = first
onCorrectside = True
first += 1
while(first <= last):
while(onCorrectside):
if(values[first]>splitvalue):
onCorrectside = False
else:
first += 1
onCorrectside = (first <= last)
onCorrectside = (first <= last)
while(onCorrectside):
if(values[last] < splitvalue):
onCorrectside = False
else:
last -= 1
onCorrectside = (first <= last)
if(first <= last):
values[first], values[last] = values[last], values[first]
first += 1
last -= 1
splitPoint = last
values[saveFirst], values[splitPoint] = values[splitPoint], values[saveFirst]
return splitPoint
def quick_sort(values, first, last):
if(first < last):
splitPoint = split(values, first, last)
quick_sort(values, first,splitPoint-1 )
quick_sort(values, splitPoint+1, last)
return valuesMerge Sort
def merge_sort(values, first, last):
if(first < last):
middle = int((first + last) / 2)
merge_sort(values, first, middle)
merge_sort(values, middle + 1, last)
merge(values, first, middle, middle + 1, last)
def merge(values, leftFirst, leftLast, rightFirst, rightLast):
tempArray = []
saveFirst = leftFirst
while ((leftFirst <= leftLast) and (rightFirst <= rightLast)):
if (values[leftFirst] < values[rightFirst]):
tempArray.append(values[leftFirst])
leftFirst += 1
else:
tempArray.append(values[rightFirst])
rightFirst += 1
while(leftFirst <= leftLast):
tempArray.append(values[leftFirst])
leftFirst += 1
while(rightFirst <= rightLast):
tempArray.append(values[rightFirst])
rightFirst += 1
for index in range(saveFirst, rightLast):
values[index] = tempArray[index-saveFirst]
