CH 03 ADTs Unsorted List and Sorted List

List

List

• List: Data Element 사이에 Linear Relationship을 가지는 경우
• Linear Relationship
  • 첫 번째 요소를 제외한 각 요소에는 고유한 선행 요소 존재
  • 마지막 요소를 제외한 각 요소에는 고유한 후속 요소 존재
• Length: List 안에 있는 Data Item의 수
• Unsorted List
  • 데이터 항목이 특별한 순서로 배치되지 않은 List
  • 데이터 요소 간의 유일한 관계는 선행 및 후속
• Sorted List
  • 키의 값에 따라 정렬되는 List
  • List와 키 사이에 의미적 관계 존재
• Key: List를 Sort하기 위한 Attribute
• ADT: 값의 범위와 Operation 정보만 제공하고 직접적인 구현은 숨기는 Data Type

Class Constructor

• Return 값이 없고 Class와 이름이 같음
• 생성자 Overloading 가능
• Default Constructor
  • Implicity invoked: 부르지 않아도 자동으로 구현
  • 직접 구현한 생성자가 있을 경우, Default Constructor가 자동으로 생성되지 않기 때문에 직접 작성해야 함
  • 모든 Class는 반드시 한 개 이상의 생성자 필요

Generic Data Type

• Operation은 정의되었지만 Data Type은 정의되지 않았을 때
• Data Type과 무관하게 Operation이 잘 작동하도록 하기 위함
• ComparedTo Method: Data Type을 알아야 비교 가능하기 때문에 Generic Data Type 밑에 구현

Unsorted List

ADTs Unsorted List Operation

• Transformer
  • MakeEmpty
  • InsertItem
  • DeleteItem
• Observe
  +
  • IsFull
  • LengthIs
  • RetriveItem
• Iterators
  • ResetList
  • GetNextItem

ItemType.h

const int MAX_ITEMS = 100;
enum RelationType {LESS, EQUAL, GREATER};

class ItemType {
public: 
    RelationType CompareTo(ItemType other) const;
    void print() const;
    void Initialize(int number);
private:
    int value;
};

ItemType.cpp

#include "ItemType.h"
#include <iostream>

RelationType ItemType::CompareTo(ItemType other) const {
	if (value < other.value)
		return LESS;
	else if (value == other.value) 
		return EQUAL;
	else
		return GREATER;
}

void ItemType::print() const {
	std::cout << value << std::endl;
}

void ItemType::Initialize(int number) {
	value = number;
}

Unsorted.h

#include "ItemType.h"
#define MAX_ITEMS 100

class UnsortedType {
public:
	UnsortedType();
	void MakeEmpty();
	void InsertItem(ItemType item);
	void DeleteItem(ItemType item);
	bool IsFull();
	int LengthIs();
	void RetrieveItem(ItemType& item, bool& found);
	void ResetList();
	void GetNextItem(ItemType &item);
private:
	int length;
	ItemType info[MAX_ITEMS];
	int currentPos;
};

Unsorted.cpp

#include "unsorted.h"

UnsortedType::UnsortedType() {
	length = 0;
} 

void UnsortedType::MakeEmpty() {
	length = 0;
}

void UnsortedType::InsertItem(ItemType item) {
	info[length] = item;
	length++;
}

void UnsortedType::DeleteItem(ItemType item) {
	int location = 0;
	while (item.ComparedTo(info[location]) != EQUAL) //item과 info[location]이 다르다면
		location++; //location 업데이트
	info[location] = info[length - 1]; //뒤에 있는 애 아무나 끌어다 쓰기
	length--;
}

bool UnsortedType::IsFull() {
	return (length == MAX_ITEMS);
}

int UnsortedType::LengthIs() {
	return length;
}

void UnsortedType::RetrieveItem(ItemType& item, bool& found) {
	found = false;
	int location = 0;
	bool moreToSearch = (location < length);
	while (moreToSearch && !found) {
		switch (item.ComparedTo(info[location])) {
		case LESS:
		case GREATER:
			location++;
			moreToSearch = (location < length);
		case EQUAL:
			found = true;
			item = info[location];
        }
	}
}

void UnsortedType::ResetList() {
	currentPos = 0;
}

void UnsortedType::GetNextItem(ItemType &item) {
	item = info[currentPos];
	currentPos++;
}

Sorted List

InsertItem Method

• 새 요소를 넣어야 할 위치 찾기
• 새 요소 뒷 순서를 하나씩 뒷 index로 밀어서 자리 생성
• 빈 공간에 요소 삽입
• 길이 증가

DeleteItem Method

• 지워야 할 요소가 있는 위치 찾기
• 지워야 할 요소의 뒷 요소부터 하나씩 앞당기기
• 길이 감소

RetrieceItem Methos

• n개의 Item이 있을 때 n번 다 비교하는 것은 비효율적인 방법
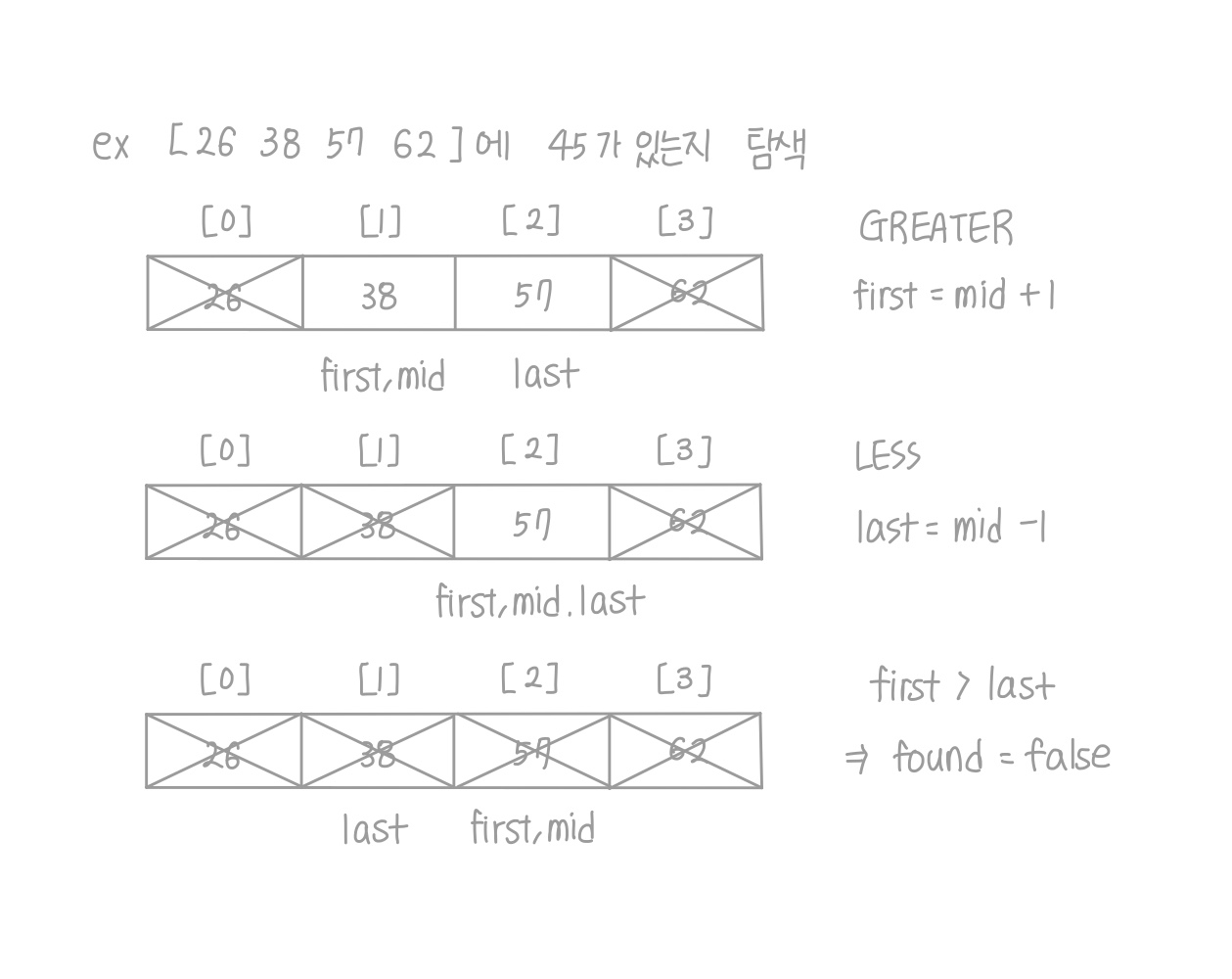
• Binary Search: 배열의 중간 위치 원소와 비교해 앞인지 뒤인지 판단
• bool moreToSearch = (first < last) 필수
  • 만약 다 검색해도 찾고자 하는 아이템이 없다면 first = last
  • moreToSearch로 제약을 걸지 않으면 무한 루프에 빠짐
    

Sorted.h

#include "ItemType.h"
#define MAX_ITEMS 100

class SortedType {
public:
	SortedType();
	void MakeEmpth();
	void InsertItem(ItemType item);
	void DeleteItem(ItemType item);
	bool IsFull();
	int LengthIs();
	void RetrieveItem(ItemType& item, bool& found);
	void ResetList();
	void GetNextItem(ItemType& item);
private:
	int length;
	ItemType info[MAX_ITEMS];
	int currentPos;
};

Sorted.cpp

#include "Sorted.h"

SortedType::SortedType() {
	length = 0;
}

void SortedType::MakeEmpth() {
	length = 0;
}

void SortedType::InsertItem(ItemType item) {
	int location = 0;
	bool moreToSearch = (location < length);
	while (moreToSearch) {
		switch (item.ComparedTo(info[location])) {
			case LESS:
				moreToSearch = false;
			case EQUAL:
				location++;
				moreToSearch = (location < length);
            }
	}
	for (int index = length; index > location; index--) {
		info[index] = info[index - 1];
	}
	info[location] = item;
	length++;
}

void SortedType::DeleteItem(ItemType item) {
	int location = 0;
	while (item.ComparedTo(info[location]) != EQUAL)
		location++;
	for (int index = location + 1; index < length; index++) {
		info[index - 1] = info[index];
		length--;
	}
}

bool SortedType::IsFull() {
	return(length == MAX_ITEMS);
}

int SortedType::LengthIs() {
	return length;
}

void SortedType::RetrieveItem(ItemType& item, bool& found) {
	int first = 0;
	int last = length - 1;
	int mid;
	bool moreToSearch = (first < last);
	found = false;
	while (moreToSearch && !found) {
		mid = (first + last) / 2;
		switch (item.ComparedTo(info[mid])) {
			case LESS:
				last = mid - 1;
				moreToSearch = (first < last);
			case EQUAL:
				found = true;
			case GREATER:
				first = mid + 1;
				moreToSearch = (first < last);
            }
	}
}

void SortedType::ResetList() {
	currentPos = 0;
}

void SortedType::GetNextItem(ItemType& item) {
	item = info[currentPos];
	currentPos++;
}

Algorithm & Complexity

Comparision Algorithm

• Executive Tiem: 컴퓨터 기기에 따라 변동적
• Number of Statement: 절대적인 기준으로 삼을 수 없음
• Number of Fundamental Operation

Big-O Notation, Complexity

• 데이터가 n개 있을 때 Operation이 수행되는 차수

• 최악의 경우로 따짐

  • ex) 가장 마지막에 있는 Item을 Retrieve 하는 경우

• 가장 빠르게 증가하는 Size로 표현

  • f(N) = N^4 + 100N^2 일 때 시간복잡도는 O(N^4)
  • n이 무한으로 커지면 상수가 무의미해지기 때문
  • 증가율이 가장 높은 항으로 결정

• Names of Orders of Magnitude

  • O(1): Bounded Time
  • O(log_2⁡(N)): Logarithmic Time (Binary Search)
  • O(N): Linear Time (Seqential Search)
  • O(N^2): Quadratic Time
  • O(e^N): Exponential Time

• Big-O Comparison of List Operation

  Operation	UnsortedType	SortedType
  Constructor	O(1)	O(1)
  MakeEmpty	O(1)	O(1)
  InsertItem	O(1)	O(N)
  DeleteItem	O(N)	O(N)
  IsFull	O(1)	O(1)
  LengthIs	O(1)	O(1)
  RetrieveItem	O(N)	O(log_2⁡(N))
  ResetList	O(1)	O(1)
  GetNextItem	O(1)	O(1)