Abstract

경사 하강 최적화 알고리즘은 대중적으로 사용되고 있지만 장점과 단점에 충분한 설명을 하기 어려워서 블랙박스 최적화 도구로 사용된다.

이 논문에서는 일반적인 최적화 알고리즘을 설명하고, 병렬 및 분산환경에서 아키텍처를 검토하고, 경사하강법의 다양한 전략을 소개한다.

1 Introduction

경사하강법은 최적화를 수행하는 가장 일반적인 알고리즘이고 신경망을 최적화하는 가장 일반적인 방법이다. 다양한 라이브러리에서 수행되는 경사하강법 알고리즘은 블랙박스 옵티마이저를 사용해서 장점과 단점에 대한 실용적인 설명이 어렵다. 논문에서는 다양한 경우 경사하강법을 사용할 때 선택하는 가이드를 제공한다. 경사하강법은 목적함수 J(세타)를 최적화하는것으로 목적함수의 도함수 기울기와 반대로 세타를 움직인다. learning rate η는 minimum에 도달하기 위한 step size이다.

즉, 최소치에 도달하기위해 경사의 방향을 내려막길로 따라간다

learning rate는 경사하강을 할 때 얼마나 이동하는지에 대한 값이다.

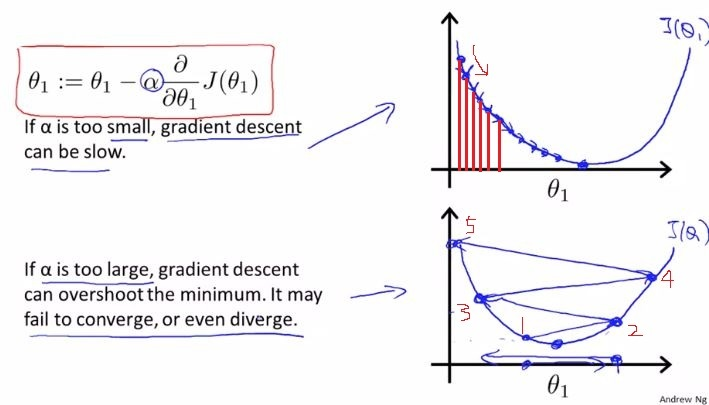
2 Gradient decent variants(경사 하강 변형)

경사하강법의 변형에는 세 가지 변형이 있다. 목적함수J()를 계산하기 위한 데이터 양에 따라 그 방법이 달라진다.

데이터의 양에 따라 변수(세타)를 업데이트하는 과정과 업데이트수행하는데 걸리는 시간을 절충한다

2.1 Batch gradient descent

전체 데이터 세트에 대해서 세타에 대해 그레디언트를 계산한다

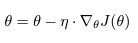
업데이트를 한 번 할 때마다 전체 데이터 세트에 대한 그레이디언트를 계산하므로 속도가 느릴 수 있다.

온라인으로 모델을 사용할 수 없다.(새로운 데이터가 계속 추가되는 경우)

2.2 Stochastic gradient descent

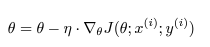
SGD는 배치 경사 하강법과는 다르게 한 번에 하나의 업데이트만 진행한다. 그래서 훨씬 빠르고 온라인에서 사용가능

전체 데이터에 대해서 무작위 샘플에 대해서만 경사를 측

SGD는 빈번한 업데이트가 있고 변동이 심하다

배치 경사하강법과 다르게 지역 최적해를 건너뛰어 전역 최적해에 다다를 수 있다

learning rate를 서서히 줄이면 배치 경사 하강법처럼 동작을 한다고 한다

2.3 Mini-batch gradient descent

위의 두 장점을 합쳤다

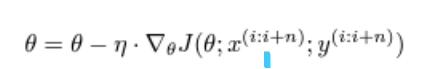
n개의 데이터를 미니배치로 처리한다.(일반적으로 미니배치 사이즈는 50~256)

세타의 업데이트 다양성을 감소시켜 안정적인 수렴으로 이어질 수 있다

미니배치 경사하강법은 일반적으로 신경망을 훈련시길때 선택되고 SGD라는 용어는 미니배치를 사용할때도 사용한다고한다.

3 Challenges

위의 경사하강법들은 몇 가지 어려움이 있을 수 있다

1. 적절한 학습률을 선택하기 어렵다
2. 학습률을 조정하기 힘들다
3. 모든 데이터에 같은 학습률을 적용하는데 우리는 그렇게 하고 싶지 않을 수 있다

4 Gradient descent optimization algorithms

4.1 Momentum

SGD는 최저점을 찾으러갈 때 경사면을 가로질러 진동을 많이 하는 단점이 있다 따라서 모멘텀(관성)을 이용해 더 빠르게 최적해를 찾아나간다

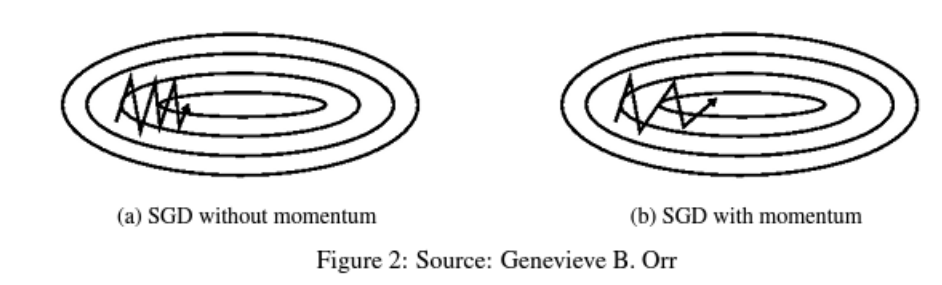
모멘텀은 SGD를 다른방향으로 가속화하고 진동을 완화하는데 도움을 주고 과거의 속도를 활용해 파라미터를 업데이트한다

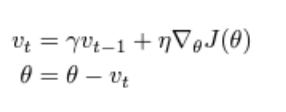
γ는 일반적으로 0.9로 둔다

공을 경사면에서 굴릴 때 점점 빨라지는것 처럼 vt가 증가하여 gradient가 가르키는 방향보다 관성이 가르키는 방향이 더 커지게된다

4.2 Nesterov accelerated gradient(NAG)

모멘텀은 최솟값에 다다랐을 때 관성때문에 왔다갔다 할 수 있다

그래서 이동 전에 모멘텀에의한 위치를 확인하고 그레이디언트 방향으로 움직이는 아이디어이다.

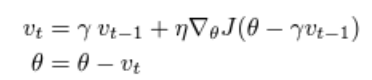
J(θ−γvt−1) 부분을 보면 원래의 위치에서 모멘텀을 계산한 후에 그레이디언트를 계산하는 것이다.

일반적인 모멘텀의 경우 파란색 화살표 처럼 현재 그레이디언트 계산후 누적된 값을 계산해서 나아간다 그러나 Nesterov 는 갈색벡터 방향으로 이전에 누적된 빙향으로 이동하고 그 위치에서 그레이디언트를 계산해 그 방향(빨간벡터)를 보정해서 이동한다

4.3 Adagrad

아다그라드는 학습률을 파라미터(세타)에 맞게 조정하는 아이디어

이전의 파라미터에 대한 그레이디언트를 계산해서 그 값이 큰 것은 학습률을 줄이고 그 값이 작은것은 학습률을 높인다

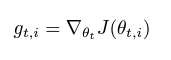
시간마다 각 파라미터의 그레이디언트를 계산한다

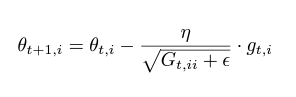
과거에 계산된 그레이디언트를 기반으로 파라미터를 업데이트 한다.

Gt,ii는 누적된 기울기의 제곱값을 행렬로 표현한 것이고 입실론은 분모가 0이 되지 않게하는 파라미터

Adagrad는 분모에 기울기가 계속 누적되므로 학습률이 줄어들고 결국 무한히 작아지는 단점이 있다. 그래서 Adagrad는 더 이상 추가의 정보를 학습 하지 못할 수 있다.

루트를 씌운것이 학습속도에 긍정적인 영향을 준다고 한

4.5 RMSprop

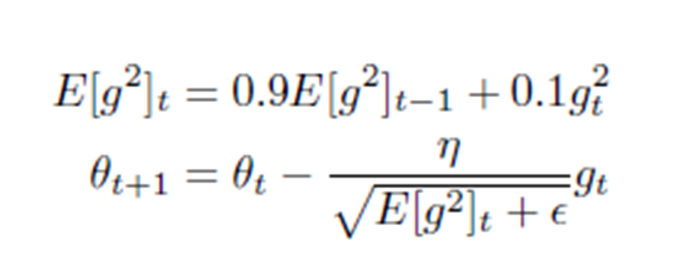
4.6 Adam

4.9 Visualization of algorithms

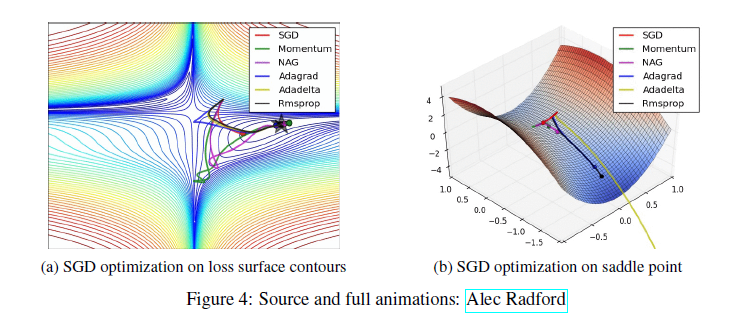
왼쪽그림에서 모멘텀과 NAG는 궤도를 벗어나 언덕 아래로 굴러가는 공의 이미지를 연상시킨다

오른쪽 그림 안장지점(saddle points)에서는 SGD, 모멘텀, NAG는 대칭을 깨기 어렵다는 것을 알 수 있다

4.10 Which optimizer to use?

데이터가 sparse한 경우 adaptive learning rate method를 사용하는것이 효과

일반적으로 adam optimizer가 좋은 성능이고 흥미롭게도 많은 논문에서는 vanilla SGD를 사용한다고 한다

6 Additional strategies for optimizing SGD

6.1 Shuffling and Curriculum Learning

일반적으로 모델에 의미있은 순서로 훈련 데이터를 제공하지 않는것이 좋다

최적화 알고리즘에 편향성을 줄 수 있기때문

따라서 매 epoch마다 데이터를 shuffle하는것이 좋다

6.2 Batch normalization

학습을 용이하게 하기 위해 parameter의 초기 값을 정규화한다

학습이 진행되고 심화됨에 따라 학습 속도가 느려지고 변동 사항이 증폭된다

이를 해결하기 위해 모든 미니 배치에 대해 정규화를 다시 설정한다

6.3 Early stopping

훈련 중 오류가 충분히 개선되지 않을 경우 중단

제프리 힌튼: early stopping은 공짜 점심과 같다

6.4 Gradient noise

가우시안 노이즈를 가중치에 추가하면 깊고 복잡한 네트워크를 훈련하는데 도움을 준다

노이즈로 인해 최적해를 찾는 기회가 더 많아진다고 한다