1.BFS를 알기 전에 필요한 개념
📖 그래프란?
여러 개의 노드(node)와 이들을 연결하는 간선(Edge)으로 이루어진 자료구조이다.
📖 queue란?
한쪽 끝에서만 삽입이 이루어지고, 다른 한쪽 끝에서는 삭제 연산만 이루어 지는 유한 순서 리스트.
선입 선출, First in First Out(FIFO) 먼저 들어온 것이 먼저 나감!
2.BFS (너비 우선 탐색, Breadth first Search)
시작점에서 가까운 정점부터 순서대로 방문하는 탐색 알고리즘
BFS 탐색 방법
-
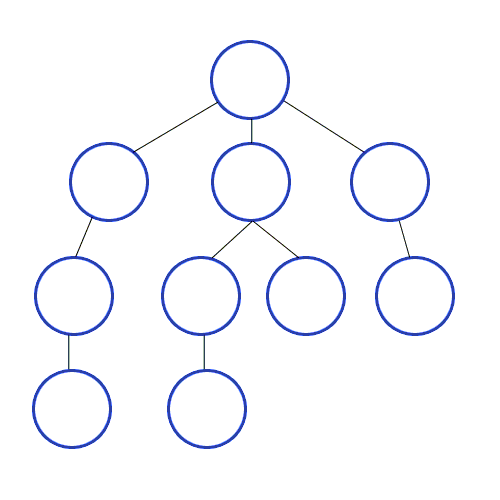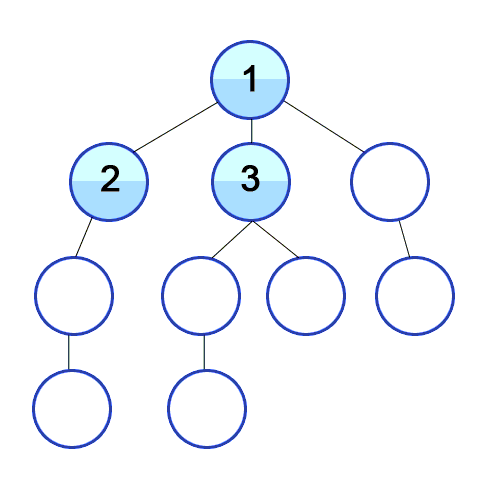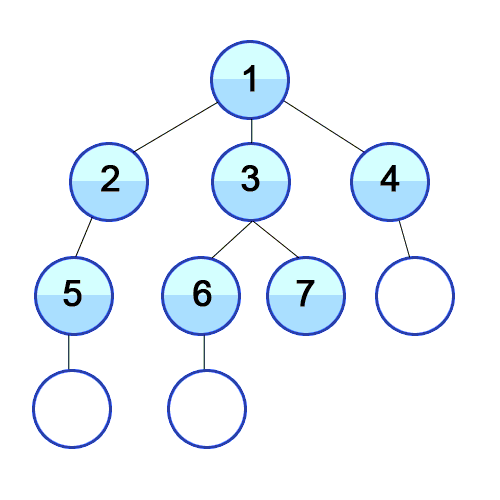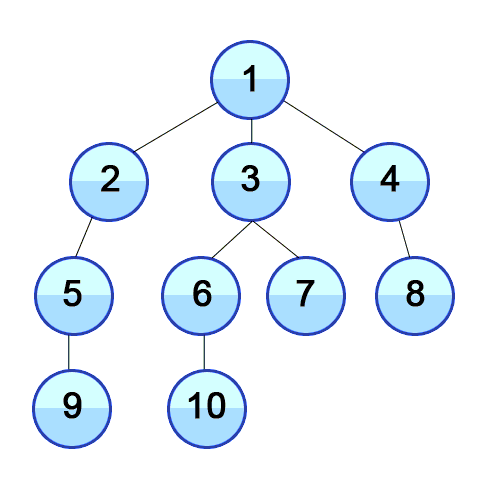
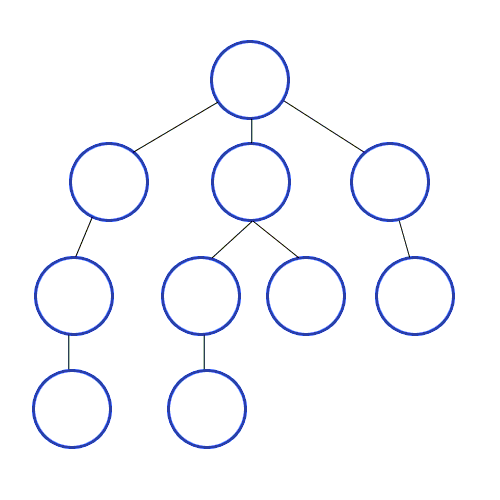
BFS는 시작점에서 가까운 정점부터 탐색하기 위해 방문이 필요한 노드를 큐에 담아놓고 하나씩 방문한다.
→ 1번을 시작으로 큐에 2,3,4번 노드를 담아놓는다.
( visited = [1] , queue = [2,3,4])
→ 큐에 가장 먼저 들어간 2번을 꺼내서 방문하고 2번 노드와 인접한 5번을 큐에 담는다.
( visited = [1,2], queue = [3,4,5])
→ 위와 같은 방법으로 먼저 들어간 노드 방문한 다음 해당 노드와 인접한 노드 큐에 담기 반복
( visited = [1,2,3], queue = [ 4,5,6,7])
→ ( visited = [1,2,3,4] , queue = [5,6,7,8])
→ ( visited = [1,2,3,4,5] , queue = [6,7,8,9])
→ (visited = [1,2,3,4,5,6] , queue = [7,8,9,10])
→ 7,8,9,10번은 방문하지 않은 노드 중 인접한 노드가 없으므로
→ (visited = [1,2,3,4,5,6,7] , queue = [8,9,10])
→ (visited = [1,2,3,4,5,6,7,8] , queue = [9,10])
→ (visited = [1,2,3,4,5,6,7,8,9] , queue = [10])
→ (visited = [1,2,3,4,5,6,7,8,9,10] , queue = []) -
stack과 재귀 방식 둘 다 사용 가능한 DFS 와 달리 BFS는 큐를 사용해서 구현한다.
BFS 알고리즘을 주로 사용하는 문제
최단거리 구하기 , 단계별 탐색 , 완전 탐색 (DFS보다 빠름) 등의 문제에서 사용할 수 있다.
BFS 코드 구현 (JS 버전)
- 1편인 dfs 와 같은 인접 리스트? 형태의 graph 라고 생각해보자!
const graph = [[],[2,5,9],[1,3],[2,4],[3],[1,6,8],[5,7],[6],[5],[1,10],[9]]
// 리스트 자리수 : 연결된 노드
// 1번 노드 : [2,5,9] 번 노드와 연결
bfs 코드 작성해보면
function bfs(graph,startNode){
const visited = []; // 방문한 노드들
let needVisit = []; // 방문이 필요한 노드들
needVisit.push(startNode); // 처음 방문을 시작할 노드
while (needVisit !== 0){ // 1. 방문할 노드가 존재 한다면
const node = needVisit.shift(); // 1. 선입선출(FIFO) 구조라 shift 함수 사용
if(!visited.includes(node){
visited.push(node)
const nodes = graph[node].slice().sort((a,b) => a - b); // 복사 후 오름차순 정렬
needVisit = [...needVisit, ...nodes] ; // queue 형태를 사용하니까 나중에 방문할 데이터 쌓아 놓기
}
}
return visited
}
bfs(graph,1)이런 구조로 흘러가게 된다
근데 사실 위에 풀이는 백준의 1260.DFS와 BFS 문제를 풀때 사용했던 방식이라 문제에 따라 맞게 쓰는 풀이들도 적어 볼려고 한다!
BFS 최단거리 문제 (JS 버전)
백준의 2178.미로탐색 문제를 예시로 들어보겠다.
해당 문제는 시작점에서 도착 위치까지의 최단 거리를 구하는 문제이고, 1로 된 곳으로만 이동이 가능하다.
const graph = [
[ 1, 0, 1, 1, 1, 1 ],
[ 1, 0, 1, 0, 1, 0 ],
[ 1, 0, 1, 0, 1, 1 ],
[ 1, 1, 1, 0, 1, 1 ]
]
const M = 6; // x 최대 길이
const N = 4; // y 최대 길이 dx = [0,0,-1,1]; // 상하좌우
dy = [-1,1,0,0]; // 상하좌우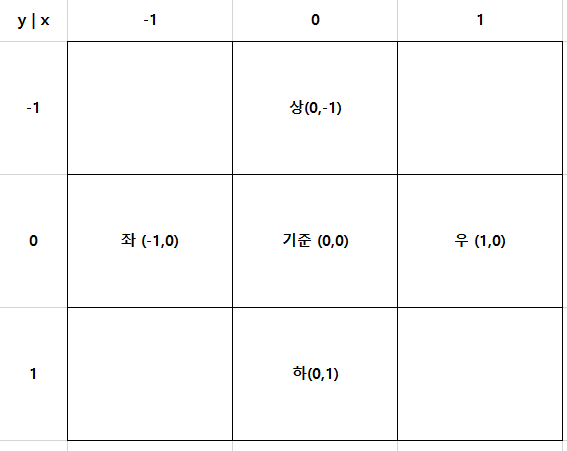
해당 표를 보면 기준 좌표(0,0)에 따라 이동할 값을 리스트 형태로 작성하였다.
function bfs(start_x,start_y,cnt){
const queue = [];
queue.push([start_x,start_y,cnt]); // 시작하는 x,y,cnt 값 큐에 담기
while(queue.length!==0){ // 방문해야 할 위치가 큐에 담긴 경우
const [x,y,cnt] = queue.shift(); // 가장 먼저 담겨있던 노드 꺼냄
for(let i = 0; i<4; i++){ // 상하좌우 탐색을 위한 for 문
const nx = x+dx[i]
const ny = y+dy[i]
if(nx>=0 && nx < N && ny >= 0 && ny < M){ // graph 범위안에 들어오고
if(graph[nx][ny] == 1){ // 이동 가능한 구간인 경우
graph[nx][ny] = cnt+1 // 해당 칸에 누적 이동거리 + 1 을 해준다.
queue.push([nx,ny,cnt+1]) // 해당 위치에서 이동 가능한 곳이 있는지 확인하기 위해 queue에 담아준다.
}
}
}
}
return graph[N-1][M-1] // 도착위치에 최단거리를 확인 할 수 있다.
}
bfs(0,0,1)✍️ 후기
-
dfs 작성하고 bfs 문제도 어느정도 다 푼 상태에서 글을 작성하니까 이전 보다 좀 더 빨리 작성한 느낌이 들었다.
-
미래의 내가 안까먹었으면 좋겠지만.. 까먹었을 때 잘 참고해서 빨리 기억하길 바란다...
-
이전에는 개념을 덜 숙지한 상태에서 문제를 많이 풀어서 코테를 준비한것 같은데, 이번엔 개념 -> 문제 순서의 정석으로 하니까 오히려 빠른거 같다는 생각이 들었다. 꾸준히 해야지!
출처: