이해한 대로 적어보는 알고리즘(JS) - 1. DFS

밍구·2025년 4월 25일

DFS depth first search stack 그래프 깊이 우선 탐색 스택 알고리즘 재귀함수

이해한대로 적어보는 알고리즘

목록 보기

2/3

1.DFS를 알기 전에 필요한 개념

📖 그래프란?

여러 개의 노드(node)와 이들을 연결하는 간선(Edge)으로 이루어진 자료구조이다.

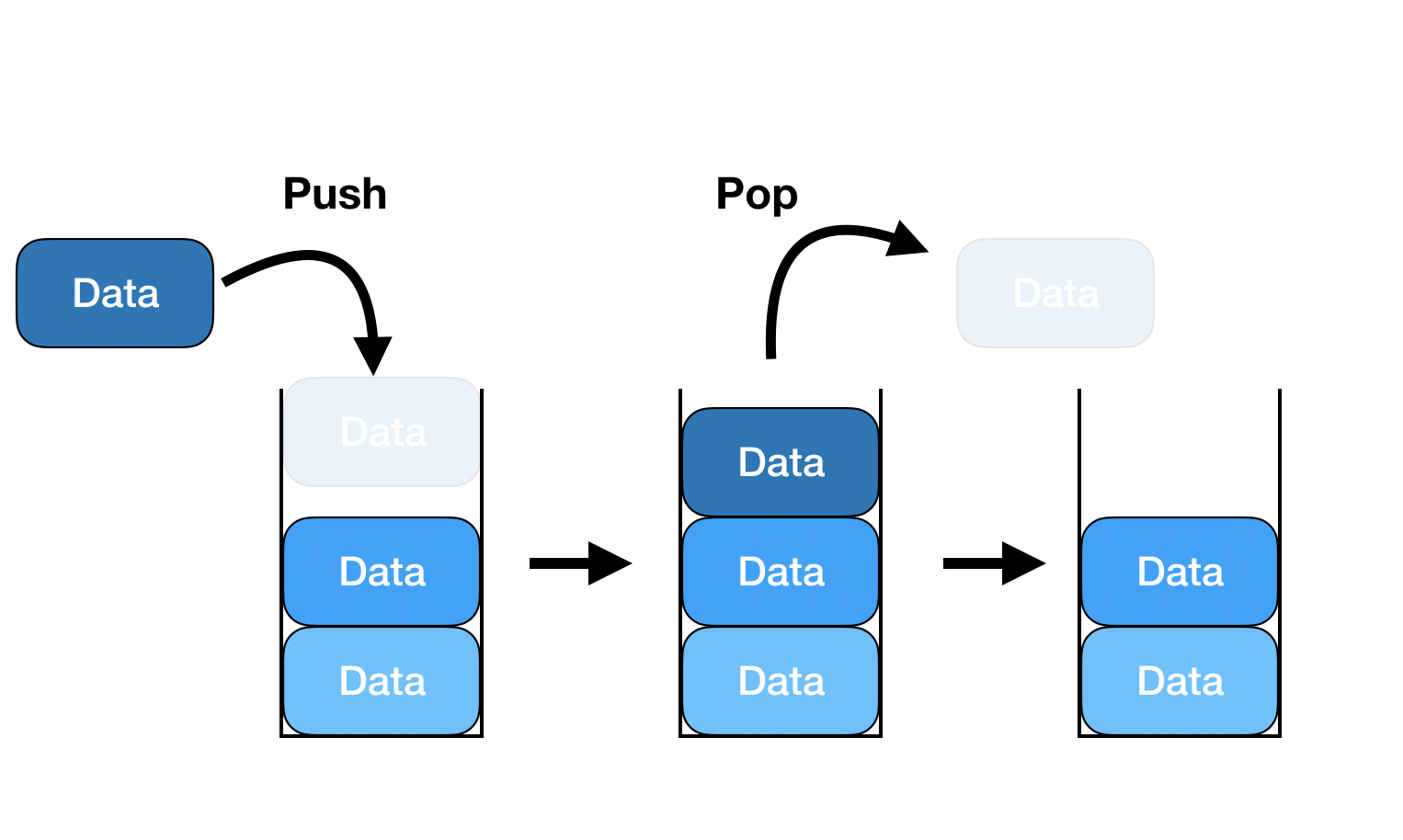
📖 stack이란?

한쪽 끝에서 자료를 넣거나 뺄 수 있는, 데이터를 제한적으로 접근할 수 있는 구조 ,
(LIFO)후입-선출 구조 : 뜻이 후입 (list끝) 선출(list 앞)아니라 list 끝에 넣고 최근에 넣은걸 뺀다는 뜻!

📖 재귀 함수

함수 안에 자신의 함수를 다시 호출하는 함수를 의미한다.
이러한 재귀함수는 자신의 로직을 내부적으로 반복하다가, 일정한 조건이 만족되면 함수를 이탈하여 결과를 도출한다.

2.DFS (깊이 우선 탐색, Depth-First Search)란?

DFS 탐색 방법

DFS는 하나의 방향을 결정하면 그 방향을 따라 끝까지 도달한다.
해당 그림을 예시로 들면,
→ 1번을 시작으로 인접한 2,5,9번 노드 중 왼쪽 노드 부터 탐색한다.
→ 2번 노드와 인접한 3번 탐색
→ 3번과 인접한 4번 탐색
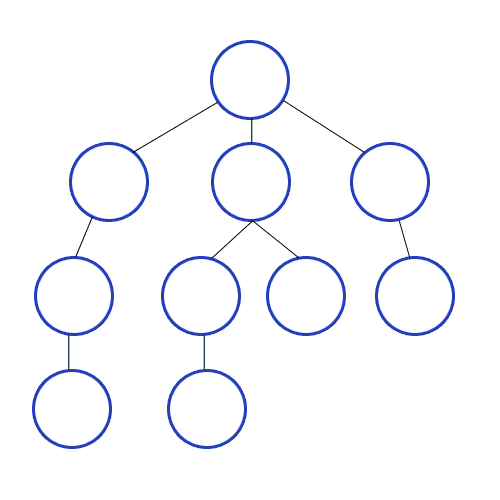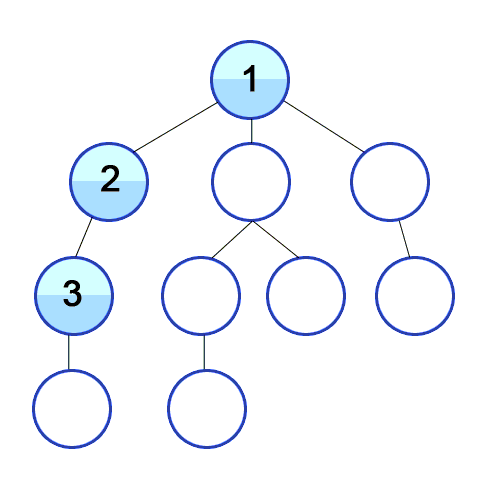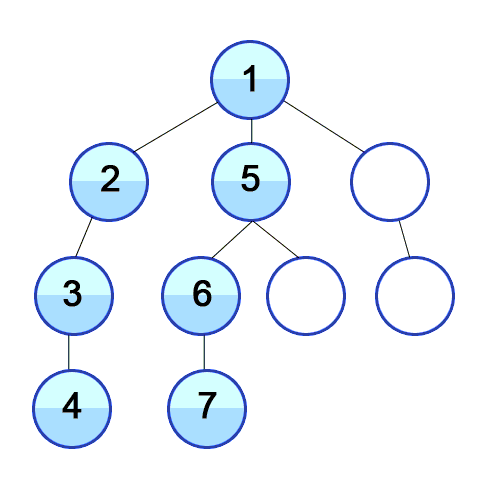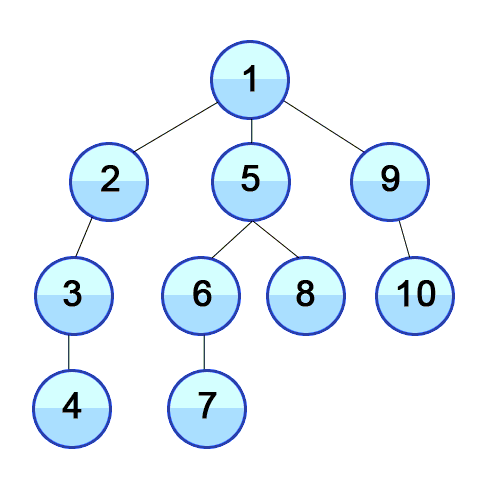
→ 4번과 인접한 노드가 없으므로 이전 노드로 이동 (4->3->2->1)
→ 1번과 인접한 남은 노드 중 가장 왼쪽에 있는 5번 노드로 이동
→ 5번 노드와 인접한 6,8번 중 왼쪽에 있는 6번 노드 탐색
→ 6번 노드와 인접한 7번 노드를 탐색한다
→ 7번과 인접한 노드가 없으므로 이전 노드로 이동 (7->6->5)
→ 5번 노드와 인접한 노드 중 방문하지 못했던 8번 노드 방문
→ 이전노드 (8->5->1) 로 이동하여 남은 9번 노드 방문
→ 9번의 인접 노드인 10번 노드 방문

그림을 보면 느낌이 오겠지만,stack을 사용해서도 구현이 가능하고 재귀 형태로도 구현이 가능하다!
효율면에서는 stack이 좀 더 좋지만, 재귀가 구현이 좀 더 쉽고 빠르다.

DFS 코드 구현 (JS Stack 버전)

우선 해당 dfs 코드를 사용하기 위해선 graph가 필요한데,
해당 보기 그래프를 리스트로 만들어보면

const graph = [[],[2,5,9],[1,3],[2,4],[3],[1,6,8],[5,7],[6],[5],[1,10],[9]]
// 리스트 자리수 : 연결된 노드
// 1번 노드 : [2,5,9] 번 노드와 연결

해당 형태를 통해 인접리스트 형태의 그래프를 만들 수 있다.

function dfs(graph, startNode){
	const visited = [] // 방문한 노드들 
    let needVisit = [] // 방문이 필요한 노드들 
    
    needVisit.push(startNode) // 방문 시작할 노드 
    
    while(needVisit.length !==0){ // 방문할 노드가 존재한다면
    const node = needVisit.pop(); // DFS는 stack 사용 => LIFO(후입 선출)구조 
    if(!visited.includes(node)){ // 해당 노드에서 방문 한 적 없는 노드라면
    	visited.push(node) //  방문 노드 처리 
        const nodes = graph[node].slice().sort((a, b) => b - a); // 복사 후 내림차순 정렬
        needVisit.push(...nodes);// 뒤에 추가 LIFO(후입 선출) 
     }
    }
   return visited;
}

dfs(graph, 1)

방문 시작할 때 :visited = [], needVisit = [1]
→ 방문할 노드 존재 (while문으로 들어감) : visited = [], needVisit = [1]
→ DFS는 stack 사용 (LIFO(후입 선출)구조) : node = 1 , visited = [], needVisit = []
→ 방문 노드 처리 -> visited = [1] needVisit = []
→ 복사 후 내림차순 정렬 ->nodes = [9,5,2], visited = [1], needVisit=[]
→ 뒤에 추가 LIFO(후입 선출) -> visited = [1], needVisit=[9,5,2]

→ 방문할 노드 존재 (while문으로 들어감) : visited = [1], needVisit = [9,5,2]
→ DFS는 stack 사용 (LIFO(후입 선출)구조) : node = 2 , visited = [1], needVisit = [9,5]
→ 방문 노드 처리 -> visited = [1,2] needVisit = [9,5]
→ 복사 후 내림차순 정렬 ->nodes = [3,1], visited = [1,2], needVisit=[9,5]
→ 뒤에 추가 LIFO(후입 선출) -> visited = [1,2], needVisit=[9,5,3,1]

→ 방문할 노드 존재 (while문으로 들어감) -> visited = [1,2], needVisit=[9,5,3,1]
→ DFS는 stack 사용 (LIFO(후입 선출)구조) : node = 1 , visited = [1,2], needVisit=[9,5,3]
→ 이미 방문 했으므로 다시 시작
.
.
.
이런 구조로 흘러가게 된다.

DFS 코드 구현 (JS 재귀 버전)

function dfs(graph,node,visited){
	if(!visited.includes(node)){
    	visited.push(node); // 현재 노드 방문 
    
    for(let n of graph[node]){ 인접 노드 
    	dfs(graph,n,visited); //인접 노드 재귀 호출 
     }
    }
    return visited;
}

1단계: dfs(graph, 1, [])
방문: 1 → visited = [1]
인접 노드 순회: [2, 5, 9]
2단계: dfs(graph, 2, [1])
방문: 2 → visited = [1, 2]
인접 노드: [1, 3]

dfs(graph, 1, [1,2]) → 이미 방문, 무시
dfs(graph, 3, [1,2]) 호출
3단계: dfs(graph, 3, [1,2])
방문: 3 → visited = [1,2,3]
인접 노드: [2, 4]

dfs(graph, 2, ...) → 이미 방문
dfs(graph, 4, ...) 호출
4단계: dfs(graph, 4, [1,2,3])
방문: 4 → visited = [1,2,3,4]

인접 노드: [3] → 이미 방문, 종료

이후 재귀가 되돌아가서 1의 다음 인접 노드인 5에 대해 재귀 호출됨:
5단계: dfs(graph, 5, [1,2,3,4])
방문: 5 → visited = [1,2,3,4,5]
인접 노드: [1, 6, 8]

dfs(graph, 1, ...) → 이미 방문

dfs(graph, 6, ...) 호출
6단계: dfs(graph, 6, [1,2,3,4,5])
방문: 6 → visited = [1,2,3,4,5,6]
인접 노드: [5, 7]

dfs(graph, 5, ...) → 이미 방문

dfs(graph, 7, ...) 호출
7단계: dfs(graph, 7, [1,2,3,4,5,6])
방문: 7 → visited = [1,2,3,4,5,6,7]
인접 노드: [6] → 이미 방문

되돌아가서 dfs(graph, 8, ...) 실행:

방문: 8 → visited = [1,2,3,4,5,6,7,8]
마지막으로 dfs(graph, 9, ...) 실행:

방문: 9 → visited = [1,2,3,4,5,6,7,8,9]