[Algorithm]boj 1018

1018번

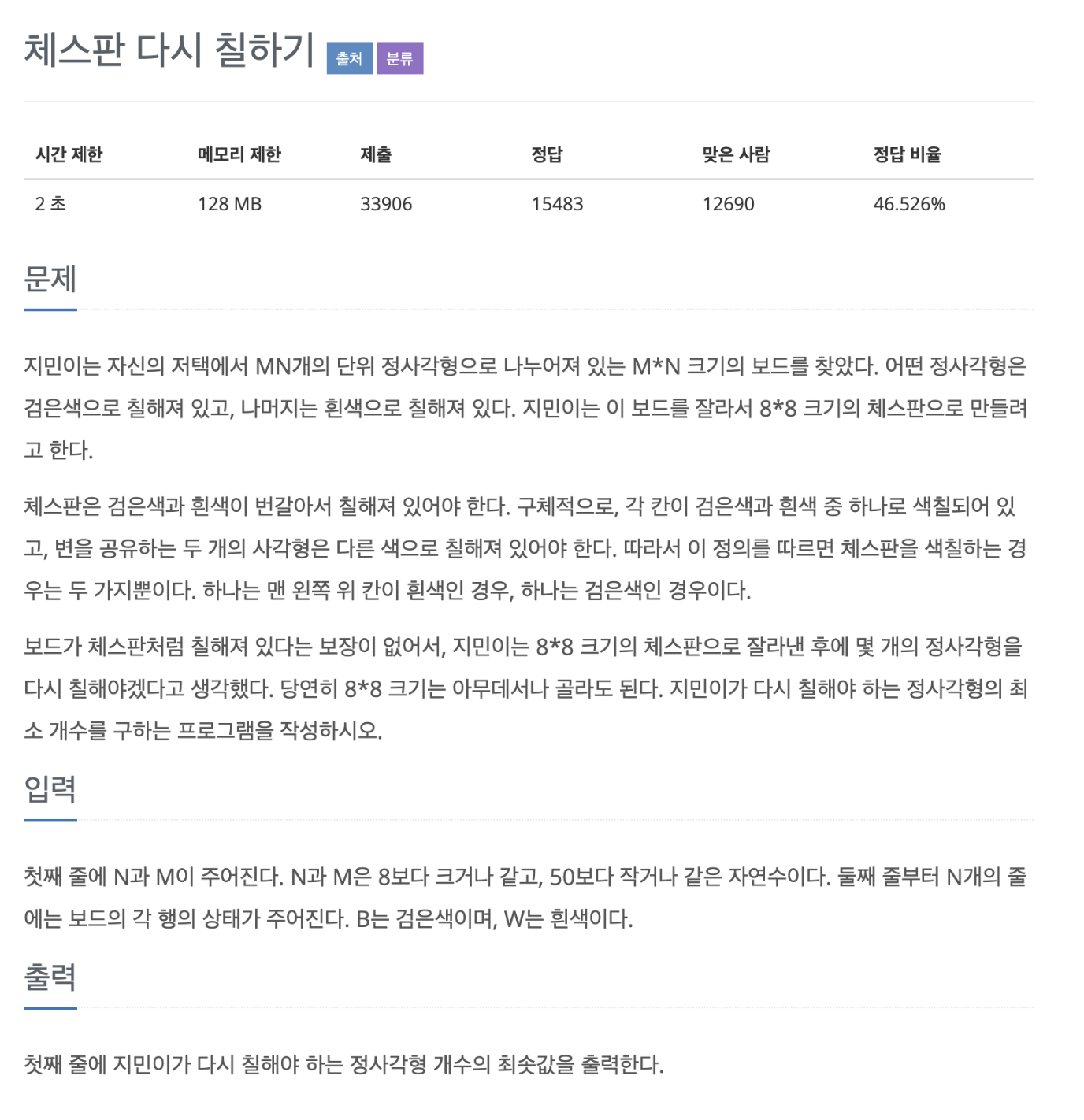
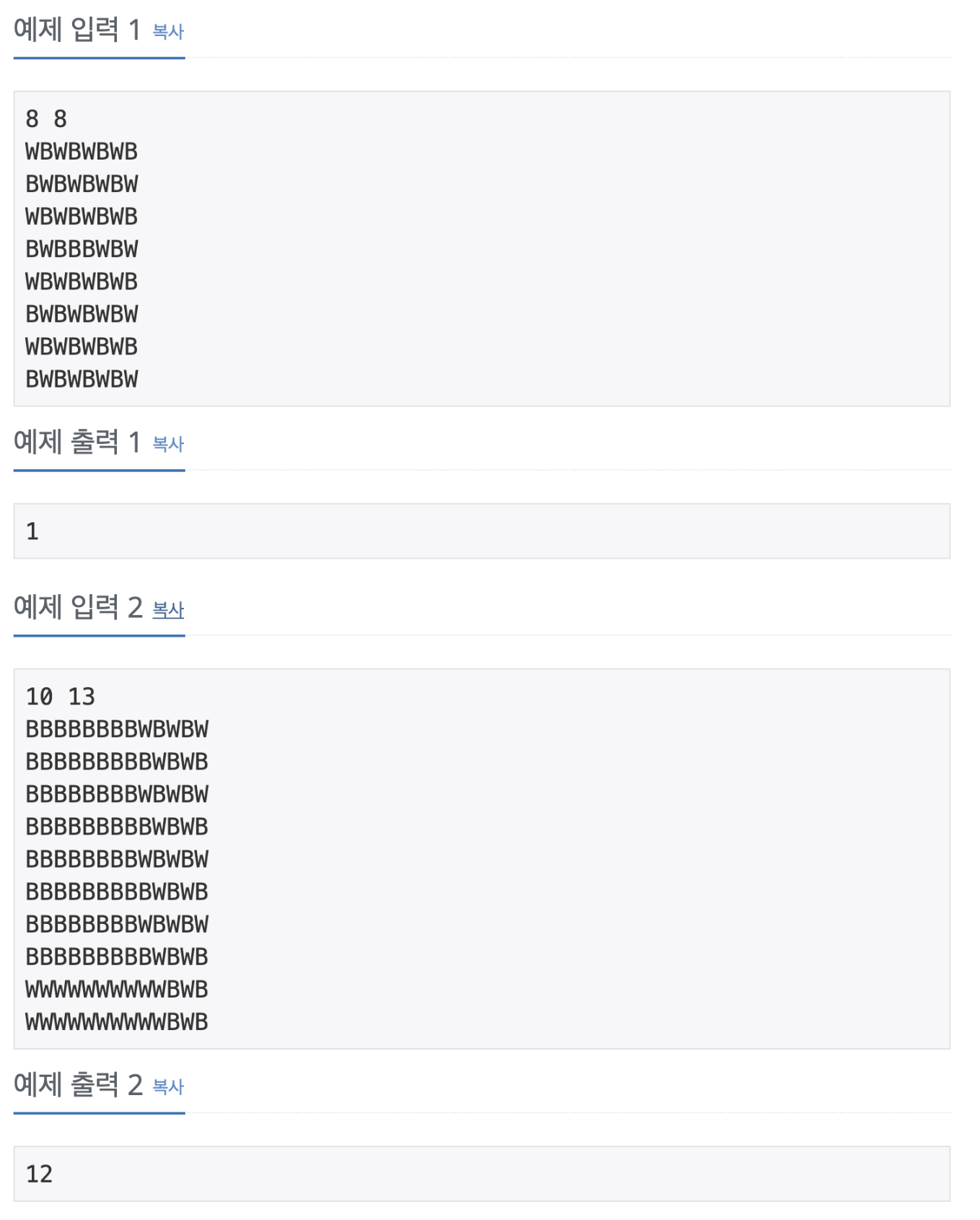
• N M 크기의 체스판을 8 8로 잘라서 정상적인 체스판으로 만들기 위한 최소한의 색 바꾸는 횟수를 구하는 문제

• 자를 수 있는 8 by 8 크기의 배열을 전부 다 해봐야한다.

• 8 by 8로 만들 수 있는 체스의 경우의 수는 다음과 같이 두 가지이다.

  

• 우선 8 by 8로 자르고, 자른 체스판을 순회하면서

  • 만약 짝수의 색이 입력한 color와 다르다면 갯수를 세준다.
  • 반대로, 홀수의 색이 !color 와 다르다면, 즉 color와 같다면 갯수를 세준다.
  • 어차피 색깔은 둘중 하나이므로 색깔에 큰 의미부여하지 않아도 된다.

• 그리고 나서 반대쪽 체스판도 해봐야 하므로, 이번엔 위 color값의 반전값을 넣어서 동일하게 실행해준다.

• 그 둘 값의 최솟값을 구해주면 된다.

• 최대 입력 값이 50개 이므로 최대 연산 횟수는 다음과 같다
  - (50 - 8) (50 - 8) 8 8 2 = 22만정도 이다
  - 50에서 8을 빼는 이유는 체스판의 시작위치가 43이 되면 더 이상 자를 수 없기 때문이다.
  - 앞의 두개는 체스를 자르는 연산, 8 * 8 는 체스를 순회하는 연산, 그리고 나머지 2는 두 종류의 체스가 있으므로 두 번의 연산까지의 곱이다.

  #include <iostream>
  
  using namespace std;
  int N, M;
  int chess[50][50];
  
  int go(int i, int j, int color)
  {
  	int sum = 0;
  	for (int r = i; r < i + 8; r++)
  	{
  		for (int c = j; c < j + 8; c++)
  		{
  			if (c % 2 == 0 && color != chess[r][c])
  				sum++;
  			else if (c % 2 == 1 && color == chess[r][c])
  				sum++;
  		}
  		color = !color;
  	}
  	return (sum);
  }
  
  int main(void)
  {
  	char temp;
  	cin >> N >> M;
  	int res = 987654321;
  	for (int i = 0; i < N; i++)
  		for (int j = 0; j < M; j++)
  		{
  			cin >> temp;
  			if (temp == 'B')
  				chess[i][j] = 0;
  			else
  				chess[i][j] = 1;
  		}
  	for (int i = 0; i + 7 < N; i++)
  	{
  		for (int j = 0; j + 7 < M; j++)
  		{
  			res = min(go(i, j, 0), res);
  			res = min(go(i, j, 1), res);
  		}
  	}
  	cout << res;
  }