Loss Function
-
손실함수 Loss function == 비용함수 Cost function == 목적함수 Object function == 오차함수 error function == criterion 등등 다양한 명칭으로 불리지만 의미하는 것은 모두 같다.
-
손실값 Loss는 model의 잘못된 예측에 대한 penalty라고 할 수 있다.
즉, 우리 model의 결과값 가 실제 와 얼마나 다른지를 나타내는 값이다. -
만약 모델의 예측이 완벽할 수록 loss는 0에 가깝고 반대라면 loss는 커질 것이다.
먼저 를 알아보기전 에 대해서 간단히 짚고 넘어가자.
우리가 간 차이,거리를 구할 때 사용하는 것이 바로 이다.
- 원점 벡터 와 을 구하면 의 길이를 구할 수 있고,
- 원점이 아닌 벡터 와 의 을 구하면 두 벡터의 차이를 알 수 있다.
와 을 계산해보자.
= 라고 하면
= 으로 계산할 수 있다.

위는 의 n에 따라 좌표 공간에서 을 시각화하여 표현한 것이다.
의 벡터가 있을 때 = 1 을 표현한 것이다.
-
=> = = = 1
-
=> = = 1
||x|| 와 같이 아래첨자가 생략된 표기는 L2 norm을 의미한다.
-
: 실제로는 norm을 의미하는 것은 아님. vector의 총 길이(차원)를 나타냄.
- 중 0이 아닌 원소의 수
-
: 맨하탄 거리
-
: 유클리드 거리
- 에 비해 오차의 제곱을 하기 때문에 큰 오차(outlier)에 대해 민감하다.
-
:
- 과 동일 즉, 가장 큰 값 를 값으로 사용하겠다.
- 의 n이 증가할 수록 값 는 큰 값 에 영향을 많이받는다.
- 가면 큰 값 말고는 무시되므로 는 max()와 동일하게 작용한다. (증명)
& 을 으로 사용할 때
이를 weight decay라고 하며 기존의 손실함수에 weight 벡터의 을 추가한다.
목적 : 모델의 weight가 너무 커지면 몇몇 feature에 의존하게 된다.
따라서 특정 weight가 과도하게 커지지 않게 큰 weight는 작아지도록 하는 역할을 수행한다.
-
=
-
미분 시 :
-
즉, weight의 부호만 1 or -1만 남는다. * 이므로 weight의 크기에 상관없이 상수항을 더하고 빼는 효과이다.
-
sparse feature를 사용하는 model에서 L1 reg를 쓰면 불필요한 feature(이상치)에 대응하는 weight를 0으로 만드는 Feature selection 효과도 볼 수 있다.
-
-
=
- 미분시 :
- 와는 다르게 weight의 크기에 따라 을 빼주므로 더 빠르게 감소시킨다.
- 또한 은 불필요한 feature(이상치)에 대응하는 weight를 0에 가깝게 만들지만 결코 0이 될 순 없음 (w크기에 따라 감소되므로, L1은 상수만큼 감소) -> 더 뛰어난 일반화 성능
MSE는 거리기반 손실함수로 과 같은 의미이다.
MAE는 으로 절대값 평균
는 데이터의 실제 label이며 는 model의 출력값이다.
이때 와 는 or 가 될 수 있다.
Likelihood 우도
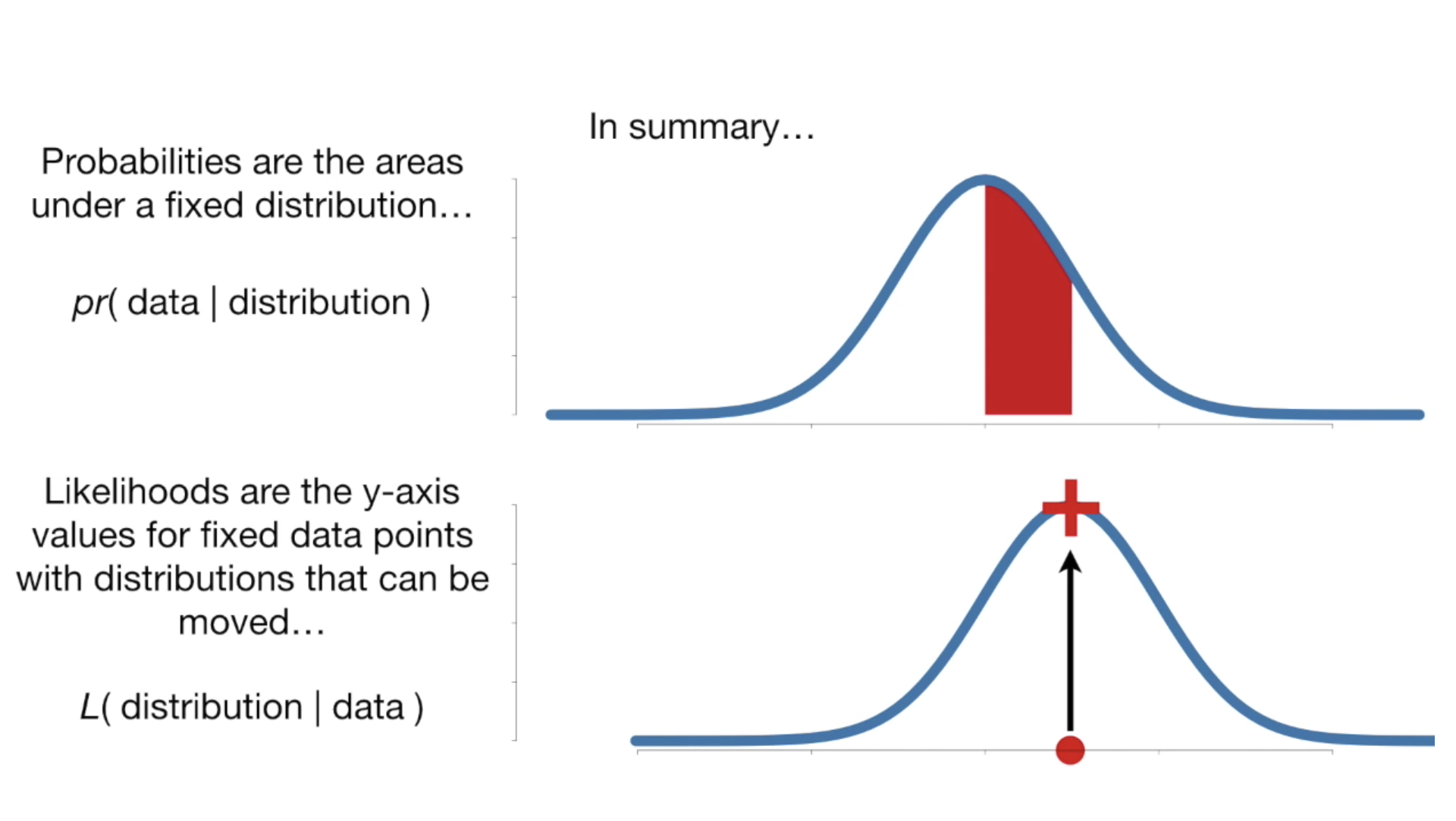
- 확률 : 확률분포가 주어졌을 때 x값(분포)를 알면 y가 일어날 확률을 알 수 있다.
- 우도 Likelihood : 확률과는 반대로 주어진 관측 데이터에 대해 확률분포를 추정한다.
- 우도가 높을수록 주어진 관측데이터를 잘 표현한다.
- 우도가 높다 = 높은 엔트로피 = 정보가 많다 = 모델이 사용할 정보가 많다.
Maximum Likelihood Estimation 참고
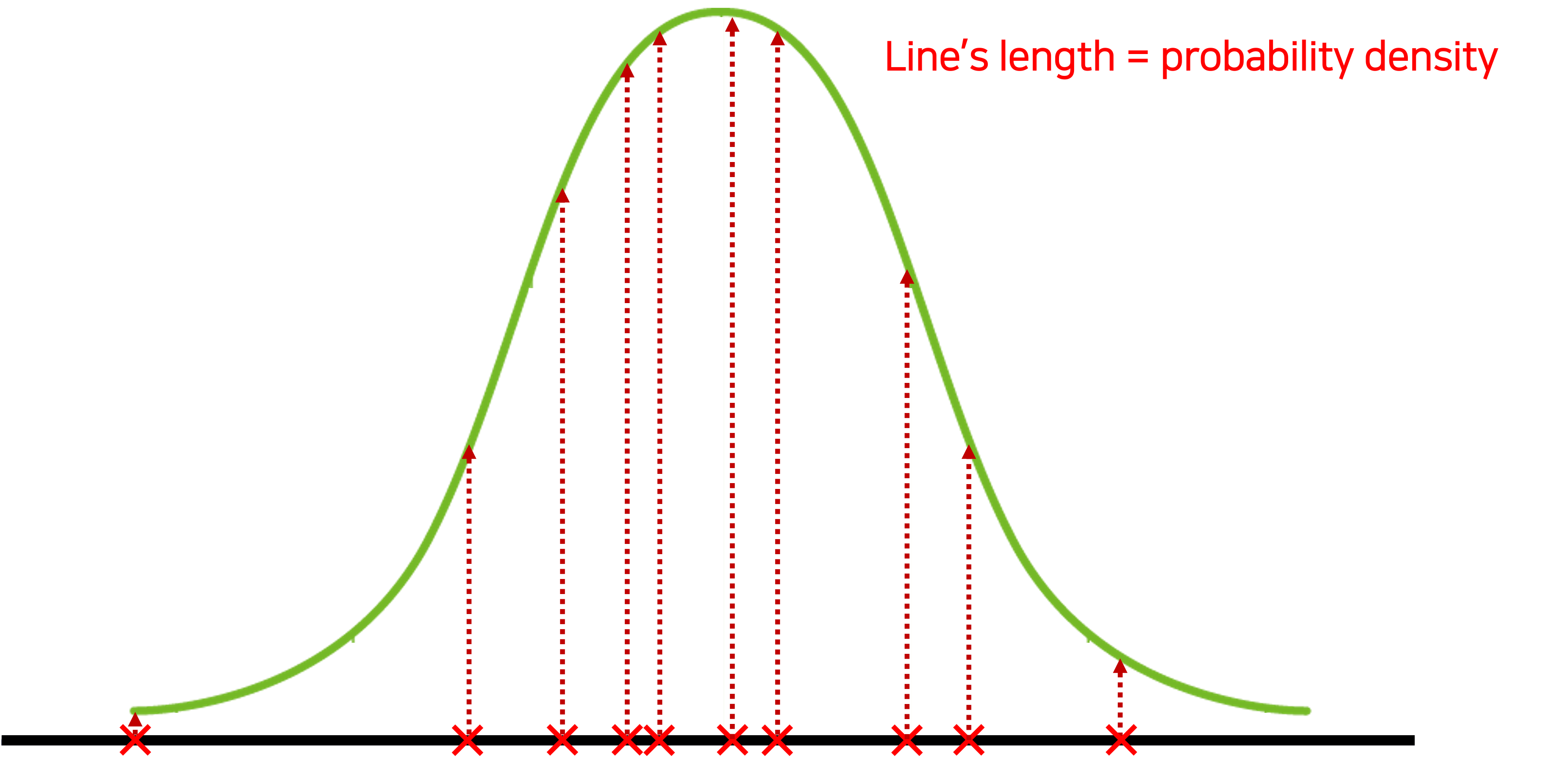
주어진 샘플로 최적의 데이터셋 분포를 나타내기 위해선 그림의 점선 길이(;확률)들의 곱이 최대가 되어야할 것이다.
이때 점선 길이들의 곱을 Likelihood라고 하며 Likelihood를 최대로 하여 최적의 분포를 찾아내는 것이 바로 Maximum Likelihood Estimation이라 할 수 있다.
는 데이터셋
가능도는 위에서 본 것 처럼 확률의 곱으로 표현된다.
따라서 Log 씌워서 표현할 수 있다.
- 는 정보량을 나타낸다고 할 수 있음.
- Log Likelihood 장점
- 샘플의 숫자가 많아진다면 Likelihood는 매우 작아질 수있음. -> 언더플로의 위험
- 곱셈연산보다 덧셈연산이 빠름
- 는 0~1사이의 값일 텐데 0에 가까울 수록 -에 발산 (-붙으므로 ) 1에 가까울수록 0에 가까워짐
- model학습 시 Loss의 를 위해 Negative log likelihood를 주로 사용하게 됨
Cross-Entropy 크로스 엔트로피
-
직관적으로 Cross-Entropy는 두 확률분포의 차이정도(같은 확률 분포라고 0은아님)
- 따라서 KL 구할때 CE(p,q) - CE(p,p)
-
크로스 엔트로피 수식
-
두 확률 분포 p와 q의 차이를 계산하는데 사용 즉, 오차계산
-
는 실제 레이블(정답 벡터) , 는 모델이 예측한 확률 분포 즉, =
-
즉 확률의 기댓값이고 을통해 likelihood의 기댓값을 구하는거임!!!
- 에만 를 씌우고 에는 안씌움 보통 는 연산 되있는 걸 의미
-
- 직관적으로 을 이해해보자.
- 정보이론관점에서 값이 낮으면 확률상 희귀한 상황이다. 그럼 값은 높아지고 실제 가 실제로 높은 상황이라면 은 매우 의미있는 결과란 뜻이다.(가 크다.)
- 즉, 크로스 엔트로피란 어원은 실제 y와 예측 y의 정보량(엔트로피)의 곱(크로스)에서 온 것을 알 수 있따.
- (트레이드 오프에서 곱이 최대가 되려면 교차점이 되는 것 처럼)CE값이 최대가 되려면 실제 y와 예측 y 확률이 0.5 0.5가 되야할 것이다. uniform distribution에서 CE 최대 (연속확률분포에선 정규분포시 최대)
- 모든 가능한 사건이 하나의 결과만 나온다면 Cross-Entropy는 0이됨. 두 분포가 완전히 동일할 때
- 동일한 분포라 하면 [0,0,0,1] , [0,0,0,1]이 되어야 한다. [0.1,0.2,0.3,0.4][0.1,0.2,0.3,0.4]는 각 사건이 일어날 확률이 각각 있음 따라서 같은 확률분포가 아님! (중요)
- CE 미분값 :
Binary Cross-Entropy
Multi-labeling 에서 사용0 or 1을 분류할 때 사용
Cross-Entropy에 y=0일때와 y=1인 경우를 단순히 더한 것임
-
예측값이 단일 항목으로 이루어져있다면 (ex, [0.5])
- 단순 이진 분류이므로, 목적함수로 Binary Cross Entropy 를 사용
-
예측값이 여러개의 항목으로 이루어져있으며, 각 항목의 확률 합이 1 이 넘어간다면 (ex, [0.7, 0.6, 0.4])
- 멀티 이진 분류이므로, 목적함수로 Binary Cross Entropy 를 사용
- 이 문제는 out of distribution과 같이 각 feature가 임계값을 넘는지 판단할 때 사용할 수 있다.
- 즉, softmax를 사용했다면 class가 정해지므로 Cross Entropy를 사용하지만 최종 representation일 땐 Cross Entropy를 바로 사용하면 안된다.
-
예측값이 여러개의 항목으로 이루어져있으며, 각 항목의 확률 합이 1 이라면 (ex, [0.5, 0.2, 0.3])
- 다중 분류이므로, 목적함수로 Cross Entropy 를 사용
-
즉, 최종 feature 전체를 계산할 땐 Cross Entropy, 각각의 feature를 계산할 땐 BCE사용으로 '일단'알고있자. (확신 생기면 수정하기!!!!!!)
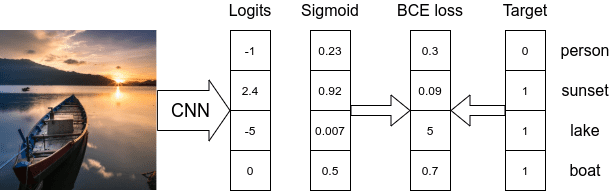
NLLLoss vs Cross-Entropy
-
Cross-Entropy = Logsoftmax(y_pred) + NLLLoss()
- 크로스엔트로피는 모델의 마지막 layer를 그냥 받는다.
- CE(y_pred,y_real)을 하면 y_pred는 Log-Softmax연산이 되고 y_real과의 NLLLoss()를 구한다.
-
NLLLoss() =
- NLLLoss()는 모델의 마지막 부분에 Log-Softmax() 연산을 해줘야 한다.
- Log-softmax연산이 된 y_pred와 class를 나타내는 y_real와 NLLLoss(y_pred,y_real)을 해주면 Cross-Entropy와 같은 값이 나온다.
- 이때 표현을 해준 이유는 에서 는 원핫이고 1인 값의 말고는 모두 0과 곱해짐
ps
- - 는 둘다 monotonic(단조증가) 함수이므로 큰 값 순위는 바뀌지 않음
- 따라서 Cross-Entropy를 사용하기 위해선 를 위해 Log와 확률로 나타내기 위해 softmax를 적용해야한다.
Cross-Entropy와 KL Divergence는 사실 같은 것
두 분포의 차이를 계산함
q는 실제 분포 p는 모델의 예측 분포 ,CE(,)이라고 하면
KL Divergence는 CE(p,q) - CE(p,p)이다.
즉,
KL Divergence = p와q의 크로스엔트로피 - p의 엔트로피 형식이다.
import torch
y_pred = torch.Tensor([0.7,0.8,0.3,0.4])
y_real = torch.Tensor([0.5,0.5,0.5,0.5])
kl_loss = torch.nn.KLDivLoss (reduction = 'none')
loss = torch.nn.CrossEntropyLoss (reduction = 'none')
softmax = torch.nn.Softmax()
log_softmax = torch.nn.LogSoftmax(dim=-1)
kl_v = kl_loss(log_softmax(y_pred),softmax(y_real))
cross_ent_v = loss(y_pred,softmax(y_real))
ent_v = loss(y_real,softmax(y_real))
print(f'kl-divergence : {kl_v}')
print(cross_ent_v,ent_v)
print(kl_v.sum(),cross_ent_v-ent_v)kl-divergence : tensor([-0.0322, -0.0572, 0.0678, 0.0428])
tensor(1.4074) tensor(1.3863)
tensor(0.0211) tensor(0.0211)
Distribution 분포
확률 분포는 이산확률분포와 연속확률분포로 나뉜다. 참고
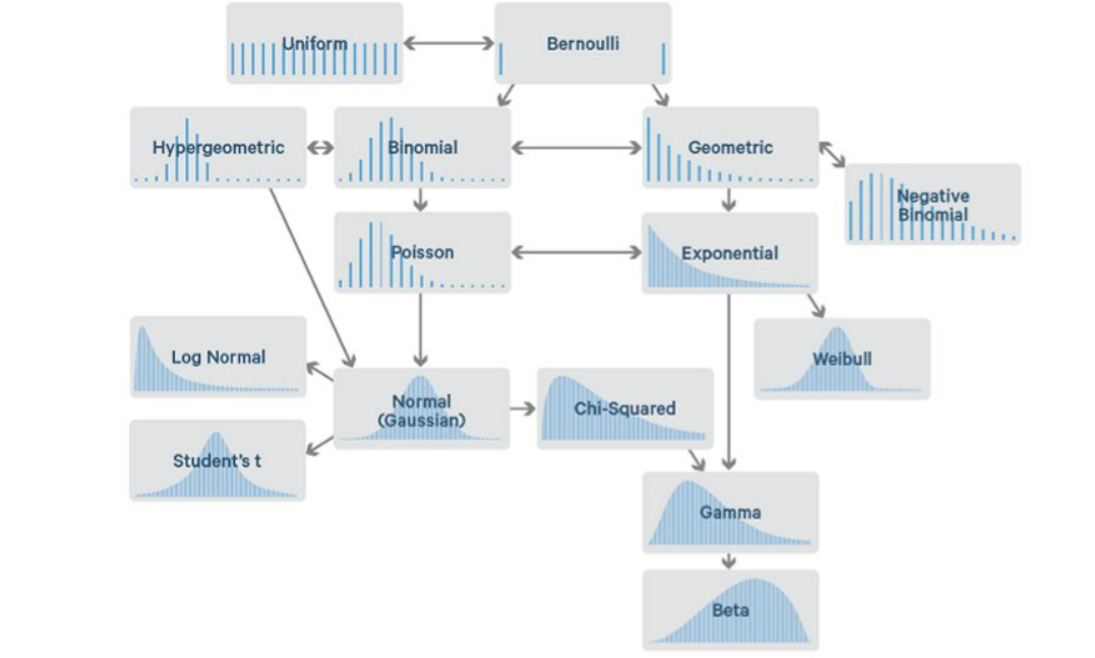
-
이산확률분포
-
이항분포(Binomial Distribution) , 베르누이분포(Bernoulli Distribution)
- 베르누이분포는 이항분포에서 n=1인 상황
-
기하분포(Geometric Distribution)와 음이항분포(Negative Binomial Distribution)
-
초기하분포(Hypergeometric Distribution)
-
포아송분포(Poisson Distribution)
-
-
연속확률분포
- 정규분포(Normal Distribution)
- 감마분포(Gamma Distribution)
- 지수분포(Exponential Distribution)
- 카이제곱분포(Chi-squared Distribution)
- 베타분포(Beta Distribution)
- 균일분포(Uniform Distribution)
적절한 loss함수
거리기반 ()을 사용할 때 주의할점!!!!
매우중요!!! 이 글을 쓰는 가장 중요한 이유임

-
왼쪽은 가우시안 분포를 유도한 수식으로 평균 와 분산 (1이며 위에서는 로 표기)가 있을 때 우리는 에 대한 확률값을 구할 수 있다.
-
양변에 log를 씌우고 이러쿵저러쿵 식을 유도하니
로 표현할 수 있다.
-
이는!!! 우리가 위에서 봤던 & 과 동일한 것을 볼 수 있다.
-
즉, 우리는 의 을 구하기위해 를 하면 된다.
-
문제에서 손실함수로 를 쓰는 이유는 은 연속확률분포를 갖는 분포를 따른다고 가정했기 때문이다!!!
-
-
오른쪽은 이산확률분포 중에서도 이항분포 중에서도 베르누이 분포를 유도한 수식이다.
- 유도식과 마찬가지로 문제로 풀기위해 를 붙임
- 이항분포는 모든 데이터가 독립시행을 가정하기 때문에 곱연산
- 우리가 풀려는 문제는 시행횟수가 1이기 때문에 베르누이 분포
- 위의 식의 은 이해하기 쉽게n개의 class 즉, 출력층 차원이라고 생각하자.
- 유도식과 마찬가지로 문제로 풀기위해 를 붙임
-
따라서 우리의 문제가 연속 or 이산 분포 (회귀 or 분류)인지 파악하고 적절한 Loss function을 선택해야한다.
- Representation Learning 또한 hidden dimension의 차원이 정해져 있으므로 이산확률 분포문제
- 뇌피셜 : 컴퓨팅자원의 한계로 hidden 가 정해진거지 사실은 연속확률분포 문제임. 다만 최대한 근사하는 것이 목적
- Representation Learning 또한 hidden dimension의 차원이 정해져 있으므로 이산확률 분포문제
Softmax & Sigmoid & Logit
- sigmoid는 대표적인 Logistic 함수이다.
- 입력에 상관없이 0~1로 출력
- ex)인구 증가 모델로 많이 설명됨 - 폭팔적인 성장 후 더딘 성장
- softmax에서 를 쓰는이유는 제일 큰거에만 몰빵 , 나머지는 0에 가깝게
- 즉, 같이 큰 값에다 많은 가중치를 줌
