[알고리즘] Topological Sort

Topological Sort

• 입력은 DAG(Directed Acyclic Graph)이다.
• 모든 Directed Edge가 왼쪽에서 오른쪽으로 향하도록 노드를 정렬한다.

DAG에는 indegree가 0인 게 적어도 하나 존재한다.
그래야 Cycle이 없을 수 있기 때문이다.

알고리즘

• DAG G로 부터 indegree가 0인 노드 v를 지운다.
• 남은 그래프를 G'이라고 할 때 이 그래프도 여전히 DAG이다.
• 만약 G에서 Topological Sort가 가능했다면 G'에서도 가능하다.

v는 indegree가 없고, 모든 엣지는 왼쪽에서 오른쪽으로 향하도록 정렬했으므로 뒤 순서의 노드 중 v로 향하는 엣지를 가진 노드는 없을 것이기 때문이다.

Event Queue

Event Queue를 사용하면 더 빠르게 할 수 있다.

1. indegree를 계산한다.
2. indegree가 0인 것들을 Queue에 넣는다.
3. Queue로부터 v를 꺼낸다.
4. v와 연결된 노드들의 indegree를 -1 해준다.
5. 이후 다시 indegree가 0이 된 노드들을 Queue에 넣는다.

노드 v를 지웠을 때 indegree가 0이 될 수 있는 애들은 v와 연결되어 있었던 노드들 뿐임을 이용하여 Event Queue를 적용할 수 있었나보다.

DFS & Post Number

조금 더 빠른 방법은 DFS와 Post Number를 이용하는 것이다.

1. DFS를 진행한다.
2. 노드에 Post Number를 붙인다.
3. 내림차순으로 PostNumber를 출력한다. (Sort 필요)
   또는 Post 번호를 계산하면서 출력해도 되는데 거꾸로 출력하게 된다.

3번의 결과는 위상정렬의 결과와 같다.

참고

1. Post 번호의 특징
   - 트리의 아래 쪽으로 갈 수록 작아지고, 왼쪽으로 갈 수록 작아진다.
2. Topological Sort 후의 DAG에서는 Shortest Path, Longest Path를 찾는 게 더 쉬워진다.

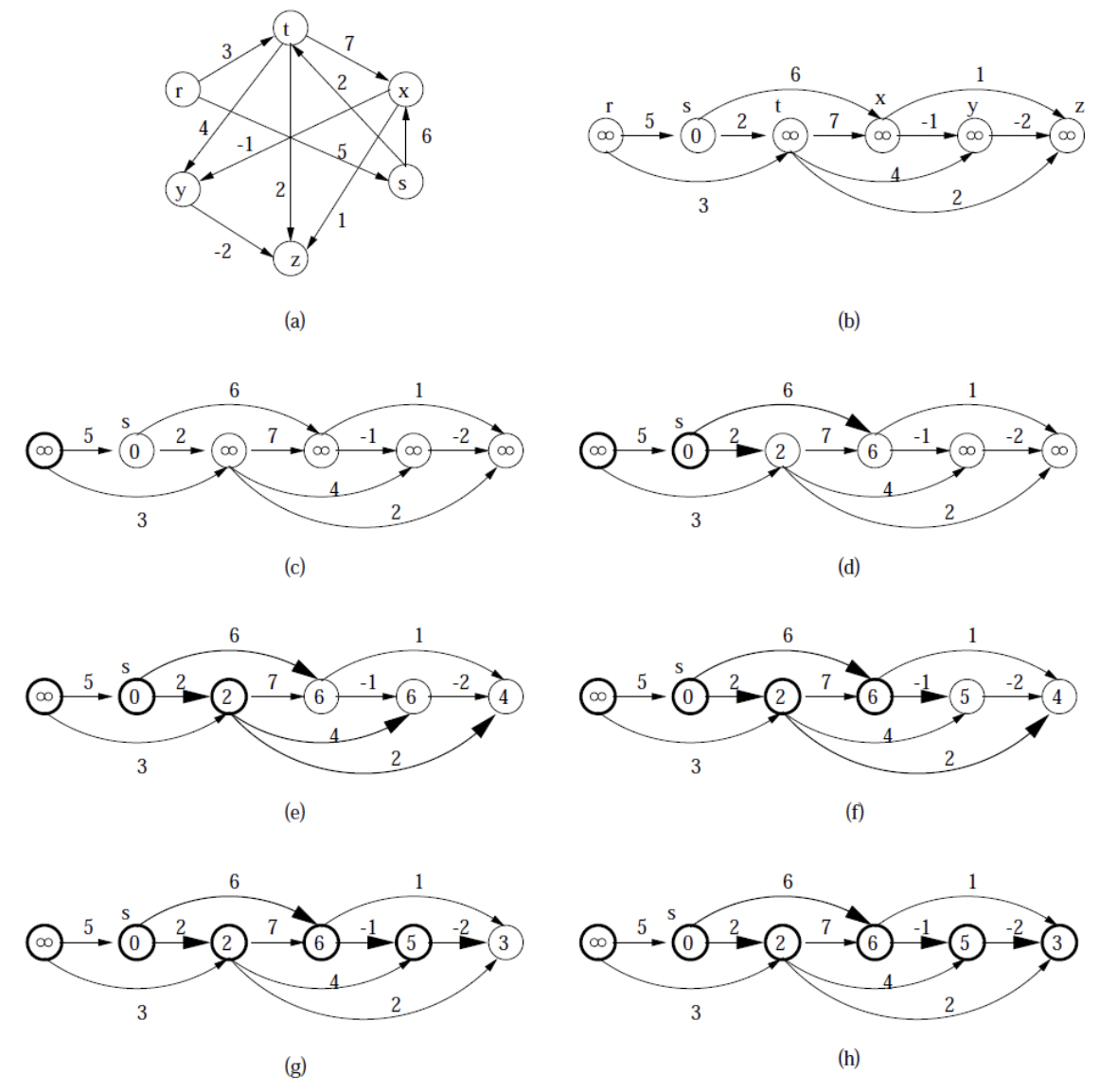
아래 사진은 Topological Sort 후 Shortest Path의 예시