Strongly Connected Component 란 노드들 중 가장 큰 서브 집합을 의미한다.
같은 SCC에 속하는 두 정점은 서로 도달이 가능하다는 특징이 있다.
따라서 사이클이 발생하는 경우 무조건 SCC에 해당한다.
방향 그래프에서만 의미가 있는데, 무방향 그래프인 경우 그 그래프 전체는 무조건 SCC이기 때문이다.
DFS 트리와 간선의 분류
- DFS 트리란 어떠한 그래프에서 DFS하는 과정을 트리로 나타낸 것이다.

노드 왼쪽에 적힌 숫자는 discovery time으로 해당 정점을 방문한 순서이고,
finish time은 해당 정점의 모든 자식을 방문하고 그 정점을 빠져나간 순서이다.
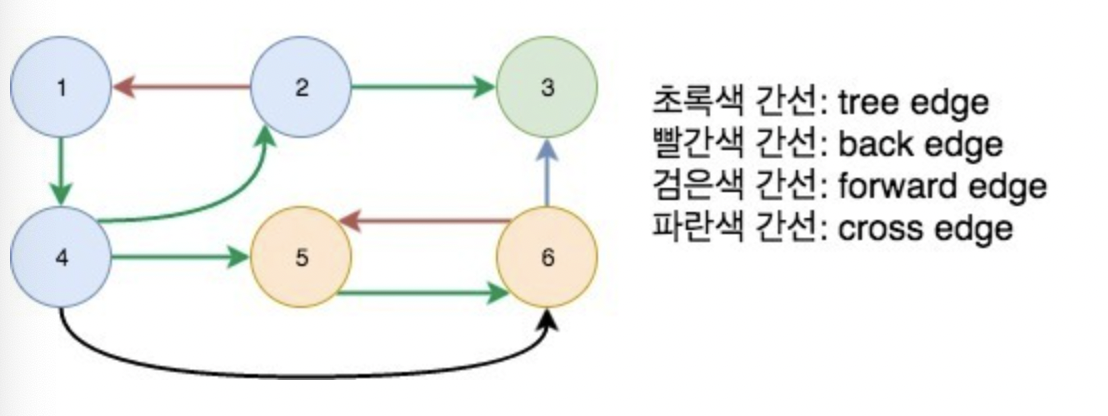
이러한 DFS 통해 그래프의 간선들을 다음과 같이 분류할 수 있다.
1. Tree Edge
- 그래프의 간선 중 DFS 트리에 속하는 간선이다.
- 이 경우 노드 u,v가 있을 때 dt[u] < dt[v], ft[v] < ft[u] 이다.
- Back Edge
- 그래프의 간선 중 DFS 트리에서 v가 u의 조상인 간선이다.
- 이 경우 dt[v] < dt[u] 이고, ft[u] < ft[v] 이다.
- Forward Edge
- 그래프의 간선(u->v) 중에서, DFS트리에서 u가 v의 조상인데 tree edge에는 속하지 않는 간선이다.
- 이 경우 dt[u] < dt[v] 이고, ft[v] < ft[u] 이다.
- Cross Edge
- 위의 3가지 간선에 모두 해당하지 않는 간선이다.
- 그래프의 간선(u->v)들 중에서 DFS트리에서 u가 v의 조상도 아니고, v가 u의 조상도 아닌 경우이다.
- 이 경우 dt[u] > ft[v] 이다. (즉 나중에 방문된 거면 finish time도 늦다.)
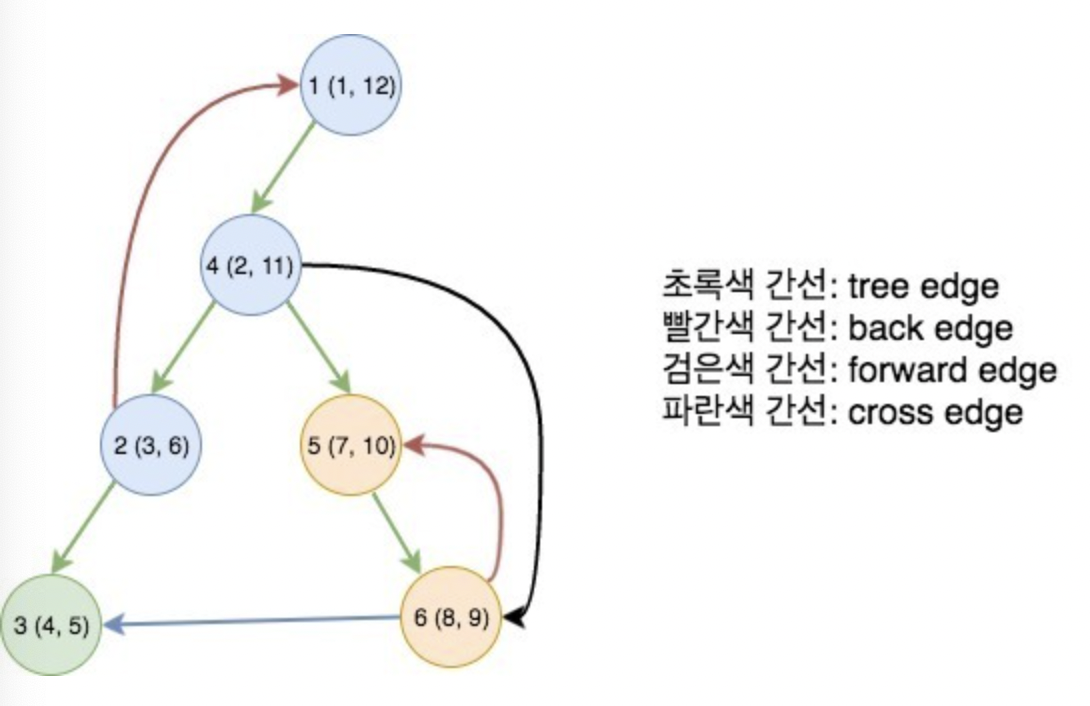
SCC를 찾는 방법
1. DFS를 수행한다.
2. 여러 개의 Tree들과 Cross Edges(to the left)가 생긴다.
3. 하나의 Tree는 여러 개의 SCC를 포함할 수 있다. (하나의 SCC는 하나의 Tree에만 속할 수 있다.)
각 Tree에서도 하나의 SCC만 가지도록 분리하는 알고리즘
1. 그래프를 DFS 하면서 Post() Number를 붙인다.
2. 그래프에서 모든 간선의 방향을 반대로 바꾼다.
3. Post() Number가 큰 정점부터 DFS를 한다. 이 결과는 각각 하나의 SCC이다.
Post() Number가 가장 큰 정점은 어떤 트리에서 항상 루트 노드이다.
따라서 모든 간선의 방향을 반대로 바꾸면 루트 노드를 포함하는 SCC에서 다른 SCC로 내려갈 수 없다.
그렇게 해서 SCC를 분리할 수 있게 된다.
이러한 그래프가 있었고,
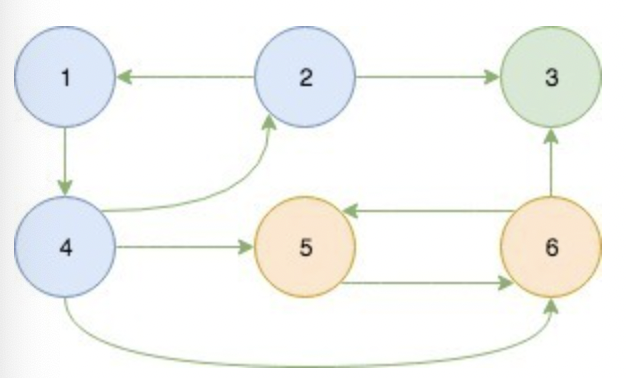
다음과 같이 DFS Tree를 만들었다.
1-4-2-3-.. 와 같은 순서로 트리의 노드를 방문했었다.
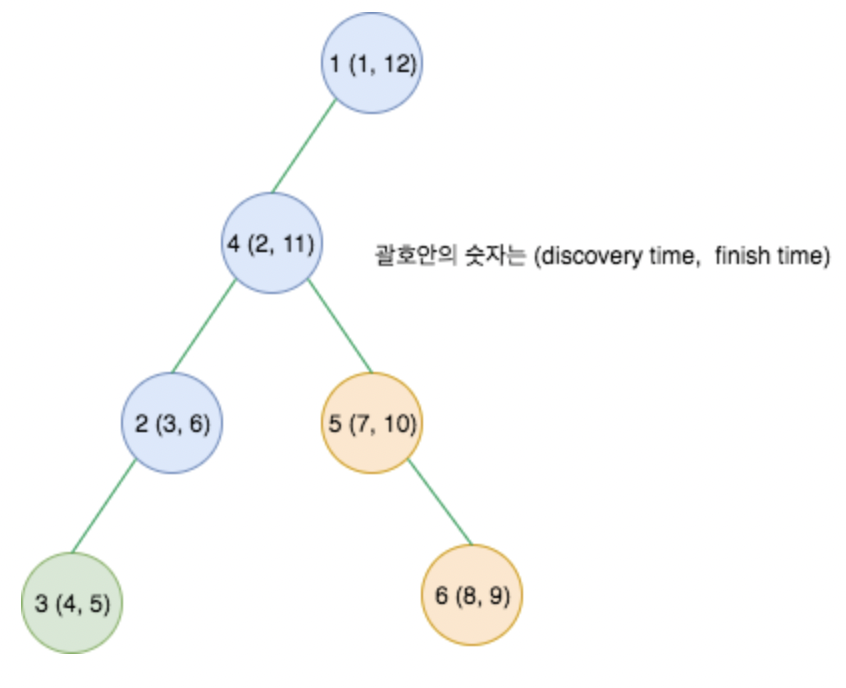
초기 그래프에서 모든 간선의 방향을 반대로 바꾼 역방향 그래프를 만든다.
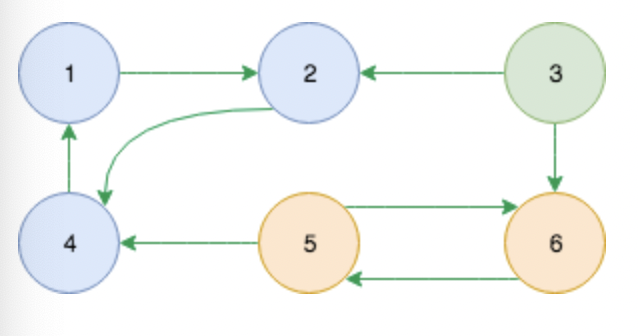
그리고 노드의 Post number가 큰 것부터 다시 DFS를 해보면,
역방향이 된 간선들 때문에 1-2-4를 방문하고 더 이상 갈 곳이 없게 된다.
이렇게 SCC를 발견할 수 있다.
