PMI를 활용한 word-context 행렬에 SVD와 같은 행렬분해를 수행하면 SGNS를 통해 학습된 word embedding과 유사한 결과를 얻을 수 있다는 것을 보인 논문입니다.
[Abstract]
해당 논문에서는 SGNS(Skip-gram with Negative Sampling)을 분석하고, SGNS가 특정 상수만큼 평행이동한 단어와 문맥 쌍의 PMI(Pointwise Mutual Information)을 원소로 갖는 word-context 행렬의 분해임을 보입니다. 논문에서는 sparse Shifted Positive PMI word-context 행렬을 활용하여 단어를 표현하는 것이 성능이 좋다는 것을 보여줍니다.
1. Introduction
자연어처리, 자연어이해 분야의 많은 task에서 하나의 단어를 하나의 symbol로 다루는 것이 아닌, 여러 단어들 사이의 유사성과 차이점을 반영함으로써 좋은 결과를 얻을 수 있었습니다. 유사한 문맥의 단어는 유사한 의미를 지닌다는 분포 가설(distributional hypothesis)이 이런 경향의 기반이 되었습니다.
Word-context 행렬 M에서 각 row는 단어와 관련이 있고, 각 column은 단어가 등장한 문맥과, 행렬의 원소 M_ij는 단어와 문맥의 연관성을 측정하는 지표와 관련이 깊습니다. 단어는 행렬 M의 row나 행렬 M을 차원축소한 결과의 row로 표현합니다.
근래에 들어 neuraal-network lanugage modeling으로부터 영감을 받은 학습 방법을 활용하여 단어를 dense vector로 표현하는 큰 변화가 생겼습니다. 이런 방법들을 neural embeddings 또는 word embeddings라고 부릅니다. 대표적인 방법으로 SGNS가 있습니다. 학습의 목적이 distributional hypothesis를 따른다는 것(유사한 단어는 가깝게 유사하지 않은 단어는 멀게)이 명백하지만 해당 알고리즘이 얼마나 최적화 되었는지, 어째서 해당 단어 representation이 좋은 방식인지에 대한 이유에 대해서는 거의 알려진 것이 없습니다.
해당 논문에서는 neural-inspired word embeddings의 이론적 이해로 확장하는 것을 목표로 합니다. 그 중 SGNS의 학습 방법이 weighted matrix factorization으로 볼 수 있다는 것을 보이고 SGNS의 목적이 shifted PMI matrix(특정 상수만큼 빼준 word-context PMI matrix)를 분해하는 것과 동일하다는 것을 보입니다.
마지막으로, 해당 논문은 shifted PPMI matrix에 SVD를 수행하는 단순한 spectral 알고리즘을 제안합니다. 해당 알고리즘은 SGNS와 shifted PPMI 행렬의 성능을 뛰어넘었습니다.
2. Background: Skip-gram with Negative Sampling(SGNS)
해당 논문의 출발점은 SGNS입니다.
Setting and Notation
skip-gram model은 말뭉치(V_w)의 원소 w와 w의 문맥(V_c)의 원소 c를 가정합니다. 단어 w는 특별한 라벨이 붙어 있지 않은 수십 억개의 단어로 이루어진 말뭉치에서 뽑힙니다. 단어 w의 문맥들은 window size L에 대해 단어 w 앞 뒤로 L개의 단어들을 의미합니다. 해당 논문에서는 단어 w와 문맥 c의 쌍 집합을 D로 표현합니다. #(w,c)는 집합 D에서 (w,c)가 등장한 횟수를 의미하며, #(w)는 집합 D에서 w가 등장한 횟수, #(c)는 집합 D에서 c가 등장한 횟수를 의미합니다.
각 단어 w들은 d차원 vector w-와 관련이 있고, 문맥 c 역시 d차원 vector c-와 관련이 있습니다. vector w-는 |V_w| d 차원 행렬 W의 row이고, vector c-는 |V_c| d 차원 행렬 C의 row 입니다.
SGNS's Objective
P(D=1|w,c) 는 (w, c)가 D로부터 나왔을 확률을 의미하고, P(D=0|w,c) 는 (w, c)가 D로부터 나오지 않았을 확률을 의미합니다. 확률분포함수는 아래와 같이 표현할 수 있습니다.

Negative sampling의 목적은 실제 관측된 (w, c) 쌍에 대해서 P(D=1|w,c) 값은 최대화 시키고, 임의로 뽑인 negative sample들에 대해서는 P(D=0|w,c) 값을 최대화 시킵니다. 따라서 특정 (w, c) 하나에 대해 objective 함수는 아래와 같이 표현할 수 있습니다.


위의 목적식을 최적화하는 것은 관측된 word-context 쌍은 유사한 embedding 결과를 갖도록하고 관측되지 않은 쌍에 대해서는 멀리 떨어뜨리도록 하는 것과 동일합니다. 일반적으로 SGNS가 정말로 유사한 단어들 간의 내적값을 최대화 하는지에 대한 증명에 대해서 친숙하지는 않지만 직관적으로 유사한 문맥에 등장하는 단어들은 유사한 embedding을 가진다는 것을 알 수 있습니다.
3. SGNS as Implicit Matrix Factorization
SGNS는 단어와 해당 단어의 문맥 모두를 d차원의 공간으로 embedding 시켜 결과적으로 단어, 문맥 행렬 W와 C를 얻습니다. 행렬 W의 row는 일반적으로 NLP task에서 사용되지만 행렬 C는 사용되지 않습니다. 그럼에도 불구하고 W행렬과 C^T의 곱행렬인 M을 고려하는 것은 충분히 도움이 될 수 있습니다. 이런 시각으로 보았을 때 SGNS는 |V_w| * |V_c| 차원을 갖는 implicit matrix M을 2개의 행렬로 분해하는 과정으로 생각할 수 있습니다.
행렬 원소 M_ij는 W_i와 C_j의 내적값과 관련이 있습니다. 따라서 SGNS는 row는 단어 w와 관련이 있고, column은 문맥 c와 관련이 있으며 각 원소는 단어-문맥 쌍 사이의 연관 정도를 반영하는 특정 함수값을 내포하고 있는 행렬을 분해합니다.
3.1 Characterizaing the Implicit Matrix
vector w-와 vector c-의 내적은 각 쌍마다 독립이라고 가정할 수 있습니다. 해당 조건 하에서, objective function은 독립적인 vector w-와vector c-의 내적값의 함수로 생각할 수 있으며 objective function을 최대화 하는 값을 찾을 수 있습니다.


3.2 Weighted Matrix Factorization
SGNS의 목적이 모든 (w,c) 쌍들에 대해 PMI(w,c)-logk 값을 통해 최적화 된다는 것을 얻었습니다. vector w-와 vector c-의 차원이 충분히 크지 않을 때는 문제가 발생할 수 있습니다. SGNS의 목적은 지금부터 더욱 자주 등장하는 (w,c) 쌍에 가중치에 더 높게 준 M^PMI - log k 행렬의 최적 d차원 factorization을 찾는 weighted matrix factorization으로 생각할 수 있습니다.
3.3 Pointwise Mutual Information
PMI는 서로 다른 결과 x, y 사이의 연관성을 측정하는 지표입니다.
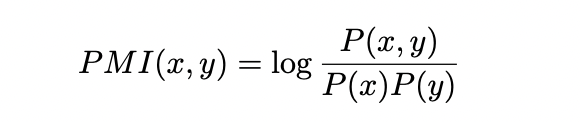
해당 논문에서는 PMI(w,c)는 단어 w와 문맥 c의 joint probability와 각각의 marginal probability의 비율에 log를 취해 연관성을 측정합니다.
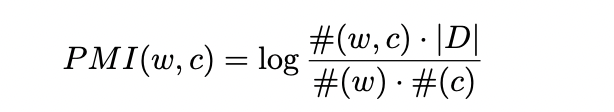
(w,c) 쌍이 존재하지 않을 때는 PMI(w,c)=log0=-inf 가 되는 문제가 발생합니다. 하나의 해결방법은 count matirx에 매우 작은 값의 fake count를 추가하여 확률값을 smooth해줍니다.
또 다른 방법은 아래와 같이 PPMI를 사용하는 것입니다.
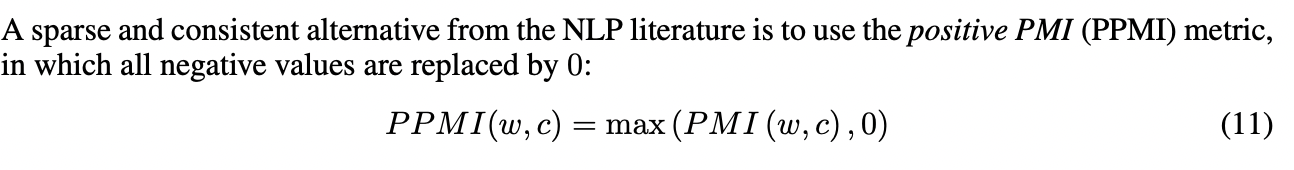
4. Alternative Word Representations
k=1인 SGNS는 M^PMI 행렬을 분해하는 시도이기 때문에, 단어 유사도를 계산할 때 M^PPMI의 row를 직접적으로 활용할 수 있습니다. PPMI는 PMI 행렬의 근사치일지라도 여전히 최적값과 매우 가까운 결과를 얻을 수 있습니다. 해당 section에서는 M^PPMI를 기반으로하는 2가지 word representation 대안을 소개합니다.
4.1 Shifted PPMI
PMI 행렬이 k=1인 SGNS로부터 등장했지만 1이 아닌 다른 값의 k일 때 embedding 결과가 좋다는 것이 알려져 있습니다. k>1 일때 연관성을 측정하는 지표(행렬 원소값)는 PMI(w,c) - logk 입니다. 이는 Shifted PPMI(SPPMI)를 활용할 것을 유도합니다.
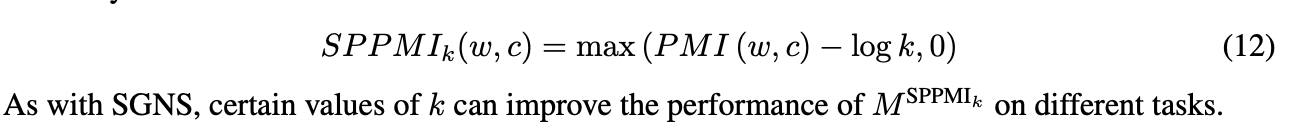
4.2 Spectral Dimensionality Reduction: SVD over Shifted PPMI
sparse vector의 성능이 좋더라도, 낮은 차원의 dense vector가 계산 효율성, 쉬운 일반화 측면에서 장점을 지니기도 합니다. SGNS의 stochasitc gradient training의 alternative matrix factorization은 truncated SVD입니다.

Symmetric SVD

SVD versus SGNS
Spectral algorithm은 stochastic gradient training에 비해 2가지 계산상 이점이 있습니다.
첫째, 정확하고, learning rates와 같은 hyperparameter tuning이 필요하지 않습니다.
둘째, count-aggregated data에서 학습이 쉽습니다.
반대로 stochastic gradient method 역시 장점을 갖습니다.
첫째, 관측된 데이터와 관측되지 않은 데이터를 구분할 수 있습니다. SVD는 관측되지 않은 값에 대해 어려움을 갖고 있습니다.
둘째, SGNS의 objective는 (w,c) 쌍마다 다른 가중치를 부여하고 있습니다.
SGNS와 SVD의 중간 특징을 지니는 방식은 SMF(stochastic matirx factorization)입니다. SVD와 달리 정확하지 않고, hyperparameter tuning이 필요하지만 관측되지 않은 데이터를 다룰 수 있으며 weight를 서로 다르게 부여할 수 있습니다. SMF는 SVD와 유사하면서 SGNS의 절차와는 다르게 aggregated (w,c)에 대해서 작업을 할 수 있으며 말뭉치의 크기가 클 때도 objective가 잘 최적화됩니다. SMF는 SGNS와 SVD의 장점을 모두 갖고 있습니다.
5. Empirical Results
5.1 Optimizing the Objective


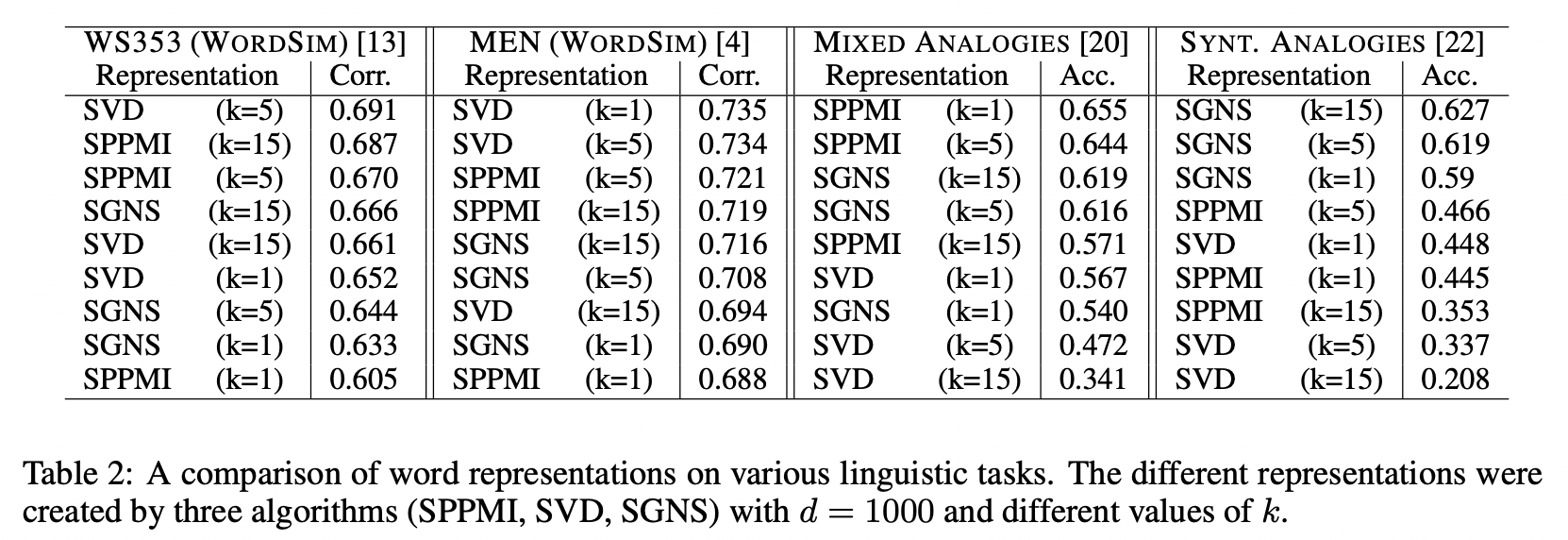
5.2 Performance of Word Representations of Linguistic Task
6. Conclusion
해당 논문에서는 SGNS word embeding algorithm을 분석하고, 해당 방법이 implicitly factorizing the (shifted) word-context PMI matrix (M^PMI - logk)라는 것을 보였습니다. 논문에서는 이론적 발견에서 야기된 PPMI의 수정 버전인 SPPMI을 소개합니다. 실제로 SPPMI를 사용하면 PPMI 행렬보다 성능이 좋았습니다. SPPMI가 SGNS의 objective보다 더 나은 solution일지라도 NLP task에서 항상 SGNS보다 더 나은 성능을 보이는 것은 아니었습니다. 이는 SGNS가 자주 등장하지 않는 단어에는 낮은 가중치를 부여할 수 있기 떄문입니다.