이 글은 부스트캠프 AI Tech 3기 강의를 듣고 정리한 글입니다.
경사하강법에 대해
미분
미분의 간단한 정의와 경사하강법에서 왜 미분이 필요한지 아라보자!
미분의 정의
미분(differentiation) 은 변수의 움직임에 따른 함수 값의 변화를 측정하기 위한 도구로 최적화에서 많이 사용
변화율의 극한으로 정의 한다 ( 접선에서의 기울기 )
미분 by python
import sympy as sym
from sympy.abc import x
sym.diff(sym.poly(x**2 + 2*x + 3), x)
미분의 쓰임새
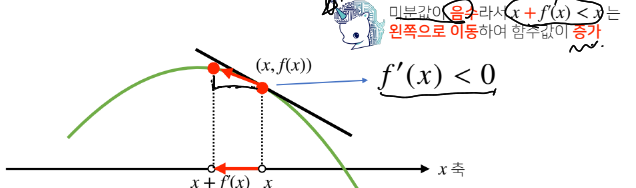
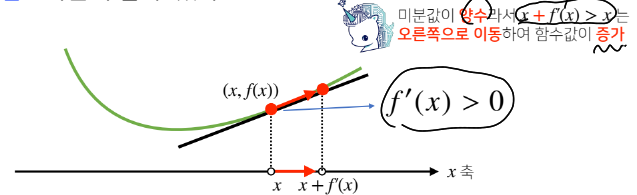
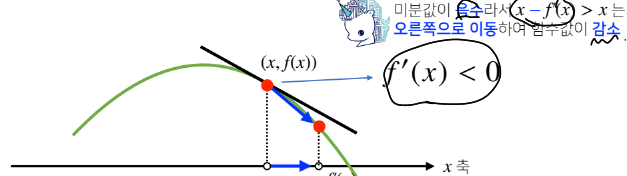
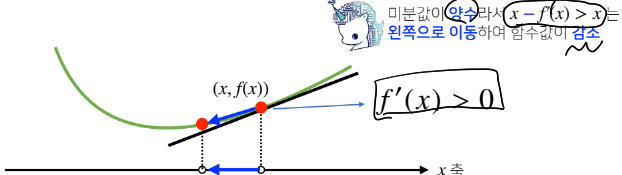
한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가/감소하는지 알 수있다.
x에 미분한 값을 더하거나 뺴주면 항상 f(x)의 값을 증가시키거나 감소시킨다.
경사 상승법
미분값을 더하면 극대값의 위치를 알 수 있다.
목적함수f(x)를 최대화
경사하강법
미분값을 뺴면 극솟값의 위치를 알 수 있다.
목적함수f(x)를 최소화
경사하강법
기본적인 알고리즘
종료조건으로 기울기(grad)가 eps(작은 임의의 값)보다 작을 때 종료
x - lr*f'(x) 를 통해 미분할 var을 업데이트한다.
변수가 벡터라면?
다변수함수의 경우 편미분(partial differentiation) 사용
편미분은 각 변수마다 미분을 해주는 것
각 변수별로 편미분을 계산하여 그레디언트 벡터 만듦(역삼각형은 nabla)
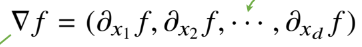
이 그레디언트 벡터를 사용하면 동시에 모든 변수를 동시에 업데이트 가능하다.
그레디언트 벡터로 경사하강법 알고리즘
벡터이기 때문에 기울기의 norm으로 대체하는 것 빼고 동일하다.
(단 L2-norm을 써야하는데, 잔차가 L1-norm(멘하튼거리)일리 없으니 당연하다)
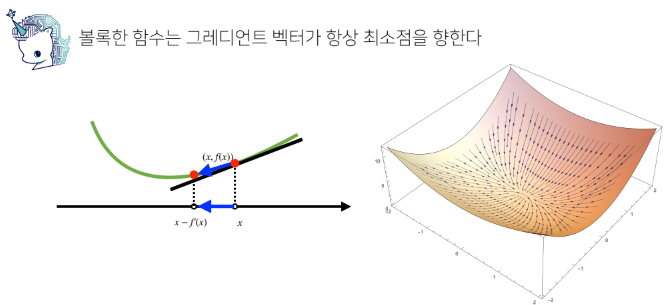
경사하강법에서의 목적식
y:참값 / XB:추정값(y햇 역할)
최소화해야하는 목적식은 참값에서 추정값을 뺀 크기로 베타(B)를 찾아야 한다.
이떄 L2-norm의 제곱을 써도 괜춘하다.
경사하강법 기반 선형회귀 알고리즘
종료조건을 일정학습횟수로 변경한 것을 뺴면 앞에서 쓴 알고리즘과 동일하다.
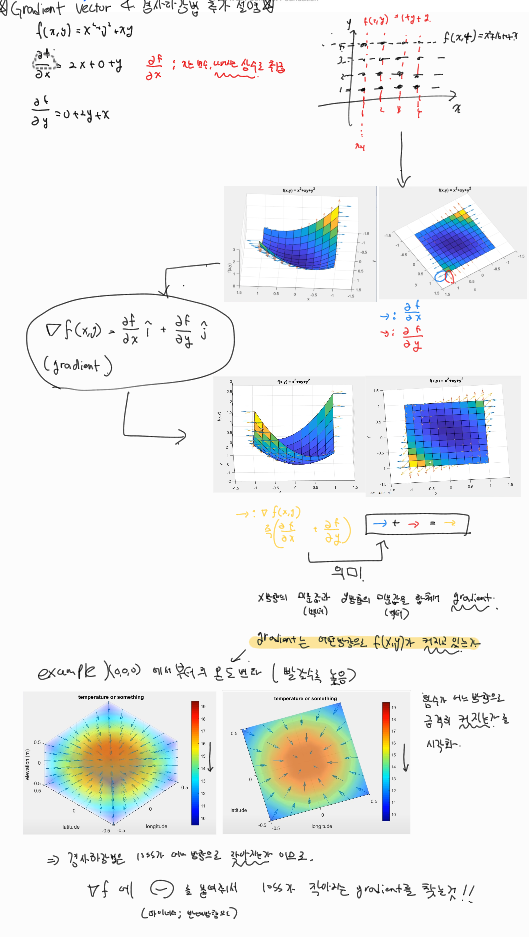
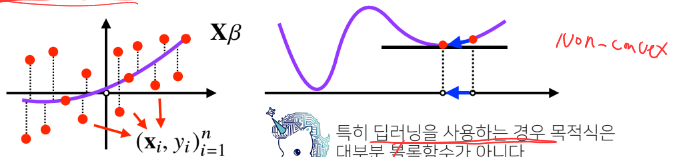
이론적으로 경사하강법은 미분가능&convex(볼록)한 함수에 대해서
적절한 학습률과 학습횟수를 선택 했을 때 수렴이 보장됨
하지만 Non-linear한 경우 목적식이 Non-convex 할 수 있기 때문에 최소값으로의 수렴이 항상 보장X
SGD 확률적 경사 하강법
정의
모든 데이터를 사용하여 업데이트 하는 것이 아닌 데이터 한개(SGD) or 일부활용(미니배치SGD)로 기울기 업데이트
- SGD가 만능은 아니지만 모든 데이터를 사용하는 경사하강법보다 실증적으로 더 낫다.
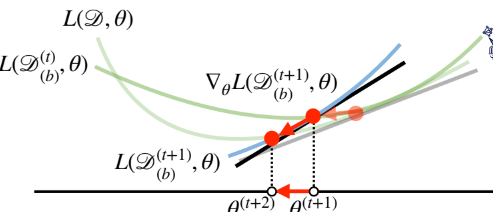
미니배치 SGD
- 데이터의 일부(X_b,Y_b)를 가지고 parameter를 업데이트함
- 연산자원을 효울적으로 활용 가능
전체 데이터를 쓰지않고 미니배치(X_b,Y_b)를 써서 업데이트 하므로 연산량이 b/n으로 감소 - non-convex 목적식은 SGD로 가능
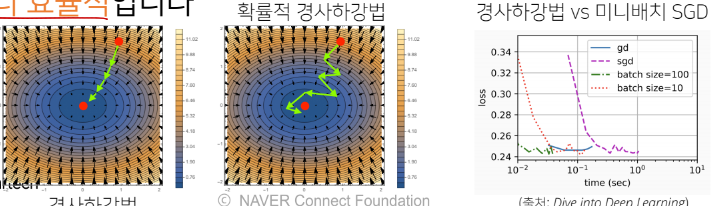
- 확률적으로 선택된 데이터의 일부를 가지고 그레디언트 벡터를 계산하기 때문에 다른 미니배치 사용시 곡선 모양이 바뀌게 됨
3개의 댓글
You have supported me with an interesting amount of knowledge, pizza tower I will bookmark and follow you for more.
The information is well written fnaf. Will benefit anyone who uses it, including me. Keep up the good work. Will definitely be reviewing more posts every day. retro games
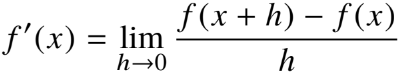

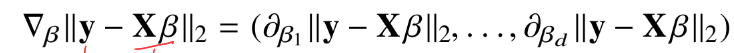




당신이 공유하는 지식은 Mini Crossword 매우 유용합니다. 나는이 지식을 연구하고 찾는 것을 좋아합니다