부분합이란
주어진 수열의 일부 항을 더한 합
→ 수열의 첫 n항까지의 합을 구하는 것이 주된 요소다.
예시를 통해 그 활용을 알아보자.
수열 A = {10, 50, 30, 40, 70, 25, 60} 이라고 하자.
수열의 3번 항부터 5번 항까지의 평균을 구하려면 (30 + 40 + 70)/3을 하면 된다.
만약 2번 항부터 5번 항까지의 평균을 구하려면 (50 + 30 + 40 + 70)/4를 하면 된다.
이런 계산이 빈번해지면 한 번 계산마다 7번씩(최대 N번)을 반복하는 비효율적인 계산이 된다.
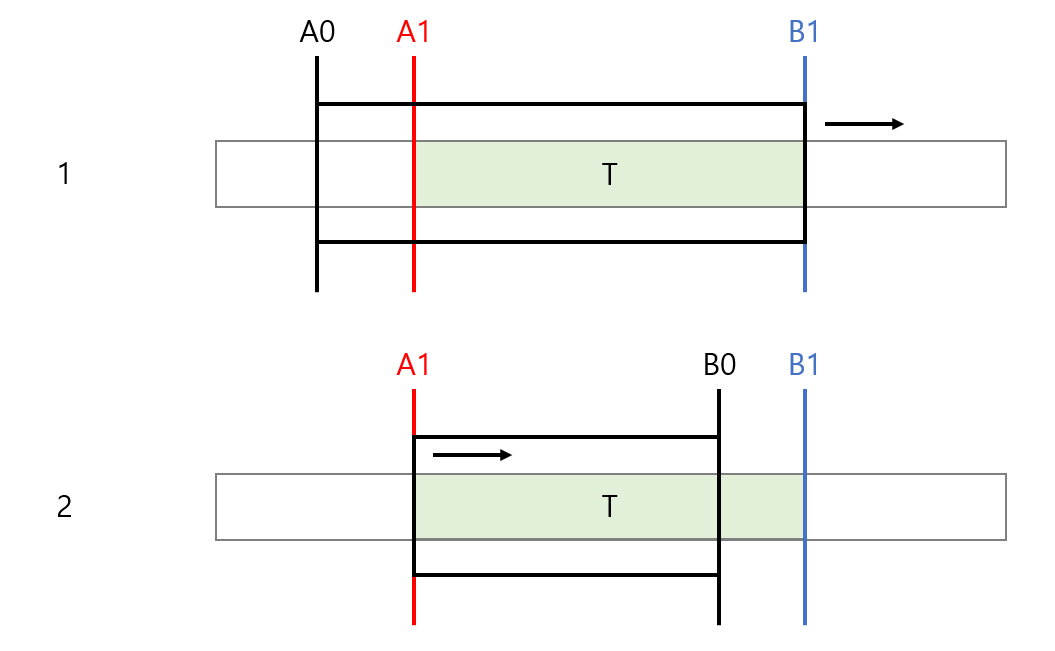
이럴 때 사용하는 것이 부분합 알고리즘이다.
수열의 첫 n항까지의 합, 부분합 Sn을 미리 구해두고 계산하면 훨씬 빠르게 계산할 수 있다.
예를 들어, 2번 항부터 4번 항까지의 평균을 구하려면 S4 - S1을 해주면 된다.
이 때, 2 pointers를 사용하면 O(N)의 시간복잡도로 효율적인 계산이 가능하다.
cf. 2차원 누적합
위의 개념을 2차원으로 확장해보자.
배열의 좌측 상단을 a(1,1)이라고 할 때, S(i, j) = a(1,1)부터 a(i,j)까지의 직사각형이다.

우선 2차원 누적합 배열을 만들어보자.
행 방향으로 누적합을 구하고, 행 누적합에 대해서 열 방향으로 누적합을 구한다.
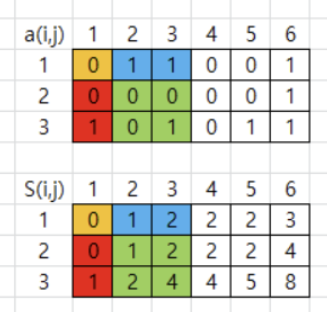
초록색 구간의 누적합을 구하면, S(3,3) - S(1,3) - S(3,1) + S(1,1)이 된다.
-> 2차원 배열의 누적합은 S(x2, y2) - S(x1, y2) - S(x2, y1) + S(x1, y1)으로 계산할 수 있다.
문제
수열의 부분합이 S 이상이 되는 부분합 중에서 가장 짧은 것의 길이를 구하라.
조건
| 0.5 sec | 128 MB |
|---|
- 10,000 이하의 자연수로 이뤄진 수열
- 수열의 길이 N (10 ≤ N < 100,000)
- 수열의 합의 하한 S (0 < S ≤ 100,000,000)
예제
풀이
- 부분합을 모두 구한다.
- 부분합이 S 이상인 구간 중에서 값을 빼보며 여전히 부분합이 S 이상인지 확인한다.
- S 이상이면 최단 길이를 업데이트한다.
- S 미만이면 포인터를 옮겨서 더 탐색한다.
- 부분합이 S 이상이면서 가장 짧은 구간을 찾는다.
코드
N, S = map(int, input().split())
nums = list(map(int, input().split()))
# 2-pointers
f = r = -1
prf_sum = 0
min_len = N+1
while f <= r and r < N: # 10^5
# 현재까지의 합이 S에 못 미칠 경우, 계속 탐색
if prf_sum < S:
r += 1
if r == N:
break
prf_sum += nums[r]
else: # prf_sum >= S: # 합을 넘어선 경우
f += 1
prf_sum -= nums[f] # 앞의 값 제외
min_len = min(r-f+1, min_len) # 최소 길이 계산
result = 0 if min_len == N+1 else min_len
print(result)- prefix sum, two pointer
참고 자료
부분합
2차원 누적합
Test cases
