[BOJ 15686 - 치킨 배달]

kiraMe·2025년 5월 20일

Algorithm_BOJ 다시 풀 문제

Algorithm

목록 보기

8/11

백트래킹이란

모든 경우의 수를 시도하면서 조건을 만족하지 않으면 탐색을 취소하며 불필요한 탐색을 줄이는 기법 (가지치기)

→ “일단 가서 안되면 되돌아간다.”

따라서 DFS 기반이지만 조건 판단하는 과정이 하나 더 있다고 보면 된다.
결국 BruteForce (완전탐색)의 최적화 버전이라고 볼 수도 있다.

주로 언제 사용되냐?

모든 조합, 순열을 탐색할 경우
조건에 맞는 해를 구하는 경우 (N-Queen, 부분집합, 스도쿠, 미로찾기 등)

문제

BOJ 15686 - 문제 보기

요약

치킨집 중 최대 M개만 남기고 나머지를 폐업시킬 때, 도시의 치킨 거리의 최솟값은?

도시 맵 (NxN): 빈칸(0), 집(1), 치킨집(2)

치킨 거리: 한 집에서 가장 가까운 치킨집까지의 거리 (맨해튼 거리 |x1-x2| + |y1-y2| )

도시의 치킨 거리: 모든 집의 치킨 거리 합

조건

1 sec	512 MB

2≤N≤50, 1≤M≤13
1≤집의 개수≤2N, M≤치킨집의 개수≤13

예제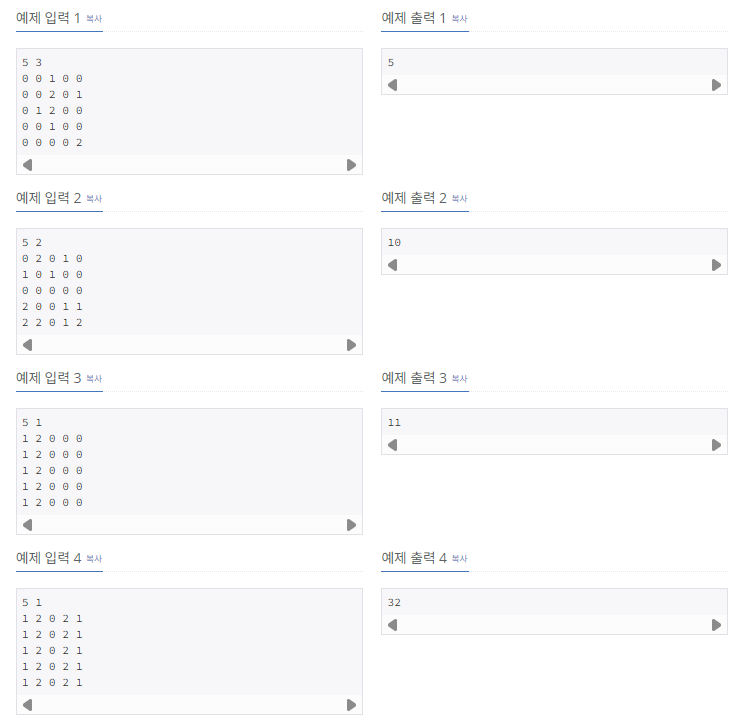

풀이

접근방식

aprch1.
- 각각의 치킨거리를 구하기 each_chicken_dist_map
- 모든 경우 계산해 비교
- dfs/bfs
aprch2. (adopted ✅)
- M개의 치킨집 선택 -> "조합"
- M개의 치킨집을 뽑고, 최소치킨거리합을 구하며 가장 작은 최소치킨거리합을 구함
- dfs, next_permutation/combinations, backtracking

코드

# [1] input
N, M = map(int, input().split())
city_map = [list(map(int, input().split())) for _ in range(N)]
# = [list(map(int, sys.stdin.readline().split())) for _ in range N]


# [2] solution

# 1. 집, 치킨집 위치 구하기 (거리계산용)
house_list = []
chicken_list = []

for r in range(N): # 50
    for c in range(N): # 50
        if city_map[r][c] == 1: # 집 발견
            house_list.append([r, c])
        elif city_map[r][c] == 2: # 치킨집 발견
            chicken_list.append([r, c])

# 2. 치킨집 중에서 M개의 치킨집 선택하기
INF = 1e9 # float('inf')
min_city_chicken_dist = INF

# 2-1
# 최소 도시치킨거리를 찾는 메소드
def find_min_city_chicken_dist():

    global min_city_chicken_dist

    sum_min_dist = 0
    for hx, hy in house_list: # 특정 집에서
        
        min_dist = INF
        for i in survived_chicken_list: # (남은 치킨집들 중)
            
            cx, cy = chicken_list[i] # 특정 치킨집까지의
            dist = abs(hx-cx) + abs(hy-cy)
            min_dist = min(min_dist, dist) # 최소거리 (== 집별치킨거리)

        sum_min_dist += min_dist #의 합 (== 도시치킨거리)
    
    min_city_chicken_dist = min(min_city_chicken_dist, sum_min_dist) # 도시치킨거리 중 최소값

    return

# 2-1. survived_chicken_list를 전역 변수로 사용
survived_chicken_list = [] # 선택된 치킨집 수

def back_tracking(i, cnt): #현재 치킨집 인덱스, 지금까지 선택한 치킨집 수
    
    # M개를 선택완료한 경우:
    if cnt == M:
        find_min_city_chicken_dist() # 최소값 갱신 (조합 찾을 때마다 즉시 갱신함)
        return

    # 인덱스 초과 방지 조건
    if i >= len(chicken_list): 
        return
    
    # 아직 M개를 다 선택하지 못했을 때: 
    # - 현재 치킨집을 선택할 경우
    survived_chicken_list.append(i)
    back_tracking(i+1, cnt+1)
    # 
    # - 현재 치킨집을 선택 취소할 경우 (선택하지 않은 경우, 개수 늘리지 않고 다음으로 이동만)
    survived_chicken_list.pop()
    back_tracking(i+1, cnt)

    return 

# 2-2
# 최소 도시치킨거리를 찾는 메소드
def find_min_city_chicken_dist_with_visited():

    global min_city_chicken_dist

    sum_min_dist = 0
    for hx, hy in house_list: # 특정 집에서
        
        min_dist = INF
        for i in range(len(chicken_list)): # (치킨집들 중)
            if visited[i]: # (선택한 치킨집이라면)

                cx, cy = chicken_list[i] # 특정 치킨집까지의
                dist = abs(hx-cx) + abs(hy-cy)
                min_dist = min(min_dist, dist) # 최소거리 (== 집별치킨거리)

        sum_min_dist += min_dist #의 합 (== 도시치킨거리)
    
    min_city_chicken_dist = min(min_city_chicken_dist, sum_min_dist) # 도시치킨거리 중 최소값

    return

# 2-2. 또다른 풀이: 선택한 치킨집을 visited로 관리
# 굳이 리스트를 만들지 않고, 거리만 계산하기 위함
visited = [False] * len(chicken_list)

def dfs(i, cnt):

    # M개를 선택완료한 경우:
    if cnt == M:
        find_min_city_chicken_dist_with_visited() # 최소값 갱신 (조합 찾을 때마다 즉시 갱신함)
        return
    
    # visited 체크
    for rc in range(i, len(chicken_list)):

        # 아직 방문하지 않은 치킨집이면 선택
        if not visited[rc]:
            visited[rc] = True

            # 이동
            dfs(rc+1, cnt+1)

            # 백트래킹: 원상 복구 (선택 취소)
            # 조합을 만들어내야하기 때문에 
            # 완성한 이후에는 다시 복구해줘야 새로운 조합을 더 찾을 수 있음
            visited[rc] = False

# 2-3. 또다른 풀이: itertools.combinations 이용
# combinations(iterable, r): r짜리 모든 조합 반환 (사전순 정렬 순서로)
# 조합의 개수 = nCr = n!/(r!*(n-r)!)
# 문제의 최대 치킨집 수 <= 13이므로 최대 13C6 (=1716)
from itertools import combinations

def comb():

    global min_city_chicken_dist
    
    # 치킨집 M개 조합 생성
    for chicken_comb in combinations(chicken_list, M):

        # 조합 중 도시치킨거리가 가장 작은 값을 찾음
        sum_min_dist = 0
        for hx, hy in house_list:

            dist = min(abs(hx - cx) + abs(hy - cy) for cx, cy in chicken_comb)
            sum_min_dist += dist

        min_city_chicken_dist = min(min_city_chicken_dist, sum_min_dist)

# [3] output
back_tracking(0, 0) # 또는 dfs(0, 0) # 또는 comb()
print(min_city_chicken_dist)


### cf. 스터디에서 멤버분이 공유한 방법 중에 
# 치킨집에서 집까지의 거리를 계산해서 bfs로 푸는 방식이 있었다.