[BOJ 1525 - 퍼즐]

문제

문제 보러가기: BOJ 1525

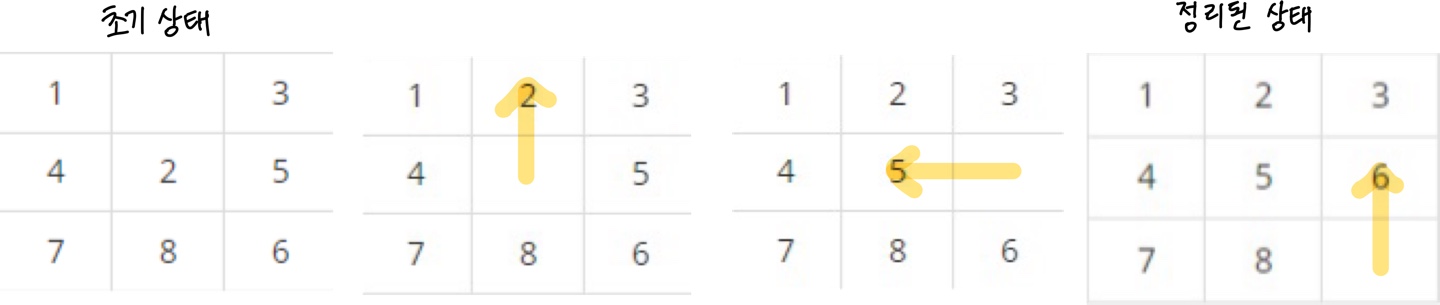
3×3 표에 다음과 같이 수가 채워져 있다.
비어있는 칸이 있으면 인접한 수를 그 칸으로 옮길 수 있다.
정리된 상태로 바꾸려면 몇 번의 최소 이동이 필요할까?

조건

• 빈칸은 0으로 주어진다.
• 정리된 상태로 이동이 불가하면 -1을 출력한다.

예제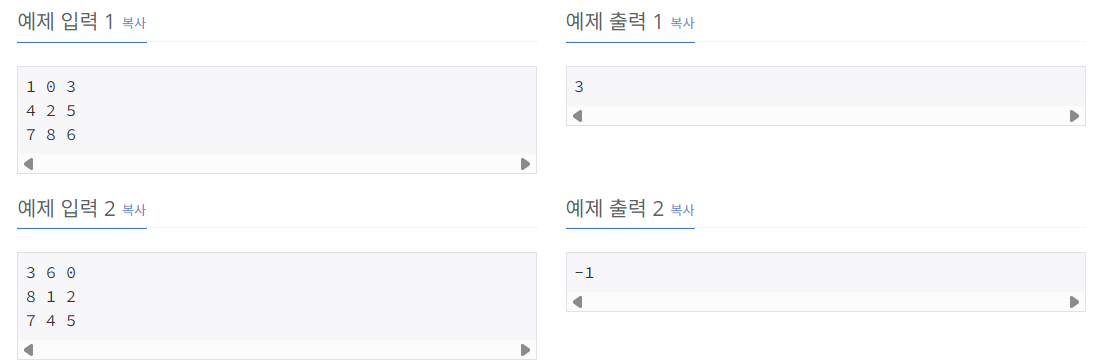

풀이

접근

주어진 2차원 배열을 하나의 문자열로 생각하고 계산하는 것이 핵심이다.

예제 1을 예로 들어보자.

주어진 2차원 배열을 "103425786"과 같은 문자열로 생각하고, 빈칸(0)과 인접한 숫자들과 위치를 바꾸면서 "123456780"에 도달할 수 있는지, 가능하다면 몇 번에 가능한 지를 세면 된다.

이렇게 2차원 배열을 문자열로 바꿔 생각할 땐 주의할 점이 인덱스 계산인데, 2차원 배열의 어떤 행과 열을 각각 x, y라고 할 때 3*x + y가 바로 문자열에서의 인덱스가 된다. 따라서 반대로 문자열에서 행과 열을 계산할 땐, x = idx//3, y = idx%3 이 될 것이다.

현재 0의 인덱스를 (문자열 -> 2차원 배열로) 변환했다면, 인접한 행과 열을 얻는다.
다시 인접한 행과 열을 (2차원 배열 -> 문자열로) 변환해 위치 인덱스를 얻는다.
모두 0과 위치 인덱스를 바꿔줘서 새로운 문자열들을 만든다.

해당 문자열을 이미 검증했는지를 체크하고, 아니라면 Queue에 넣어 다시 정답과 비교해 종료하거나, 다음 문자열들을 계속 만들어 탐색하는 과정을 Queue에 요소가 전부 사라질 때까지 반복하면 된다.

코드

# input
import sys

input = sys.stdin.readline
puzzle = ""
for _ in range(3):
    puzzle += ''.join(input().split()) 


# bfs
from collections import deque

visited = set([puzzle])
que = deque([(puzzle, 0)])

dx = [1, -1, 0, 0]
dy = [0, 0, 1, -1]

ans = -1

while que:

    cur, cnt = que.popleft()

    # escape
    if cur == "123456780":
        ans = cnt
        break
    
    # index of 0 (as arr)
    idx = cur.index("0")
    x, y = idx // 3, idx % 3

    # keep searching
    for i in range(4):

        nx = x + dx[i]
        ny = y + dy[i]

        if nx < 0 or nx >= 3 or ny < 0 or ny >= 3:
            continue  
        
        # swap
        temp = list(cur)
        nidx = nx * 3 + ny
        temp[nidx], temp[idx] = temp[idx], temp[nidx]
        next = ''.join(temp)

        # check visited
        if next in visited:
            continue
        else:
            visited.add(next)
            que.append((next, cnt + 1))


# output
print(ans)

---

• 참고자료
• bfs, graph, hashmap
• Self-feedback
  - 2차원일 때 1차원으로 생각해볼 수 있어야 한다
  - 굳이 인덱스를 계속 비교하는 것보다 1차원 문자열을 숫자로 계산하는 게 더 효율적일지도.. 도전해보기
  - 가능한 수를 한 턴마다 체크해보면서 값을 얻는 건 bfs다. bfs 사용하는 것도 연습 더 많이 하자!