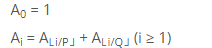[BOJ 1351 - 무한 수열]

문제

문제 보러가기: BOJ 1351

다음 무한 수열 A에 대해서
N, P, Q가 주어질 때, AN을 구하는 프로그램을 작성하시오.

조건

• 0 ≤ N ≤ 10^12
• 2 ≤ P, Q ≤ 10^9
• ⌊x⌋는 x를 넘지 않는 가장 큰 정수 (예를 들어, ⌊1⌋=1이지만 ⌊0.5⌋=0이다.)

예제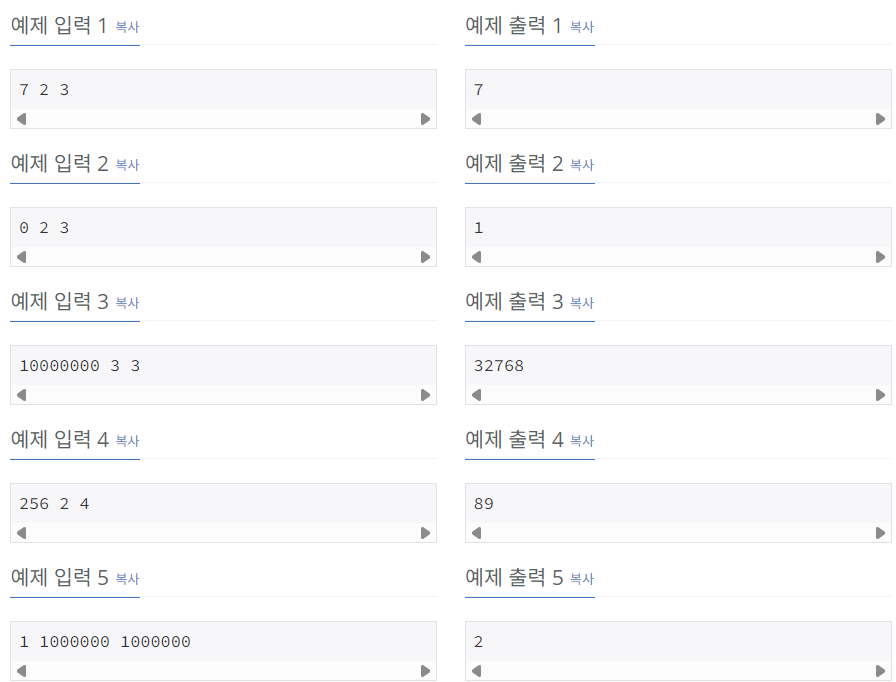

풀이

접근

1. 처음엔 "A[i]를 재귀적으로 계산한다"만을 고려해봤다.

def A(i):

    if i == 0:
        return 1

    return A(i//P) + A(i//Q)

그런데 이렇게 하면 i가 N일 때부터 0이 될 때까지 무조건 계산을 재귀 수행해야하는데 N은 최악의 경우 10^12이기 때문에 시간 초과가 날 수 있다.

2. 따라서 "중복호출 방지를 위해 A[i]를 저장하면서 재귀적으로 계산한다"를 생각해봐야 한다.
   그래서 1차원 dp 배열을 만들어두고 계산마다 저장을 해줘서 이미 계산된 값은 다시 재귀 호출하지 않도록 코드를 만들 수 있다.

dp = [-1] * (N+1)

def A(i):

    if i == 0:
        return 1
    
    pi = i//P
    if dp[pi] == -1:
        dp[pi] = A(i//P)

    qi = i//Q
    if dp[qi] == -1:
        dp[qi] = A(i//Q)
    
    return dp[pi] + dp[qi] 

그런데 이런 방법에서는 1차원 배열을 미리 만들어둬야 한다.
이 문제에서 N은 최악의 경우 10^12이고 메모리 제한은 128MB이기 때문에 메모리 초과가 날 수 있다. (int가 4Byte이므로 128MB면 대략 32,000,000Byte(32MB)개의 정수를 저장할 수 있는데, 32 * 10^6 < 10^12이므로 모든 수를 담지 못한다.)

3. 따라서 "배열이 아닌 Hash로 A[i]를 저장하면서 재귀적으로 계산한다"라는 사실을 알 수 있다.
   python에서 dict()를 사용해 현재 i와 A[i]를 각각 key와 value로 저장하면서, 해시에 없는 i에 대해서만 재귀를 수행하면 시간복잡도와 공간복잡도를 모두 고려한 코드를 짤 수 있다.
   최종 코드는 아래에서 확인할 수 있다.

코드

import sys
input = sys.stdin.readline
N, P, Q = map(int, input().split())

d = dict()

def A(i):

    if i == 0:
        return 1
    
    pi = i//P
    if pi not in d:
        d[pi] = A(i//P)

    qi = i//Q
    if qi not in d:
        d[qi] = A(i//Q)
    
    return d[pi] + d[qi] 

print(A(N))

---

• recursion, dp, hashmap
• self-feedback
  재귀 -> 시간복잡도를 고려하니, DP -> 공간복잡도를 고려하니, Hash
  처음부터 바로 떠올리긴 어려워도 이런 과정이 빠르게 진행되면 좋을 듯하다.