[ICLR 2020]Your Classifier is Secretly An Energy Based Model And You Should Treat It Like One

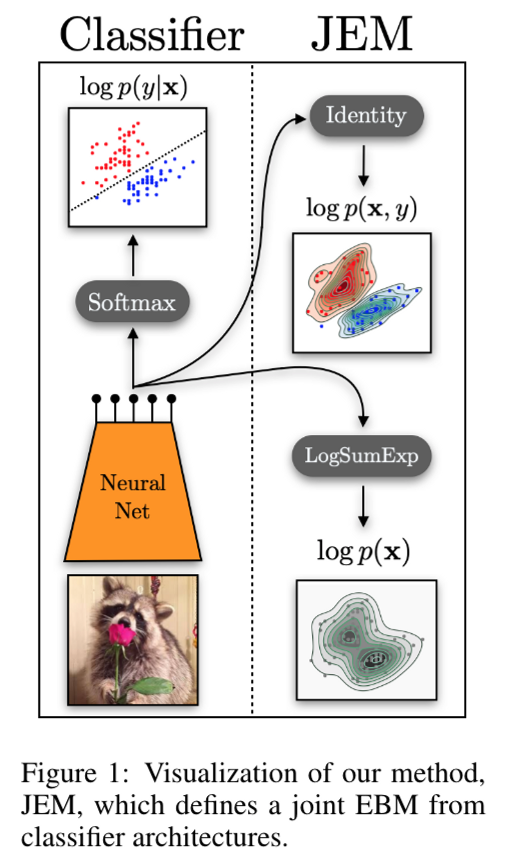
JEM (Joint Energy-Based Models)

Your Classifier Is Secretly an Energy-Based Model and You Should Treat It Like One

---

논문의 주요 내용

이 논문은 표준 분류 모델 $p(y|\mathbf{x})$를 joint distribution $p(\mathbf{x}, y)$ 관점에서 Energy-Based Model (EBM)으로 재해석하여, discriminative 문제에서 generative 모델의 잠재력을 효과적으로 활용하는 방법을 제안한다.

Generative Model의 배경

• Generative Model은 semi-supervised learning, uncertainty calibration, 결측값 보완(imputation) 등 다양한 downstream tasks에서 유용할 것으로 기대되었다.
• 그러나 대부분의 연구는 샘플 품질(qualitative samples)과 validation set의 log-likelihood에 초점이 맞춰져 있었다.
• SOTA generative 모델은 여전히 discriminative 모델의 성능을 따라가지 못하는 경우가 많다.

이 논문의 제안

• EBM을 사용하여 discriminative 문제와 generative 문제를 효과적으로 결합하는 framework를 제시한다.
• Generative 모델이 제공하는 잠재력을 활용하여 모델의 calibration, OOD detection, adversarial robustness를 개선한다.
• 기존 Hybrid 모델(SOTA)의 성능을 능가하는 것을 실험적으로 보여준다.

---

Energy-Based Models (EBMs)

EBM 정의

EBM은 데이터 $\mathbf{x} \in \mathbb{R}^D$에 대한 확률 밀도 함수 $p(\mathbf{x})$를 다음과 같이 정의한다:

• $E_\theta(\mathbf{x})$: Energy function으로, 데이터를 실수 값(scalar)으로 매핑.
• $Z(\theta) = \int_\mathbf{x} \exp(-E_\theta(\mathbf{x}))$: Partition function 또는 normalizing constant.

특징

1. Energy function $E_\theta$는 어떤 함수 형태로도 parametrize 가능하다.
2. $Z(\theta)$는 계산이 어려워, 일반적인 maximum likelihood estimation (MLE) 방식이 바로 적용되지 않는다.
3. 대신, KL divergence를 최소화하는 방식으로 $p_\theta$를 데이터 분포 $p_d$에 근사화한다:

학습 방법

MLE의 gradient는 다음과 같이 유도된다:

여기서 $p_\theta(\mathbf{x})$의 샘플링이 필요하며, MCMC(Markov Chain Monte Carlo)와 같은 샘플링 방법이 사용된다.
대표적으로 Stochastic Gradient Langevin Dynamics (SGLD)가 활용된다:

---

Classifier와 EBM 간의 연결

일반적인 분류 문제에서는 $f_\theta(\mathbf{x})$가 $K$개의 logit 값을 생성하며, Softmax를 통해 확률 분포를 구한다:

논문은 이를 joint distribution $p_\theta(\mathbf{x}, y)$와 marginal distribution $p_\theta(\mathbf{x})$로 재해석한다.

• Joint Distribution:
  $p_\theta(\mathbf{x}, y) = \frac{\exp(f_\theta(\mathbf{x})[y])}{Z(\theta)}, \quad E_\theta(\mathbf{x}, y) = -f_\theta(\mathbf{x})[y]$
• Marginal Distribution:
  $p_\theta(\mathbf{x}) = \sum_y p_\theta(\mathbf{x}, y) = \frac{\sum_y \exp(f_\theta(\mathbf{x})[y])}{Z(\theta)}$

이를 통해, logits를 사용하여 energy를 정의할 수 있다:

---

JEM (Joint Energy-Based Models)

JEM은 기존의 classifier가 사실상 hidden generative capacity를 갖고 있음을 보여준다.

• Discriminative 모델의 $p_\theta(y|\mathbf{x})$를 기반으로 joint modeling을 수행하며,
• $p_\theta(\mathbf{x}, y)$와 $p_\theta(\mathbf{x})$를 결합하여 모델의 성능을 향상시킨다.

Optimization Objective

JEM의 최적화 목표는 다음과 같다:

이를 기반으로, 다음과 같이 gradient를 계산한다:

Loss 구성 요소

1. Discriminative Term: Cross-entropy loss를 통해 $p_\theta(y|\mathbf{x})$를 최적화.
2. Generative Terms:
   • Negative samples $\mathbf{x}^\prime$에 대해 energy를 증가.
   • Positive samples $\mathbf{x}$에 대해 energy를 감소.

SGLD를 통해 negative samples를 생성하며, generative term이 포함된 joint loss를 최적화한다.

---

결론

1. Joint Modeling Framework: Discriminative와 Generative 모델을 통합하는 새로운 관점을 제안.
2. SOTA 성능 개선: 기존 Hybrid 모델보다 우수한 성능을 보임.
3. Robustness 및 Generalization: Calibration, OOD detection, adversarial robustness에서 개선된 결과를 입증.

JEM은 기존의 classifier가 generative capacity를 내포하고 있음을 증명하며, 이를 통해 discriminative와 generative 문제를 통합적으로 다루는 효과적인 방법을 제시한다.