문제 설명
콜라츠 추측이란 로타르 콜라츠(Lothar Collatz)가 1937년에 제기한 추측으로 모든 자연수 k에 대해 다음 작업을 반복하면 항상 1로 만들 수 있다는 추측입니다.
1-1. 입력된 수가 짝수라면 2로 나눕니다.
1-2. 입력된 수가 홀수라면 3을 곱하고 1을 더합니다.
2.결과로 나온 수가 1보다 크다면 1번 작업을 반복합니다.
예를 들어 주어진 수가 5 라면 5 ⇒ 16 ⇒ 8 ⇒ 4 ⇒2 ⇒ 1 이되어 총 5번만에 1이 됩니다.
수가 커졌다 작아지기를 반복하는 모습이 비구름에서 빗방울이 오르락내리락하며 우박이 되는 모습과 비슷하다고 하여 우박수 또는 우박수열로 불리기도 합니다. 현재 이 추측이 참인지 거짓인지 증명되지 않았지만 약 1해까지의 수에서 반례가 없음이 밝혀져 있습니다.
은지는 우박수열을 좌표 평면 위에 꺾은선 그래프로 나타내보려고 합니다. 초항이 k인 우박수열이 있다면, x = 0일때 y = k이고 다음 우박수는 x = 1에 표시합니다. 이런 식으로 우박수가 1이 될 때까지 점들을 찍고 인접한 점들끼리 직선으로 연결하면 다음과 같이 꺾은선 그래프를 만들 수 있습니다.
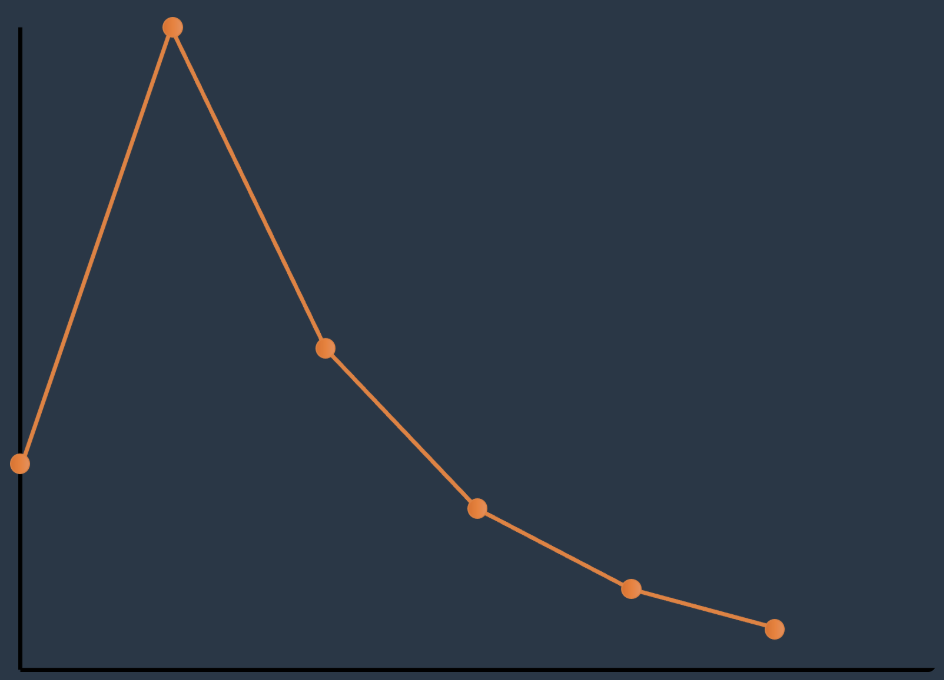
은지는 이렇게 만든 꺾은선 그래프를 정적분 해보고 싶어졌습니다. x에 대한 어떤 범위 [a, b]가 주어진다면 이 범위에 대한 정적분 결과는 꺾은선 그래프와 x = a, x = b, y = 0 으로 둘러 쌓인 공간의 면적과 같습니다. 은지는 이것을 우박수열 정적분이라고 정의하였고 다양한 구간에 대해서 우박수열 정적분을 해보려고 합니다. 0 이상의 수 b에 대해 [a, -b]에 대한 정적분 결과는 x = a, x = n - b, y = 0 으로 둘러 쌓인 공간의 면적으로 정의하며, 이때 n은 k가 초항인 우박수열이 1이 될때 까지의 횟수를 의미합니다.
예를 들어, 5를 초항으로 하는 우박수열은 5 ⇒ 16 ⇒ 8 ⇒ 4 ⇒ 2 ⇒ 1 입니다. 이를 좌표 평면으로 옮기면 (0, 5), (1, 16), (2, 8), (3, 4), (4, 2), (5, 1) 에 점이 찍히고 점들을 연결하면 꺾은선 그래프가 나옵니다. 이를 [0,0] 구간에 대해 정적분 한다면 전체 구간에 대한 정적분이며, [1,-2] 구간에 대해 정적분 한다면 1 ≤ x ≤ 3인 구간에 대한 정적분입니다.
우박수의 초항 k와, 정적분을 구하는 구간들의 목록 ranges가 주어졌을 때 정적분의 결과 목록을 return 하도록 solution을 완성해주세요. 단, 주어진 구간의 시작점이 끝점보다 커서 유효하지 않은 구간이 주어질 수 있으며 이때의 정적분 결과는 -1로 정의합니다.
나의 풀이 과정!!
우박수열이란?
콜라츠(Collatz) 추측으로 나온 값들을 그래프로 표현했을 때의 모양이 y값이 커졌다 작아졌다를 반복하는 우박을 닮았다 해서 우박수열이라고 부른다.(어이없...)
정적분은 모자란 내 기억에 의하면 그래프로 표현했을 때 아래로 y=0까지의 면적을 말한다.
다행히 x와 x+1 사이의 그래프는 직선이므로 면적의 크기는 사다리꼴 면적으로 계산하면 간단하다.
문제 이해하기
문제에서 주어진 구간을 정적분하라는건 이해했지만
범위 ranges에 대해서 뭔소린지 이해하기가 어려워 진짜 여러번 읽어봤다...
예를들어 초항 k = 5인 경우, 우박 수열은 5, 16, 8, 4, 2, 1이 되므로 이 때 그래프 직선의 수 n = 5가된다.(각 수열을 잇는 직선의 수)
이 때 int ranges[][] = [[0,0],[0,-1],[2,-3],[3,-3]]가 주어진다면
처음 [0, 0]에서
a = 0이니까 x = 0 좌표에서부터
b = 0이니까 x = 끝에서부터 - 0 좌표 까지의 면적을 의미
다른 예시로 [2, -3] 이라면
a = 2니까 x = 2 좌표에서부터
b = -3이니까 x = 끝에서부터 -3 좌표 까지의 면적을 의미한다.
문제 접근 방법
1.콜라츠 수열을 구하기
2.구간별 면적을 미리 구해놓기
3.각 구간별 면적 값을 구하기
완성 코드
import java.util.ArrayList;
import java.util.List;
public class Test_84_HailSequenceDefiniteIntegral { // 우박수열 정적분
public double[] solution(int k, int[][] ranges) {
// 1.콜라츠 수열을 구하기
List<Integer> collatz = new ArrayList<>();
while (k != 1) {
collatz.add(k);
k = (k % 2 == 0) ? k / 2 : k * 3 + 1;
}
collatz.add(1); // 마지막 값인 1을 추가
int n = collatz.size() - 1; // 선분 개수
// 2.구간별 면적을 미리 구해놓기(사다리꼴 넓이 저장)
double[] areas = new double[n];
for (int i = 0; i < n; i++) {
areas[i] = (collatz.get(i) + collatz.get(i + 1)) / 2.0;
}
// 3.각 구간별 면적 값을 구하기
double[] answer = new double[ranges.length];
for (int i = 0; i < ranges.length; i++) {
int a = ranges[i][0];
int b = ranges[i][1];
int end = n + b;
// 유효하지 않은 구간
if (a > end) {
answer[i] = -1.0;
continue;
}
double sum = 0;
for (int j = a; j < end; j++) {
sum += areas[j];
}
answer[i] = sum;
}
return answer;
}
}문제는 생각보다 어렵지 않았지만
문제를 해석하고 이해하는데에 시간이 많이 소모되었다...
(옛날의 나는 정적분 공부를 어떻게 했더라)
