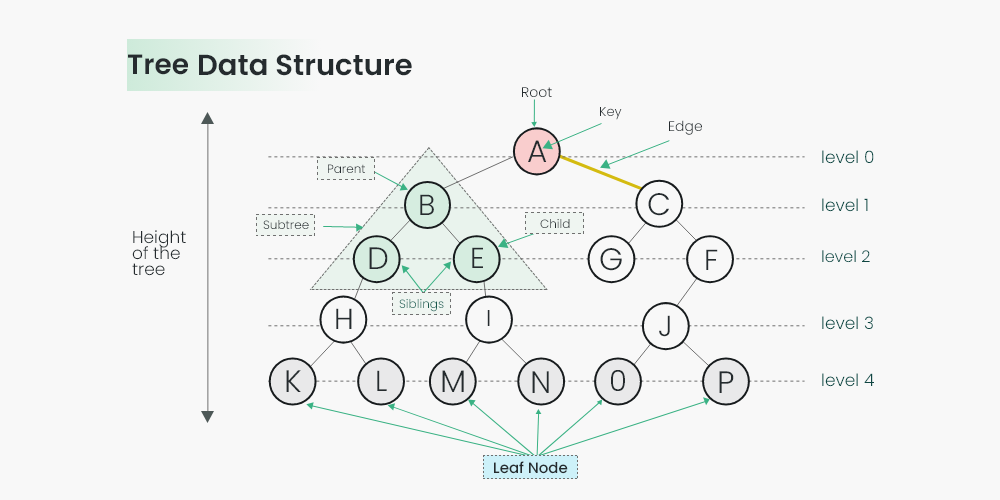
트리
트리는 방향을 가진 그래프. 노드를 가리키는 간선은 단 하나씩.
여러 용어가 존재함.
- 레벨 : 깊이를 의미한다. 위에서부터 0~n level
- 루트 : 맨 위 노드, 시작지점.
- 부모 : 하위노드를 갖고 있는 노드
- 자식 : 상위노드를 갖고있는 노드
- 서브 트리 : 트리 내부의 작은 트리.
- 리프 노드 : 자식이 없는 노드.
- degree : 간선(edge)
규칙도 있다.
- 루트를 제외한 모든 정점은 하나의 부모를 가짐
- 정점이 N개인 트리는 N-1개의 간선을 가짐(도형의 선분 개수)
- 루트에서 특정 정점으로 가는 경로는 하나.
트리는 어디에서 사용할까?
보통 조직도, 파일구조 등.
트리는 여러 종류가 있다.
이진트리
탐색을 위한 트리.
정점이 최대 2개의 자식을 가진다.
- 정점이 N개면 최악의경우 높이가 N
- 정점 N개면 포화or완전이진트리 높이 log N
=> 높이 h인 포화이진트리는 정점이 2^h - 1개 - 이진트리는 보통 완전이진트리로 힙 구현하기위해 쓴다...
완전 이진 트리
마지막 레벨을 제외한 모든 정점이 채워져있음.
왼 => 오 순으로 노드가 차있어야함.
포화 트리
맨밑까지 평평하게 다 채워짐. 모든 리프노드가 동일레벨.
구현
그래프의 일종이여서 그래프처럼 구현 가능.
이진트리는 2개씩있으니, 배열이나 링크드 리스트로 쉽게 가능하다.
const binaryTree = [
1,
5, 6,
3,7,9,8];
//이렇게 표현이 가능하다. 부모는 index/2 - 1, 자식은 왼쪽이면 index*2 + 1, 오른쪽은 index*2 + 2숙제로 전위,중위,후위 순회를 내주셨다. 기간 안에 작성해보겠다.
힙
이진트리에서 설명한 녀석.
이녀석을 설명하기 위해선 우선순위 큐가 필요.
우선순위 큐는 자료구조가 아닌 개념.
우선순위가 높은 원소가 먼저 나감(FIFO가 아님). 왜 큐라고 부를까?
Queue의 정의는 대기줄. 사람들이 알기 쉽게 하기 위해...
개인적으로는 우선순위 힙이 맞아보임ㅋㅋ
- 루트값이 가장 크거나 가장 작다.
- 힙을 이용한 힙정렬(Heap sort)도 있음.
트라이
이녀석도 트리를 이용한 구조. 문자열 저장-탐색에 쓰임
=> 검색어 자동완성에 쓰인다!
저장-탐색이 문자열의 길이만큼 걸림. wow
하지만 각 정점이 자식에 대한 링크를 전부 갖고있어야 하기에, 저장공간 소모가 크다.
- 루트는 공백
- 각 간선(링크)는 추가될 문자를 키로 가짐.
=>taxi면t, ta, tax, taxi - 각 정점은 이전 정점 값 + 간선 키를 값으로 가짐.
- 해시테이블 + 연결 리스트 사용
자동완성 구현 숙제 => 전위순회 써야할듯