https://www.youtube.com/watch?v=2Yi_Jse_7JQ&t=3398s
위 자료를 참고했다.

---

요즘들어 데이콘을 통해 공부를 하는 중인데, catboost 모델이 자주 사용되길래 관련 영상을 찾아 공부해봤다.
내가 이해한대로 정리한거라 오류가 있을 수 있다.

---

Background

Gradient Boosting Model

• Gradient Boosting은 "순차적으로"최적화 함수를 설계해나간다.
  • Bagging과의 차이에 유의
  • $F^t$: $F^{t-1}$+$\alpha h^t$
    - 위 식에서 alpha는 step size, h는 base predictor가 된다.
    - 즉, "누적된 모형"에 현재 시점에서 찾은 모형의 정보를 반영해나가는 것
    - 이때 $h^t$는 Gradient step을 의미하며, expected loss를 최소화하는 방향으로 선택된다.
    
    
• 즉, negative gradient와 현재 h(x) 함수 추정했을 때 그 차이에 대한 expectation이 최소가 되도록 하는 t번째 시점에서의 tree 모형을 만드는 게 Gradient Boosting Model
  • $h^t = \underset{h \in H}{\arg\min}$ $\mathbb{E}{(-g^t (\mathbf{x}, y) - h(\mathbf{x}))^2}$

• XGBoost, LightGBM, CatBoost순으로 나왔다.

기존 Gradient Boosting의 문제점

Prediction Shift

• target값이 존재하는 데이터는 유한함. (학습데이터와 테스트 데이터의 분포 차이)
  • 즉, 학습데이터에만 과도하게 피팅되는 오버피팅의 문제 존재

Target Leakage

• 범주형 데이터를 수치형으로 변환시키기 위해 해당 속성에 타깃값의 평균값을 사용하여 수치형 데이터로 변환하게 되는 문제
  • (학습 과정에서) y가 feature value를 계산하는 데 사용되는 것
  • 즉, 정답 정보가 속성 정보를 정의하는 데 사용됨

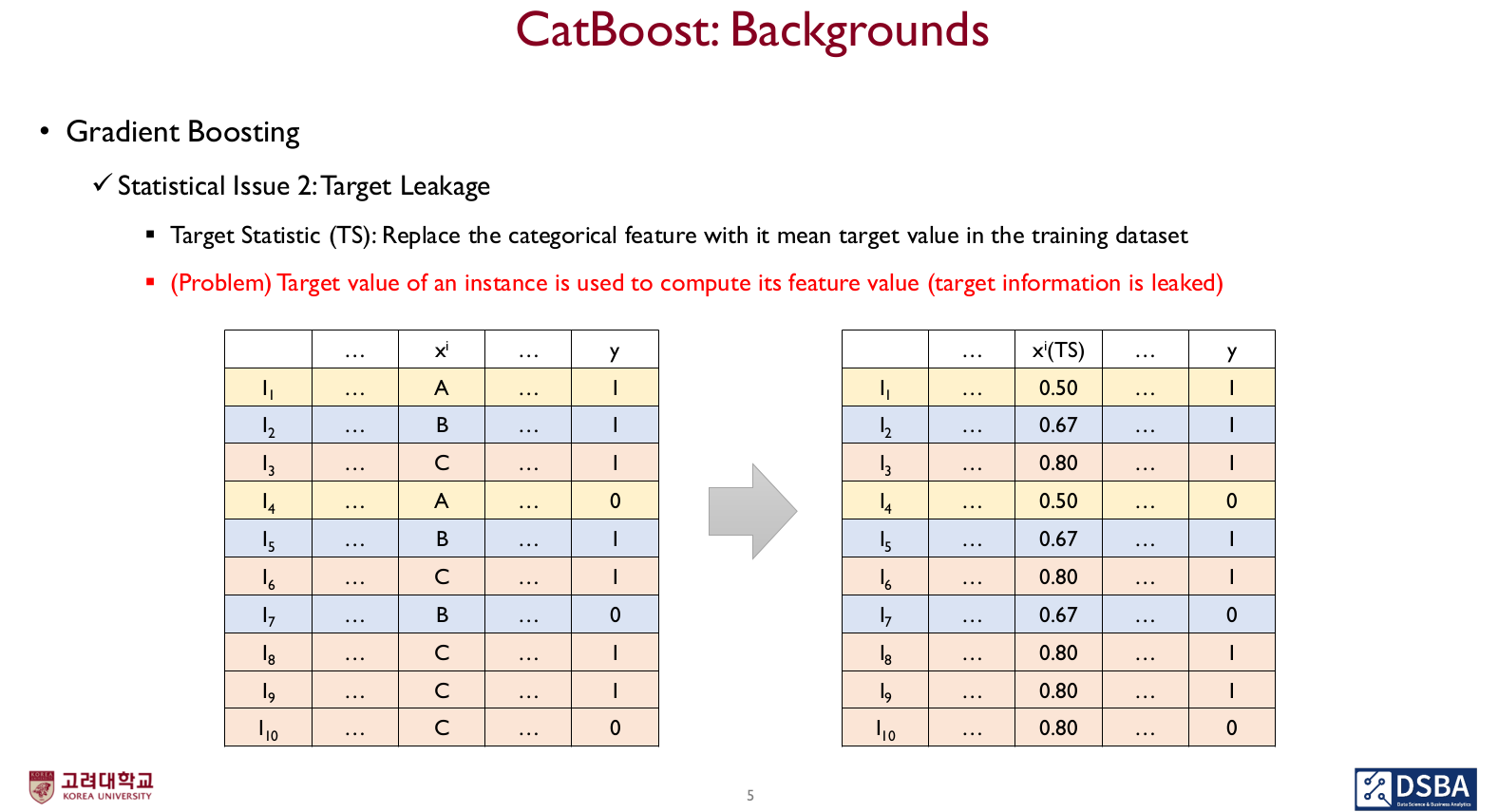
Catboost의 기존 문제 해결 방안

• Target Leakage -> Ordered Target Statistics
• Prediction Shift -> Ordered Boosting

Target Leakage 관련

• 특정 feature value를 게산함에 있어 y값을 안쓰고 어떻게 할 것인가

One hot encoding (dummy 변수 만들어 사용)

• 변수가 너무 많아질 수 있는 문제 존재

Target Statistics

• 기존 카테고리를 그룹핑해서 Target Statistics로 변환하는 방법 (TS)
  • 각 카테고리의 y값의 평균으로 변환 (위에서 본 방법)

Smoothing을 적용한 Greedy TS

• low-frequency의 noisy한 카테고리의 부정적 영향을 줄이기 위함
  

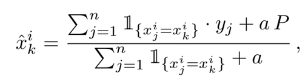
  여기서 a는 파라미터, p는 데이터셋의 평균 target value를 의미(common setting)

  • 예시
    
    
    결국 이런 식으로 변환된다.
    
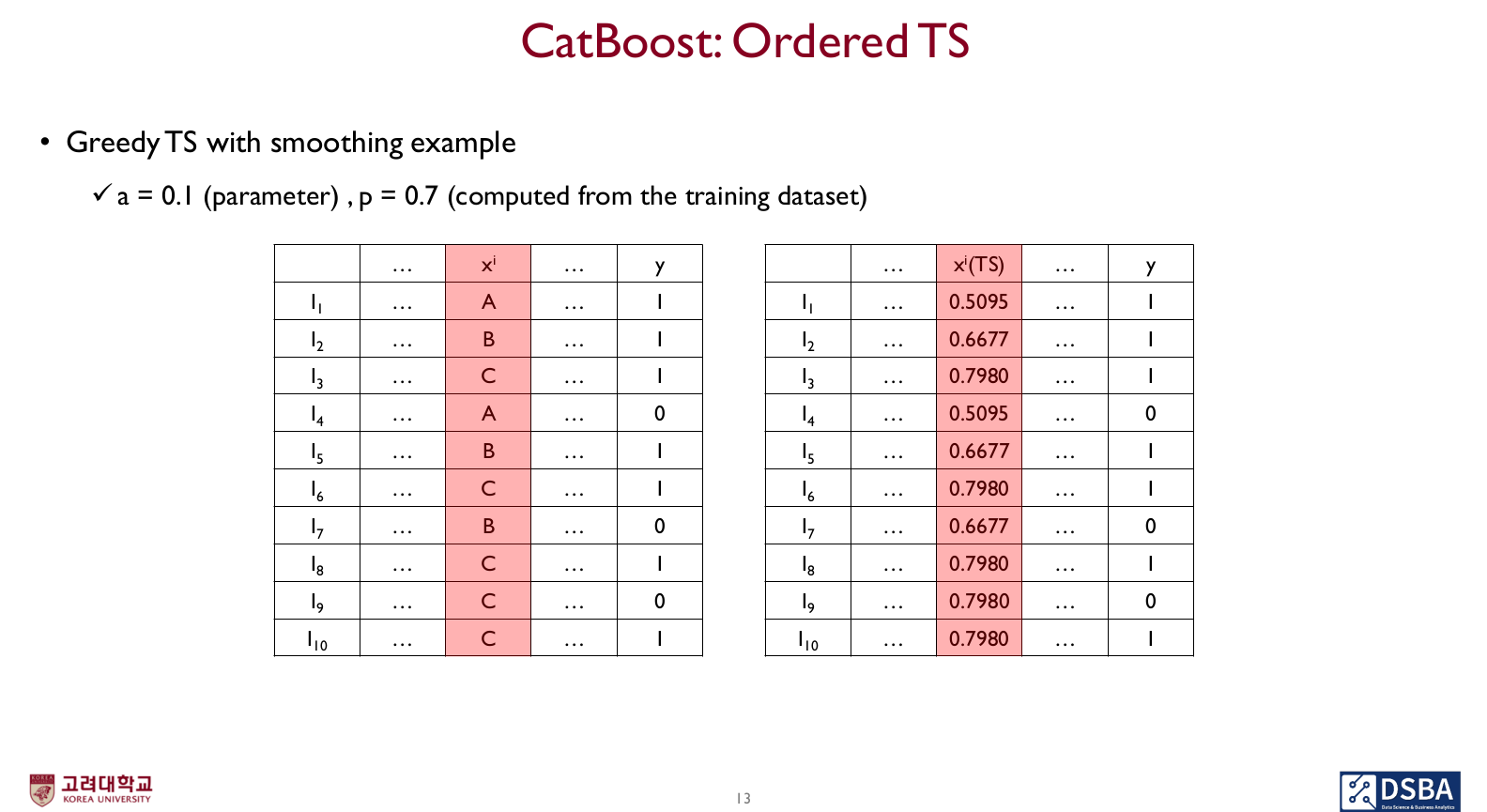
  • 그러나 위 방법들은 모두 학습과정에서 y값을 사용하게 되고, 실제 테스트떄는 y값을 참조하지 못하므로 문제 발생 (Prediction shift 방지)
    • Catboost는 예측값을 계산할 때 위 수식에서의 $y_j$부분을 쓰지 않음

Greedy TS의 약점

• test set의 모든 데이터가 unique한 카테고리 값을 가질 때(training data에서 한 번도 등장 x) test set에 대해서 전혀 구분해내지 못하는 문제
  • test set의 feature value가 p로 통일됨
  • 이 예시에서는 $x_i$변수에 대해 어떠한 split point를 적용해도 구분해낼 수 없음

---

Catboost Idea

Target Statistics가 가져야 할 속성

• 학습 데이터와 테스트 데이터에 대한 expectation이 같아야 한다
  

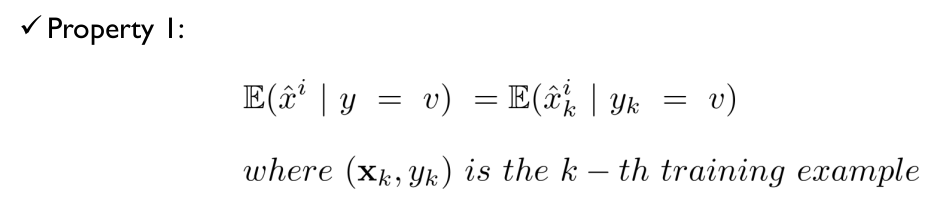
• 가급적이면 TS를 계산함에 있어 모든 데이터를 효과적으로 사용할 것

• cf) Hold-out TS(해당 속성 제외해 학습)은 두 번째 속성 위반
  Leave-one-out TS(하나의 데이터만 제외해 학습)는 Target Leakage 발생

Ordered TS (Ordered Target Statistics)

• 현재 데이터가 시계열 데이터가 아니더라도 가상의 시간 개념을 도입해 random하게 permutation시킴 (artificial time 도입)
  • 현재 객체보다 이전 객체들만 사용해 학습하는 것
    • 그냥 이렇게 하면 첫 번째 객체가 여러 번 사용될 것이기에, random permutation을 사용하는 것
    • 이것이 Ordered TS!
    • 위 TS 속성 두 가지를 모두 만족한다.
      

이런 방식으로 계산해나간다.
이렇게 함으로써 target leakage는 방지된다.

• Prediction Shift 관련
  • I개의 트리에 대해 학습할 때, $F^{I-1}$은 $\mathbf{x_k}$의 example 없이 학습되어 residual $r^{I-1}(\mathbf{x_k}, y_k)$이 unshifted되도록 해야 함
  • 그렇기에 제안하는 것이 Ordered Boosting

Ordered Boosting

• Prediction shift 문제 방지
  • Ordered TS와 마찬가지로 random permutation 사용
    

이런 방식으로 계산된다. 즉, 이전 객체들로만 학습된 모델로 현재 객체와의 residual을 구해나가는 방식이므로 prediction shift 문제가 발생하지 않는다.

• Ordered TS와 Ordered Boosting은 같은 permutation을 사용한다.

---

Catboost Procedure

Initialization

• S+1개의 독립적인 random permutation을 학습데이터로부터 생성
  • s개는 split을 evaluation하는 데 사용되며, 하나는 얻어진 트리의 마지막 leaf value를 계산하는 데 사용됨
    • leaf node를 계산하는 데 있어 이전에 사용한 permutation을 사용하면 안되기 때문
• Ordered boosting을 사용해 계산된 TS와 prediction은 높은 variance를 가짐
  • Permutation 여러 번 반복 필요

Oblivious tree 구축

• Oblivious tree란, 같은 레벨마다 같은 split critetrion을 사용하는 것
  • supporting model $M_{r,j}$를 얻어내는데, $M_{r,j}(i)$는 r번째 permutation에서 j까지의 example로 학습된 모델로 i번째 example에 대해 예측을 한 결과를 말한다.
  • random permutation을 통해 트리를 만들어준다.
  • 각 i example에 대해 gradient를 계산해준다.
  • 이때, candidate splits evaluation step에서는 example i에 대한 leaf value $\Delta(i)$는 이전까지 만들어진 gradient의 평균을 내 계산 (i번째 example이 있는 레벨)

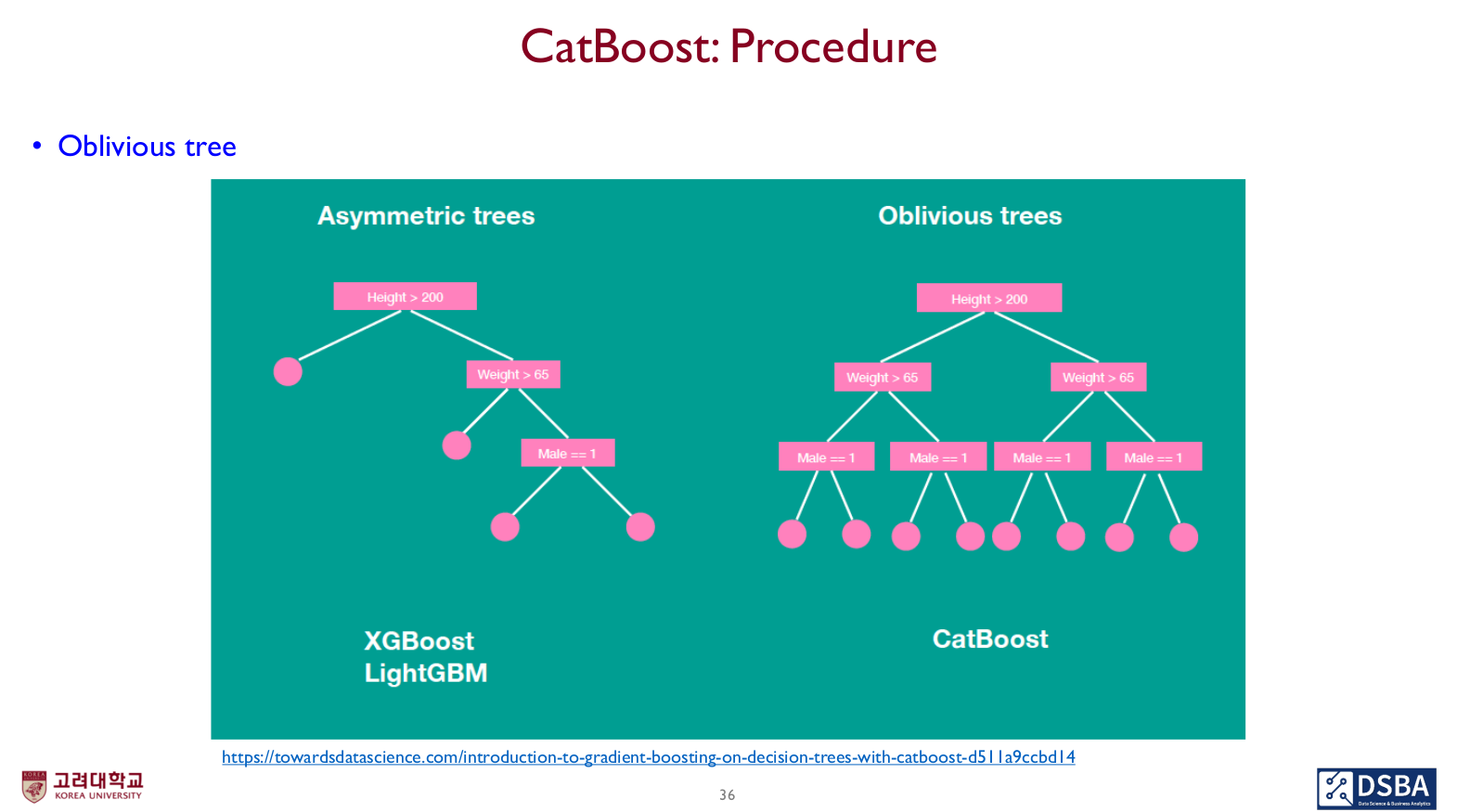
자세한 진행 과정은 영상을 참고하는 게 좋을듯!

선례가 없는 경우, 0으로 값이 초기화되고 있다.


쭉 같은 방식으로 계산되어간다.

최종적으로 candidate split c에 대한 loss는 coscine loss로 계산된다.

이때, 남겨둔 하나의 permutation을 이용해 지금까지 사용한 결과물들을 계산하고, 마지막에 남은 델타가 트리의 leaf node value가 된다.

• 최종 모델 F 가 testing time에 새로운 example에 대해 적용될 떄 TS는 모든 Training data를 사용해 계산된다.
  

---

XGBoost vs. LightGBM vs. CatBoost

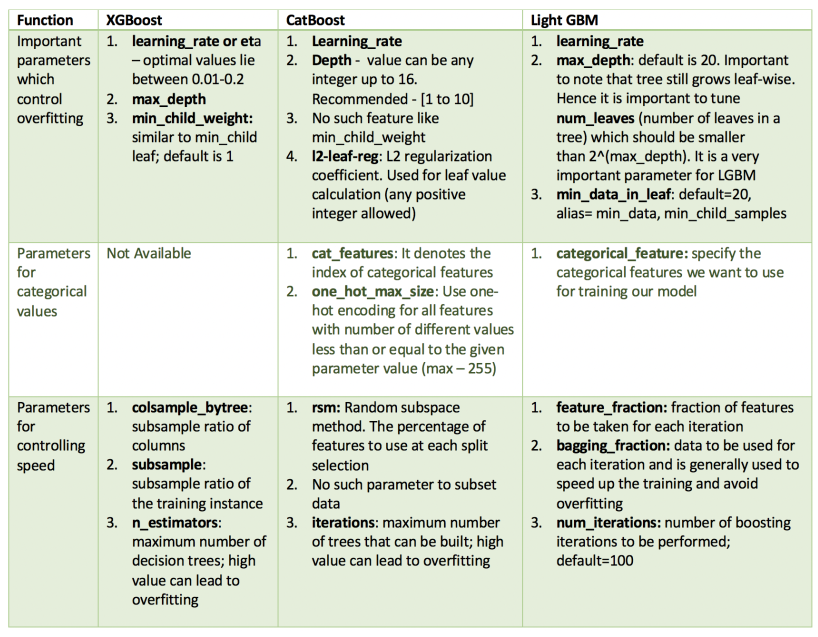
데이터 특성마다 적합한 모델을 선택해주면 될듯하다.

• Catboost의 경우, 범주형 데이터가 존재할 때 사용 (수치형 데이터가 대부분일때 상대적으로 약함)
• LightGBM의 경우, XGBoost보다 알고리즘이 가벼우면서 좋은 성능 낼 수 있지만 적은 데이터에서 Overfitting 위험 (10000개 이하의 데이터 기준)

---

뭔가뭔가 매우 복잡하고 어려웠다 ㅋㅋㅋ
한 번에 이해하기는 어려우니, 자주 보면서 익숙해지도록 하자.